? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
基础知识
向量
概念:有大小和方向的量
基础算法:
(1)加:(A.x+B.x,A.y+B.y)(A.x+B.x,A.y+B.y)(A.x + B.x,A.y + B.y)
(2)减:(A.x−B.x,A.y−B.y)(A.x−B.x,A.y−B.y)(A.x - B.x,A.y - B.y)
(3)乘常数:(A.x∗k,A.y∗k)(A.x∗k,A.y∗k)(A.x k,A.y k)
(4)点积:A⋅B=|A||B|cosθ=A.x∗B.x+A.y∗B.yA·B=|A||B|cosθ=A.x∗B.x+A.y∗B.yA · B = |A||B|\cos\theta = A.x B.x + A.yB.y
(5)叉积:A×B=|A||B|sinθ=A.x∗B.y−A.y∗B.xA×B=|A||B|sinθ=A.x∗B.y−A.y∗B.xA \times B = |A||B|\sin\theta = A.x B.y - A.yB.x
基础算法
(1)旋转:将 (x,y)(x,y)(x,y) 逆时针旋转 θθ\theta 就是 (x∗cosθ−y∗sinθ,x∗sinθ+y∗cosθ)(x∗cosθ−y∗sinθ,x∗sinθ+y∗cosθ)(x \cos\theta - y \sin\theta,x \sin\theta + y \cos\theta)
(2)把向量 AAA 转到与向量 BBB 同向:B∗|A||B|B∗|A||B|B \dfrac{|A|}{|B|}
(3)求多边形面积:12|∑n−1i=1Pi×P(i+1)%n|12|∑i=1n−1Pi×P(i+1)%n|\dfrac{1}{2}|\sum_{i=1}^{n-1}P_i \times P_{(i+1)\%n}|
(4)以 AAA 为原点 BBB 为单位点求 PPP 的新坐标:(AB→⋅AP→,AB→×AP→)∗1|AB|2(AB→·AP→,AB→×AP→)∗1|AB|2(\vec{AB} · \vec{AP},\vec{AB} \times \vec{AP}) \dfrac{1}{|AB|^2}
(5)PPP 与直线 ABABAB 的位置关系:根据 AB→×AP→AB→×AP→\vec{AB} \times \vec{AP}
(6)点 PPP 在直线 ABABAB 上的投影:A+AB→∗(AB→⋅AP→)|AB|2A+AB→∗(AB→·AP→)|AB|2A + \dfrac{\vec{AB} (\vec{AB} · \vec{AP})}{|AB|^2}
(7)点与线段的位置关系:判断与线段所在直线的位置关系、点积判断在哪里
(8)AB//CD:AB→×CD→=0AB//CD:AB→×CD→=0AB \mathop{//} CD:\vec{AB} \times \vec{CD} = 0
(9)直线 ABABAB 和直线 CDCDCD 求交点:A+AB→∗CD→×CA→AB→×CD→A+AB→∗CD→×CA→AB→×CD→A + \vec{AB} \dfrac{\vec{CD}\times\vec{CA}}{\vec{AB} \times \vec{CD}}
(10)线段与直线求交点:线段两端点在直线两侧、直线求交点
凸包
Graham 扫描法
求凸包:
(1)找到所有的点中最左下角的点,并加入栈中
(2)将所有点按极角排序逆时针
(3)每次找到一个点,判断该点是否在最后这条边的右边,若是则弹出栈顶,直到不能弹出就加入栈里
求下凸壳:
按横坐标从小到大排序,然后执行上文 (3)
求上凸壳:
按横坐标从大到小排序,然后执行上文(3)
旋转卡壳
本质:固定一个点,所求与另一个点的位置呈单峰函数且峰值关于固定点单调的算法
例题:
题目描述:
求解凸多边形的直径。直径的定义为凸多边形上两点间距离的最大值。
解法:
(1)任意选择一个点为固定点
(2)以固定点在逆时针顺序下的下一个点为第二个点
(3)因为这两点间的距离与第二个点的位置呈单峰函数,且峰值关于固定点单调,所以就按逆时针方向移动第二个点
(4)移动到最大距离处,计算贡献,并按逆时针方向移动固定点,不移动第二个点
(5)重复(3)直到移动结束
例如下图所示: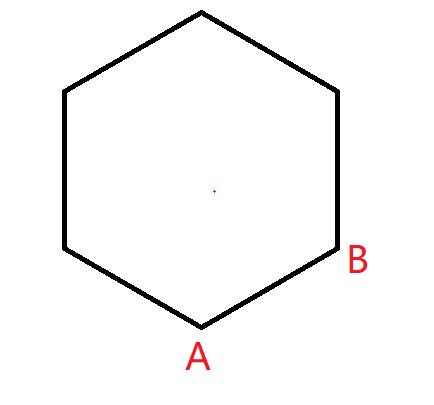
先随机找到固定点 AAA,与对应的第二个点 BBB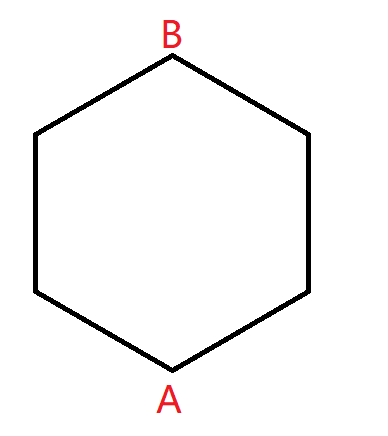
移动 BBB ,使得 AAA 与 BBB 两点间距离最大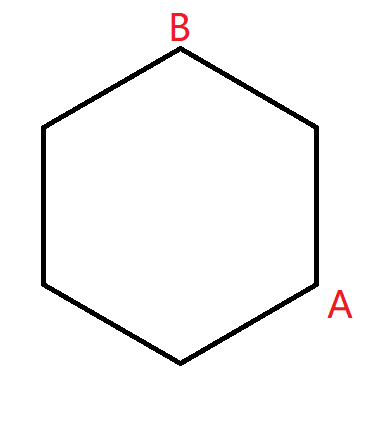
保持 BBB 不动,移动 AAA
然后再按照上文的方法一直循环执行
圆
点与圆
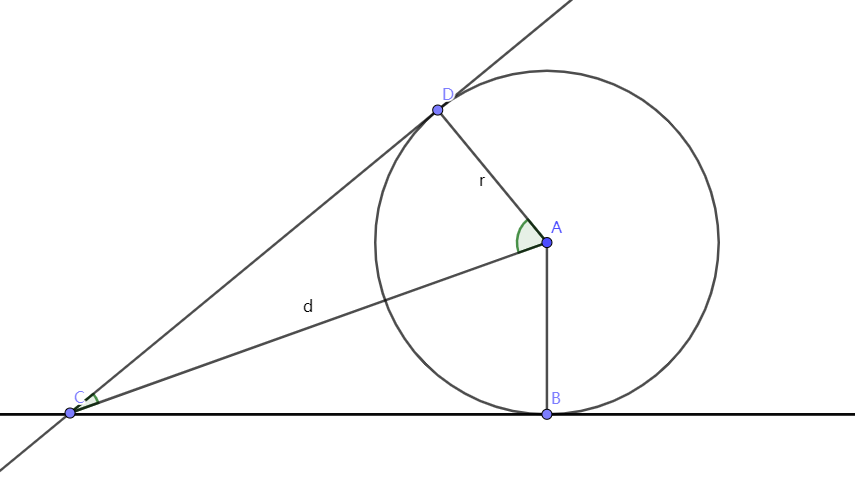
判断点是否在圆上: d≤rd≤rd \le r
d=|PC|,r=rd=|PC|,r=rd = |PC|,r = r ∠DAC=arccos(rd),∠DAC=(arcsinrd)∠DAC=arccos(rd),∠DAC=(arcsinrd)\angle DAC = \arccos(\dfrac{r}{d}),\angle DAC = (\arcsin\dfrac{r}{d})
直线与圆
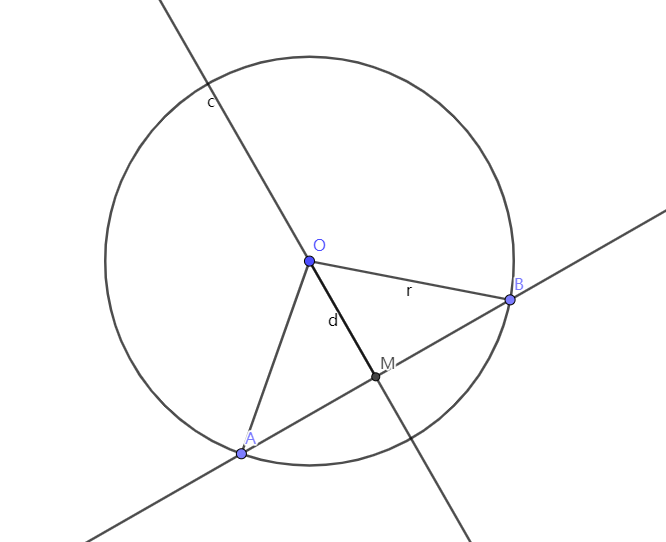
根据叉积得到 ddd
|MA|=|MB|=r2−d2−−−−−−√|MA|=|MB|=r2−d2|MA| = |MB| = \sqrt{r^2 - d^2},∠OBM=arccosdr∠OBM=arccosdr\angle OBM = \arccos \dfrac{d}{r}
圆与圆
是否相交
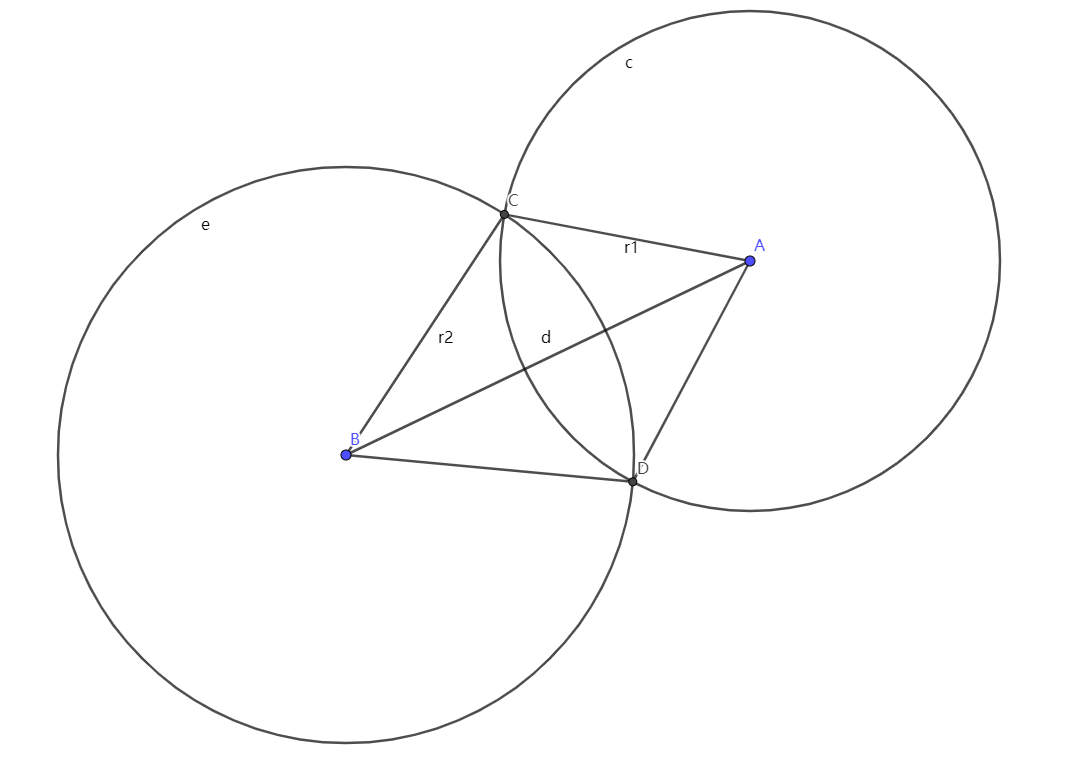
根据 ddd 与 r1+r2r1+r2r_1 + r_2
不交圆外公切线
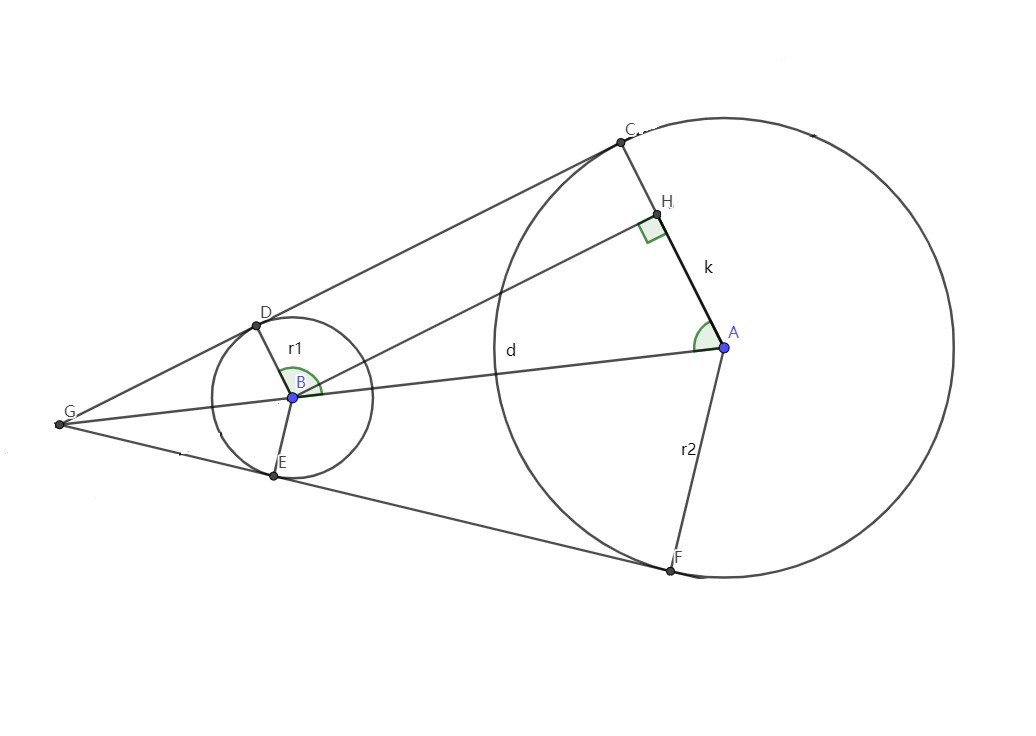
k=r2−r1,∠CAB=arccosr2−r1d,∠DBA=arccosr1−r2dk=r2−r1,∠CAB=arccosr2−r1d,∠DBA=arccosr1−r2dk = r_2 - r_1 , \angle CAB = \arccos \dfrac{r2-r1}{d},\angle DBA = \arccos \dfrac{r_1-r_2}{d}
不交圆内公切线
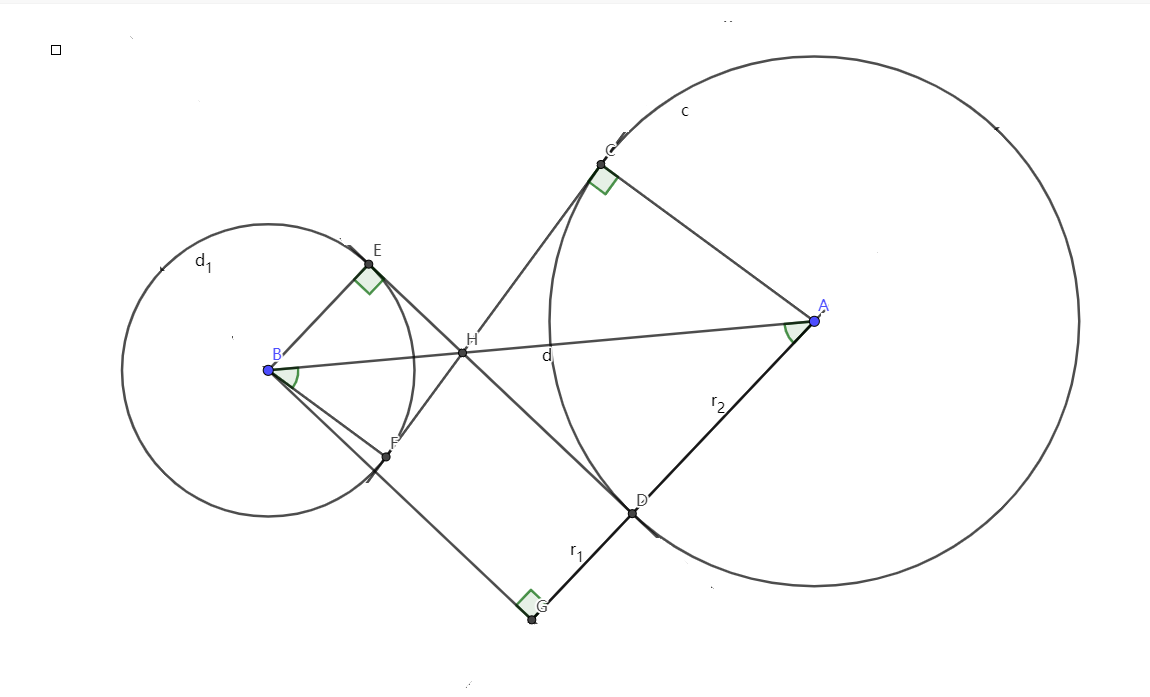
∠BAG=∠ABF=arcsinr1+r2d∠BAG=∠ABF=arcsinr1+r2d\angle BAG = \angle ABF = \arcsin \dfrac{r_1+r_2}{d}
转载请注明:xuhss » 【学习笔记】计算几何