Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475

红黑树

定义

动机：

• 二叉查找树查找、插入、删除最坏情况时间复杂度可能退化为 O(n)。
• AVL 树很好的限制了数的高度为 O(logn)，插入、删除、查找的最坏时间复杂度均为 O(logn)；但删除操作最多需要做 O(logn) 次旋转。

• 红黑树是具有如下特点的二叉查找树：

  • 每个结点是红色或黑色的
  • 根结点为黑色
  • 外结点为黑色（外界点即为 null）
  • 如果一个结点时红色，那么它的孩子必须是黑色
  • 任一结点到外结点的路径上，包含相同数目的黑结点

结点的黑高度：该结点到外结点的路径上包含的黑结点数目

红黑树的黑高度：根结点的黑高度

性质

• 若忽略红结点而只考虑黑结点，则这棵树是平衡的
• 任何一条路径上不能有两个连续的红结点。从任意结点触发最长的路径（红黑结点间隔组成）是最短路径（仅由黑结点组成）的 2 倍
• 任何一个结点的左右子树的高度最多相差 2 倍
• 红黑树的平衡性比 AVL 树更弱
• 平均和最坏高度：O(logn)
• 查找、插入、删除操作的平均和最坏时间复杂度是 O(logn)，且仅涉及 O(1) 次旋转
• 红黑树的高度：h = O(logn) 且 logn <= h <= 2logn
  

结点定义

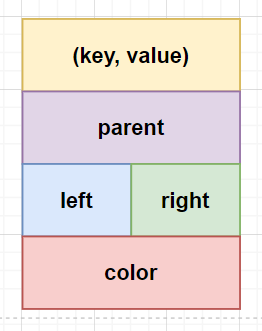
1️⃣ key：关键字的值
2️⃣ value：关键字的存储信息
3️⃣ parent：父亲结点的引用
4️⃣ left：左子树根结点的引用
5️⃣ right：右子树根结点引用
6️⃣ color：结点颜色

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14

java`class RBNodeextends Comparable, V> {
public RBNode parent;
public RBNode left;
public RBNode right;
public boolean color;
public K key;
public V value;

public RBNode(RBNode parent, K key, V value) {
this.parent = parent;
this.key = key;
this.value = value;
}
}`

插入算法

• 查找，若查找成功则不插入并更新结点值；若查找失败，再查找失败的位置插入新结点
• 新结点总是作为叶结点插入的
• 新结点必须为红色
• 若新结点的父结点是黑色，则插入过程结束
• 若新结点的父结点是红色，则需要处理双红缺陷

这里定义 x 为新插入的结点，p 为 x 的父结点，g 为 x 的爷爷结点，u 为 x 的叔叔

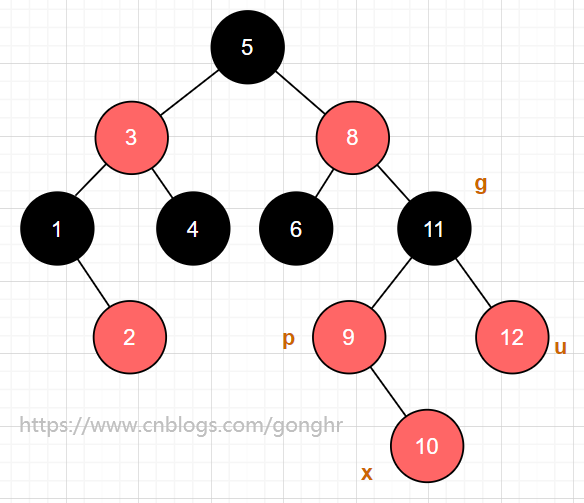
双红修正

1️⃣ x 的叔叔是黑色

• g 到 x 的路径为 LL 型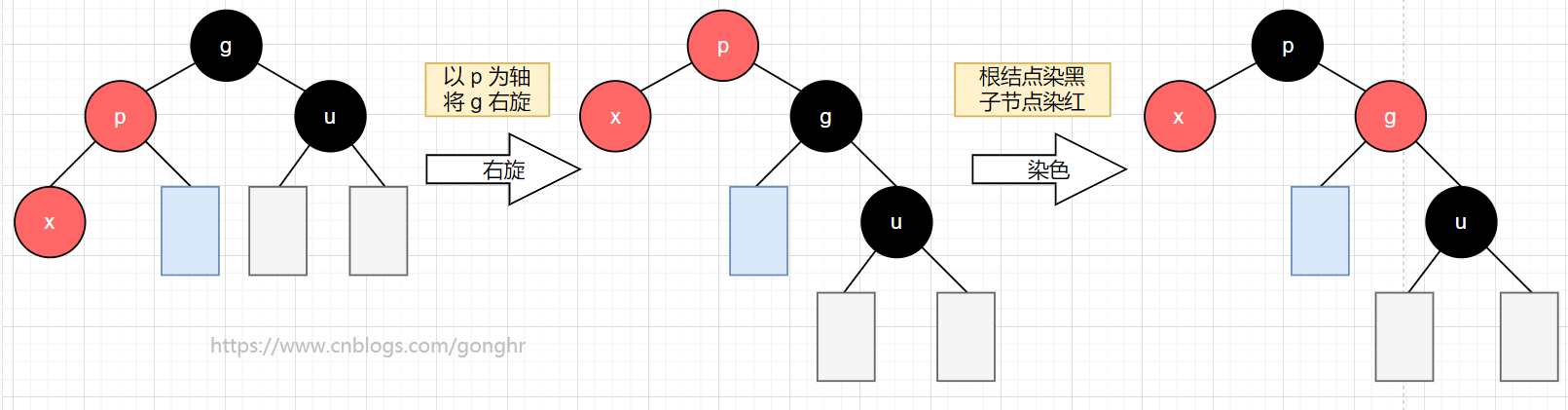
  
• g 到 x 的路径为 RR 型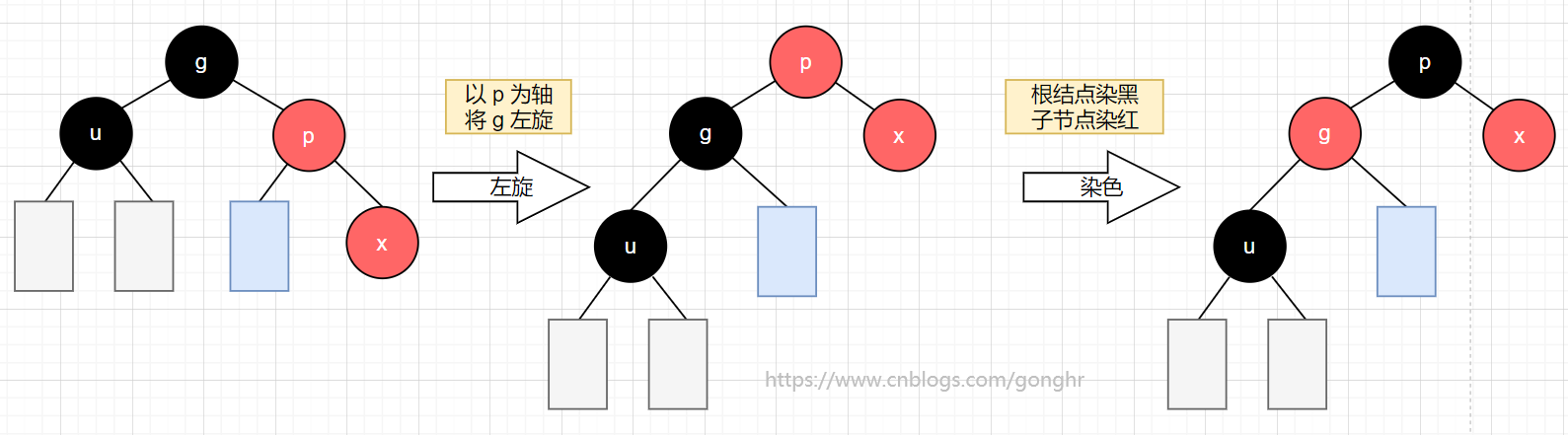
  
• g 到 x 的路径为 LR 型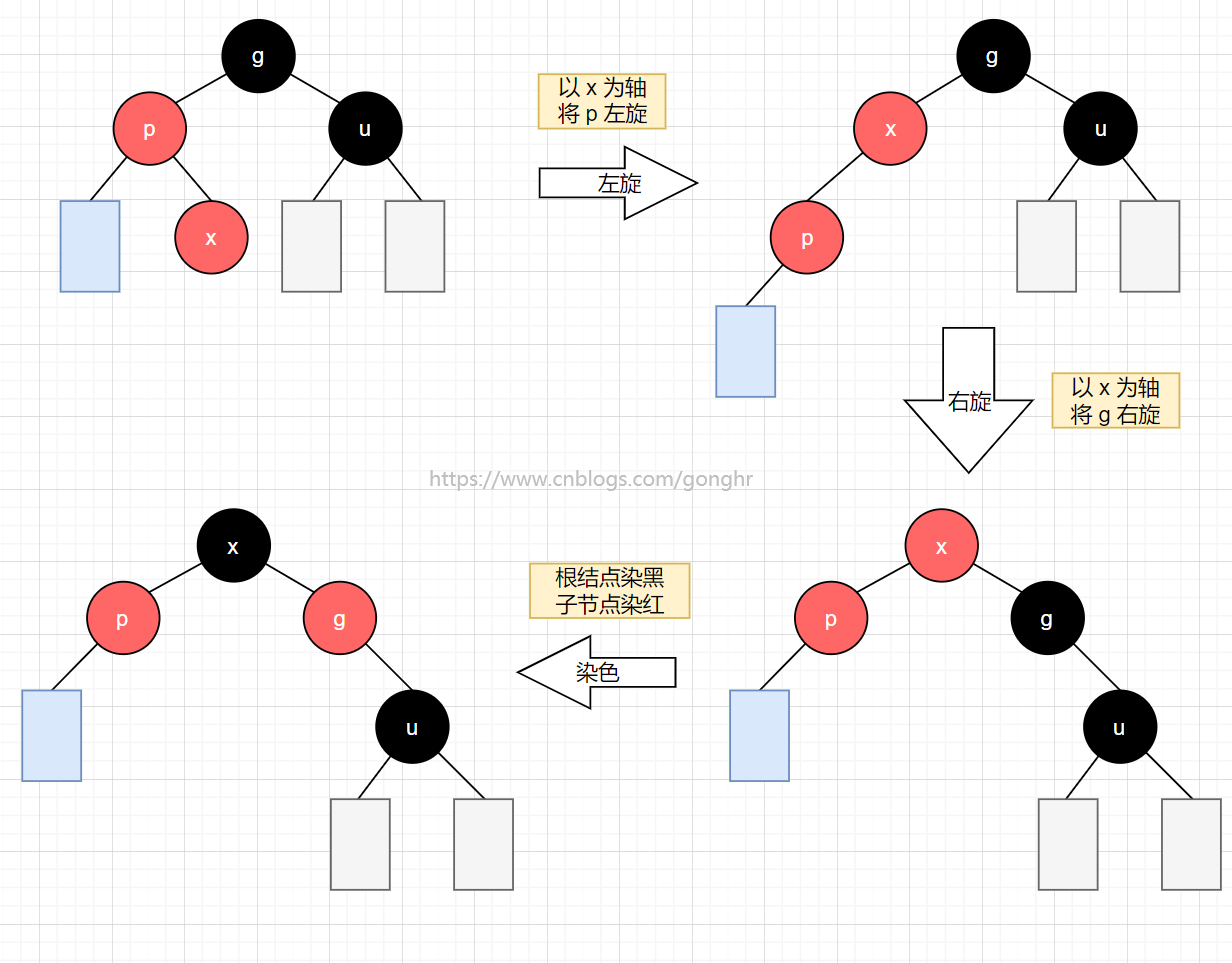
  
• g 到 x 的路径为 RL 型
  

2️⃣ x 的叔叔是红色

实例

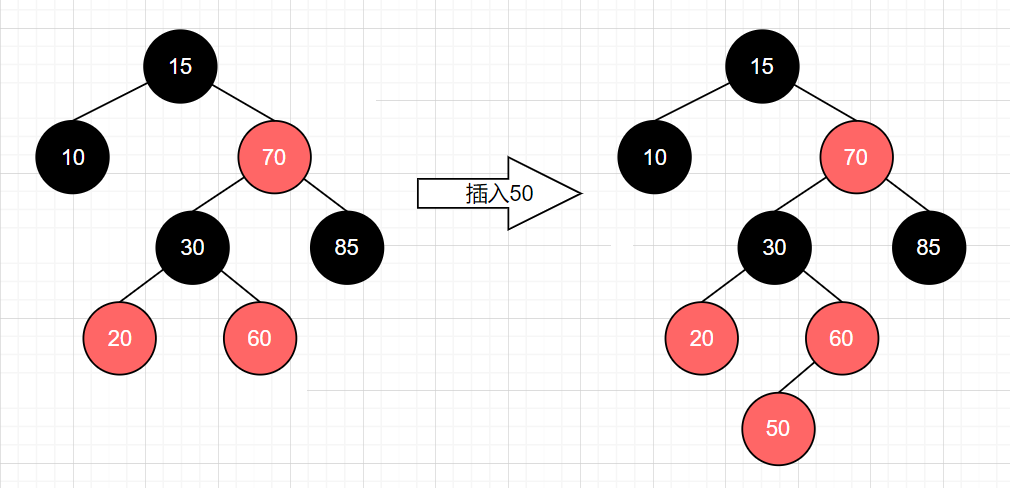
此时结点 50 的父亲结点 60 也为红色，需要进行双红修正。注意到，其叔叔结点 20 也是红色，只需要将父亲结点 60 和叔叔结点 20 变为黑色，再把爷爷结点 30 变为红色，结果如下图。

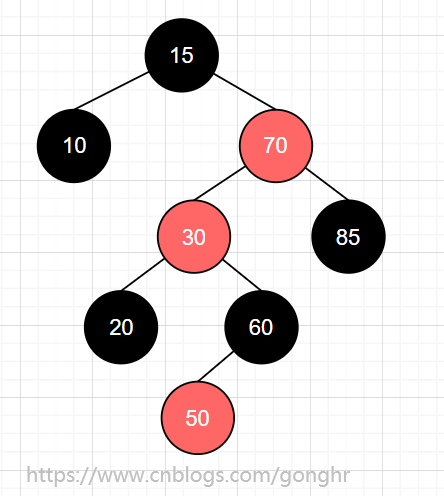
之后会发现，结点 30 和其父结点 70 都为红色，需要进行双红修正。而结点 30 的叔叔结点 85 为黑色，结点 30 的爷爷结点 15 到达结点 30 的路径是 RL 型，故需要先右旋，再左旋。结果如下图。

旋转操作

由于红黑树结点还拥有 parent 属性，故不能像平衡二叉树一样进行旋转（【数据结构与算法】手撕平衡二叉树），需要特殊考虑 parent的赋值。

1️⃣ RR 型

左旋

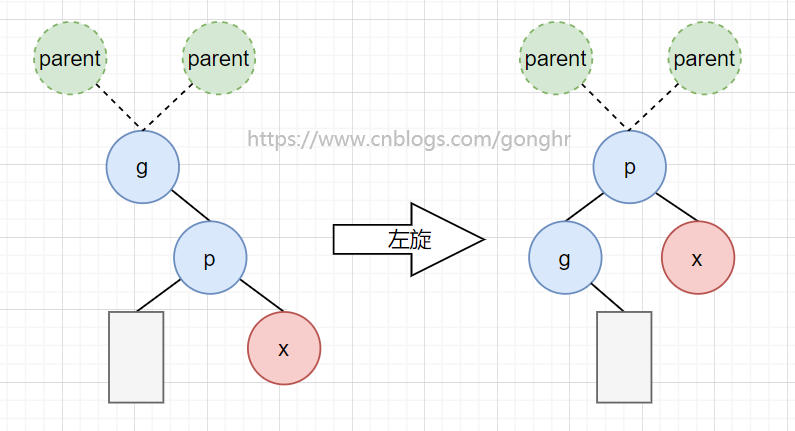
需要特别注意的是爷爷结点 g 的 parent 的设置，需要先判断 g 是左子结点还是右子结点。

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18

java private void leftRotate(RBNode g) { if (g != null) { RBNode p = g.right; g.right = p.left; if (p.left != null) { p.left.parent = g; } p.parent = g.parent; if (g.parent == null) { this.root = p; } else if (g.parent.left == g) { g.parent.left = p; } else { g.parent.right = p; } p.left = g; g.parent = p; }
2️⃣ LL 型

右旋

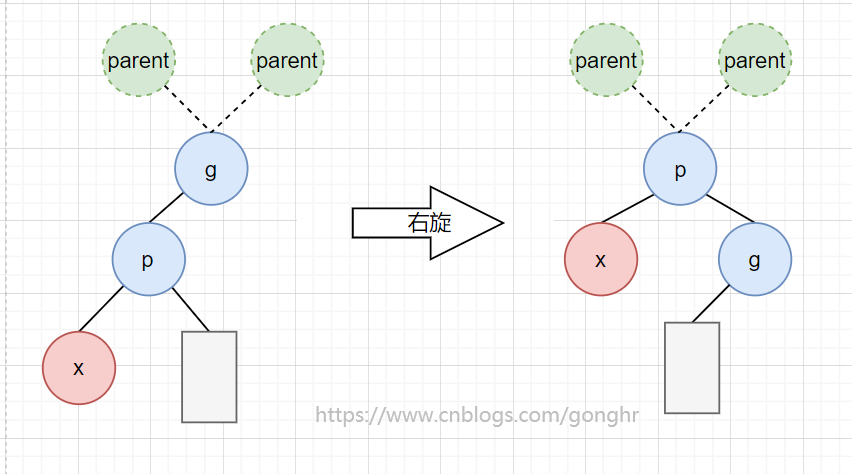
需要特别注意的是爷爷结点 g 的 parent 的设置，需要先判断 g 是左子结点还是右子结点。

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

java private void rightRotate(RBNode g) { if(g != null) { RBNode p = g.left; g.left = p.right; if(p.right != null) { p.right.parent = g; } p.parent = g.parent; if(g.parent == null) { this.root = p; } else if(g.parent.left == g) { g.parent.left = p; } else { g.parent.right = p; } p.right = g; g.parent = p; } }
3️⃣ LR 型

先对 g 的左子结点左旋，再对 g 右旋

复制代码

• 1
• 2
• 3
• 4
• 5
• 6

java private void leftRightRotate(RBNode g) { if(g != null) { leftRotate(g.left); rightRotate(g); } }
4️⃣ RL 型

先对 g 的右子结点右旋，再对 g 左旋

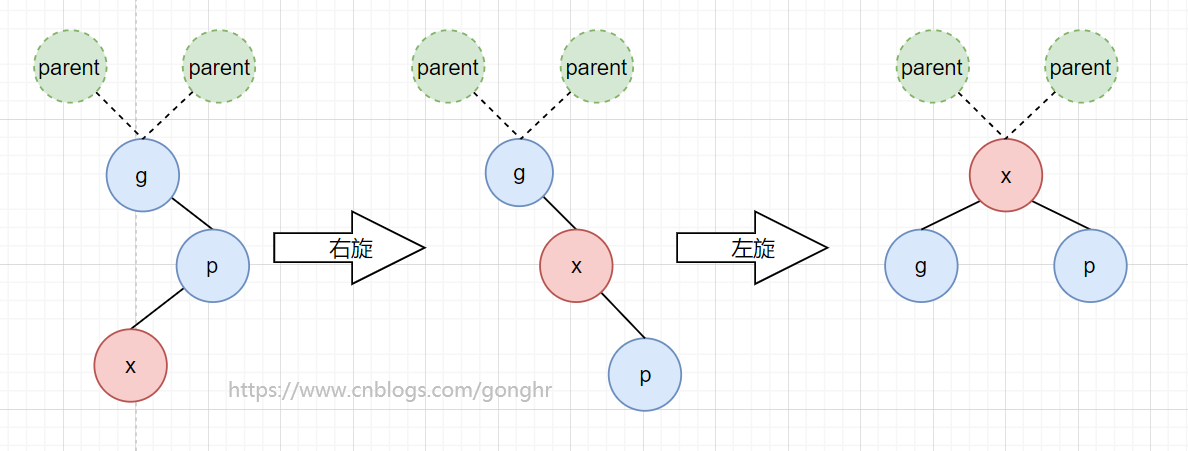
复制代码

• 1
• 2
• 3
• 4
• 5
• 6

java private void rightLeftRotate(RBNode g) { if(g != null) { rightRotate(g.right); leftRotate(g); } }

代码

1️⃣ 插入操作

代码描述

• 如果根结点为空，则创建根结点，返回
• 否则，根据 key 与结点关键值的比较找到插入位置
• 创建结点并插入
• 平衡处理

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30

java public void insert(K key, V value) { RBNode t = this.root; if (t == null) { this.root = new RBNode(null, key, value); setColor(root, BLACK); return; } int cmp = 0; RBNode parent = null; while (t != null) { parent = t; cmp = key.compareTo(t.key); if (cmp 0) { t = t.right; } else { t.value = value; return; } } RBNode e = new RBNode(parent, key, value); if (cmp
2️⃣ 平衡处理

代码描述

• 新插入的结点都设置为红色
• 进入循环，条件是 x 不为空且 x 不为根结点且 x 的父亲为红色（进行双红处理）

• 若父结点是爷爷结点的左子结点，即为 L 类型

  • 令 uncle 为叔叔结点
  • 若叔叔结点为红色：令爷爷结点为红色，父亲结点为黑色，叔叔结点为黑色，x 赋为爷爷结点，进入下一次循环处理。

  • 若叔叔结点为黑色：

    • 若 x 是父结点的右子结点，则为 LR 型，先左旋，再右旋，染色
    • 若 x 是父结点的左子结点，则为 LL 型，左旋，染色

• 若父结点是爷爷结点的右子结点，即为 R 类型

  • 令 uncle 为叔叔结点
  • 若叔叔结点为红色：令爷爷结点为红色，父亲结点为黑色，叔叔结点为黑色，x 赋为爷爷结点，进入下一次循环处理。

  • 若叔叔结点为黑色：

    • 若 x 是父结点的左子结点，则为 RL 型，先右旋，再左旋，染色
    • 若 x 是父结点的右子结点，则为 RR 型，右旋，染色
• 设置根结点为黑色（始终如此）

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43

java private void fixAfterInsert(RBNode x) { setColor(x, RED); while (x != null && x != root && colorOf(x.parent) == RED) { if (x.parent == x.parent.parent.left) { RBNode uncle = x.parent.parent.right; if (colorOf(uncle) == RED) { setColor(x.parent, BLACK); setColor(uncle, BLACK); setColor(x.parent.parent, RED); x = x.parent.parent; } else { if (x == x.parent.right) { leftRightRotate(x.parent.parent); setColor(x, BLACK); setColor(x.right, RED); } else { setColor(x.parent, BLACK); setColor(x.parent.parent, RED); rightRotate(x.parent.parent); } } } else { RBNode uncle = x.parent.parent.left; if (colorOf(uncle) == RED) { setColor(x.parent, BLACK); setColor(uncle, BLACK); setColor(x.parent.parent, RED); x = x.parent.parent; } else { if (x == x.parent.left) { rightLeftRotate(x.parent.parent); setColor(x, BLACK); setColor(x.left, RED); } else { setColor(x.parent, BLACK); setColor(x.parent.parent, RED); leftRotate(x.parent.parent); } } } } setColor(root, BLACK); }

查找前驱和后继结点

1️⃣ 查找前驱结点

• 若当前结点为空，则返回
• 若当前结点存在左子树，则前驱结点是左子树的最右结点
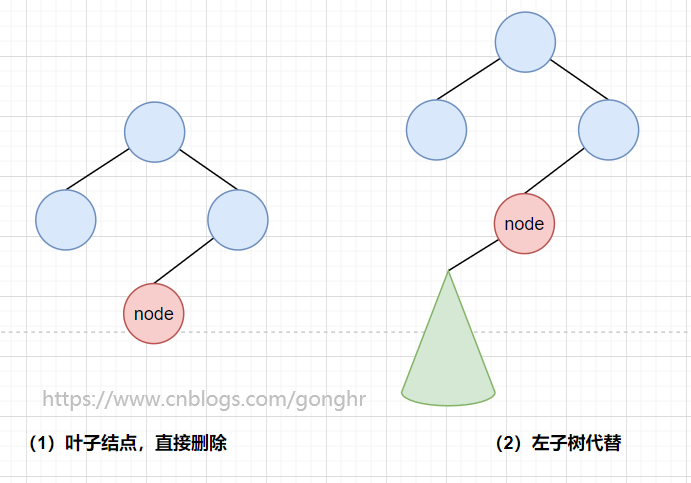
• 若当前结点不存在左子树：注意这种情况在删除时是不用考虑的，要么为叶子结点，可以直接删除；要么可以用右子树代替，不用考虑前驱。这里是求的是严格意义上的前驱结点。
  

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

java private RBNode predecessor(RBNode node) { if (node == null) { return null; } else if (node.left != null) { RBNode p = node.left; while (p.right != null) { p = p.right; } return p; } else { RBNode p = node.parent; RBNode ch = node; while (p != null && ch == p.left) { ch = p; p = p.parent; } return p; } }
2️⃣ 查找后继结点

• 若当前结点为空，则返回
• 若当前结点存在右子树，则前驱结点是右子树的最左结点
• 若当前结点不存在右子树：注意这种情况在删除时是不用考虑的，要么为叶子结点，可以直接删除；要么可以用左子树代替，不用考虑后继。这里是求的是严格意义上的后继结点。
  

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

java private RBNode successor(RBNode node) { if (node == null) { return null; } else if (node.right != null) { RBNode p = node.right; while (p.left != null) { p = p.left; } return p; } else { RBNode p = node.parent; RBNode ch = node; while (p != null && ch == p.right) { ch = p; p = p.parent; } return p; } }

删除算法

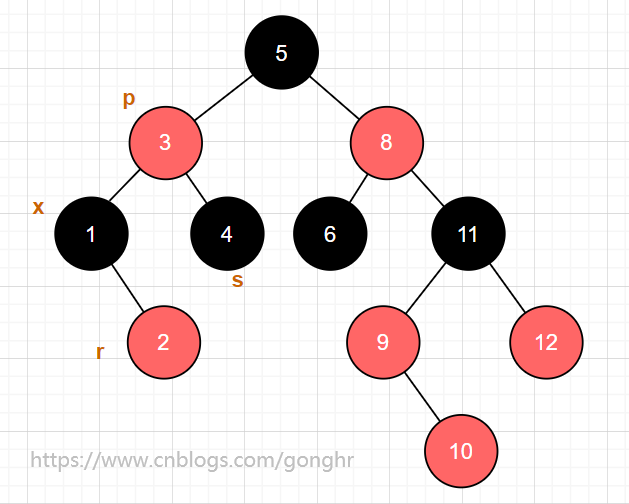
• 定义 x 为实际删除结点，r 为替换 X 的结点，p 为 x 的父亲，s 为 x 的兄弟
• 查找，若查找失败则直接返回，若查找成功则删除对应的结点 x

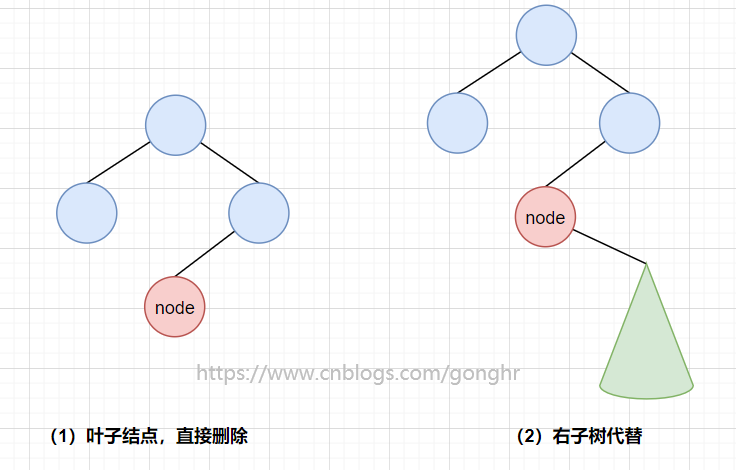
• 删除操作最终可归结为两种情况：删除叶结点和删除只有一个孩子的结点

  • 若 x 为红，则必为红叶子，直接删除
  • 若 x 为黑 r 为红，r 替换 x，并将 r 染黑
  • 若 x 为黑 r 为黑：需要处理双黑缺陷

双黑缺陷

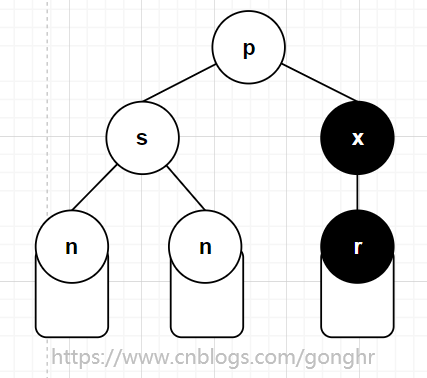
• 若 x 为黑 r 为黑（r 可能为外结点）：双黑缺陷
• x 为实际删除结点，r 为替换 x 的结点，p 为 x 的父亲，s 为 x 的兄弟，n 为 s 的孩子

1️⃣ 兄弟 s 为黑，且有红孩子

• p 到 n 的路径为 LL 型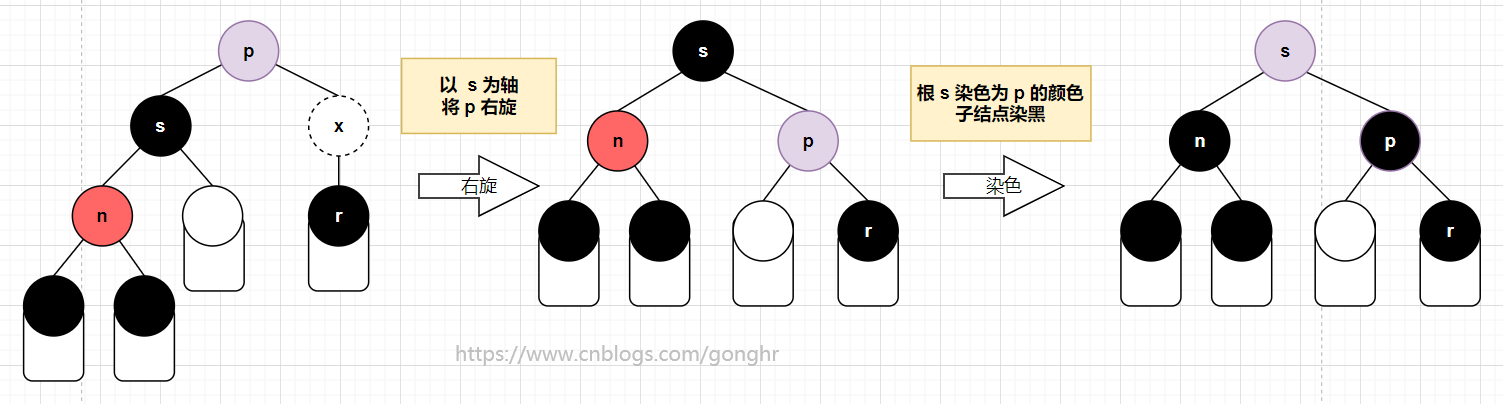
  
• p 到 n 的路径为 LR 型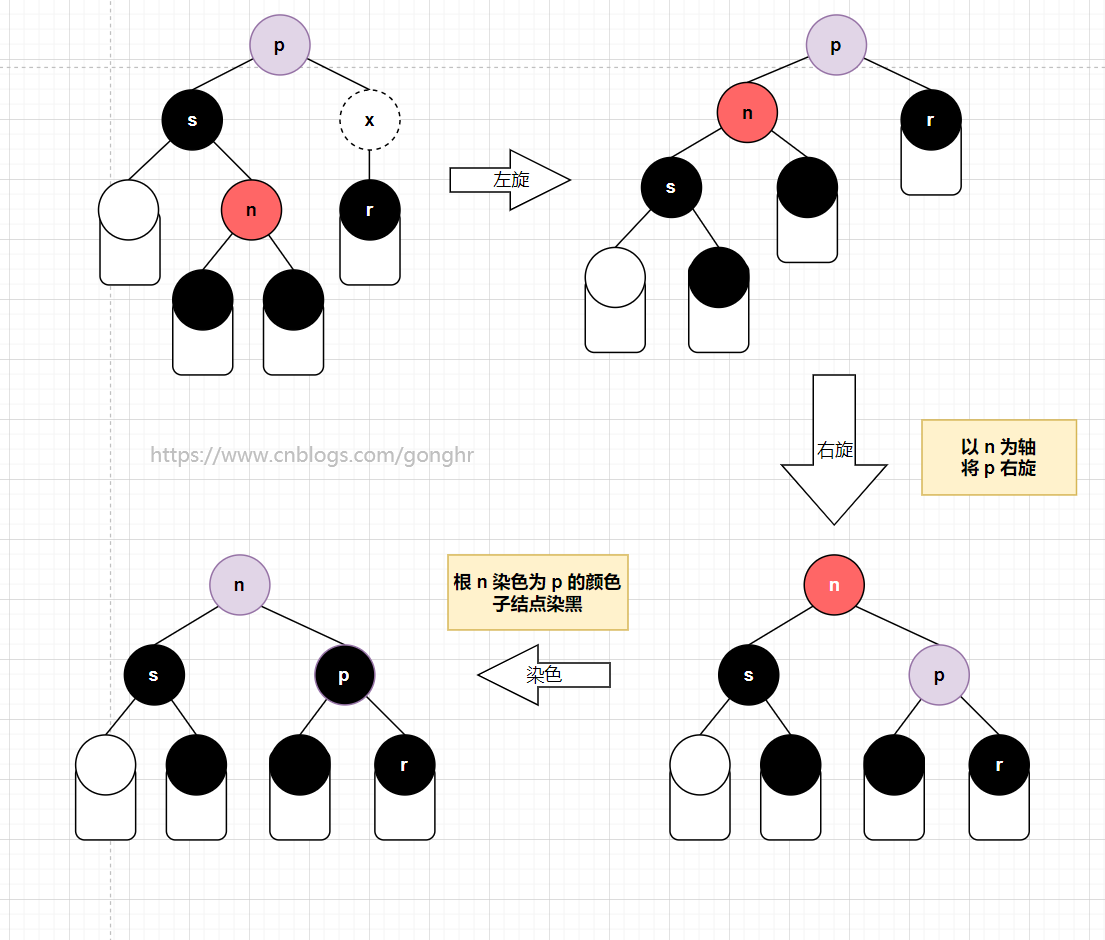
  
• p 到 n 的路径为 RR 型。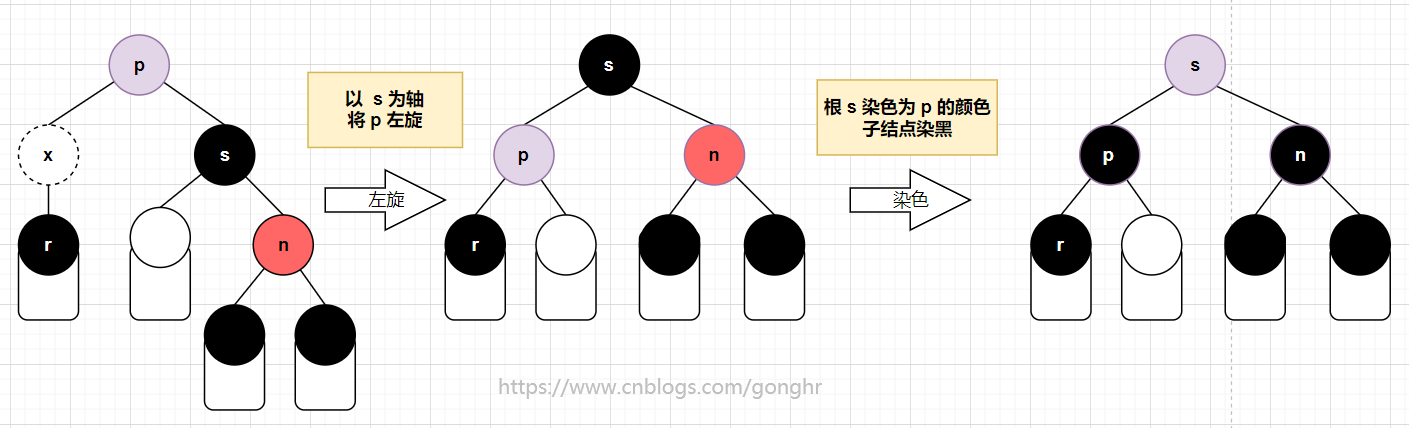
  
• p 到 n 的路径为 RL 型。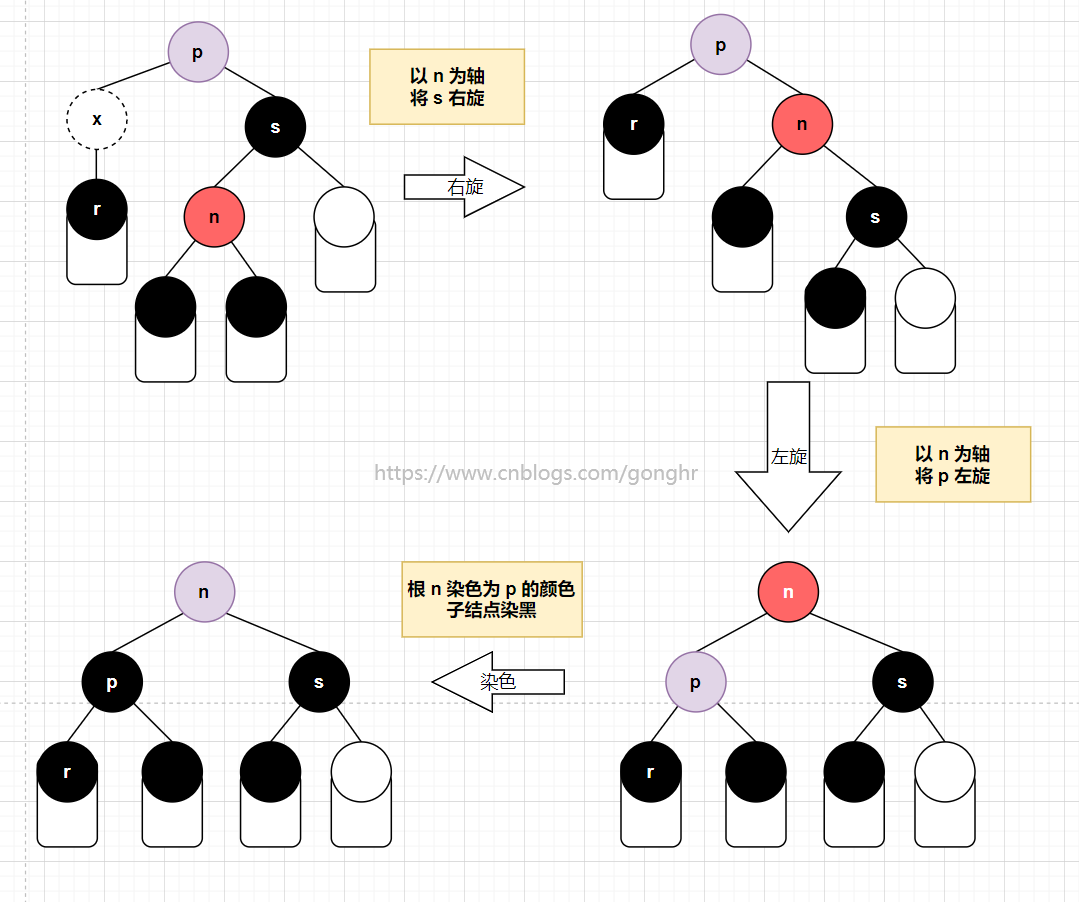
  

2️⃣ 兄弟 s 为黑，无红孩子

• 父亲 p 为红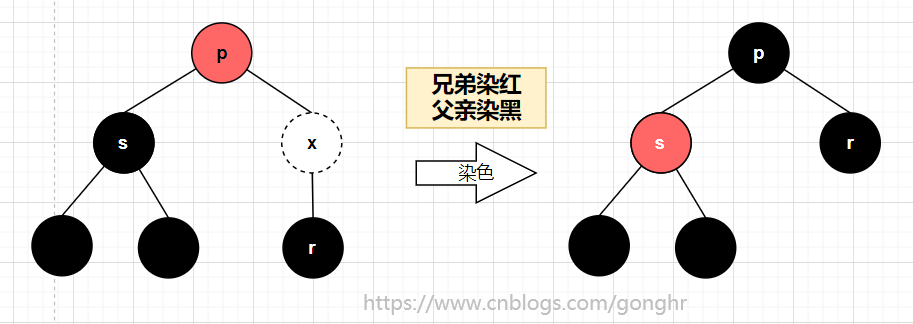
  
• 父亲 p 为黑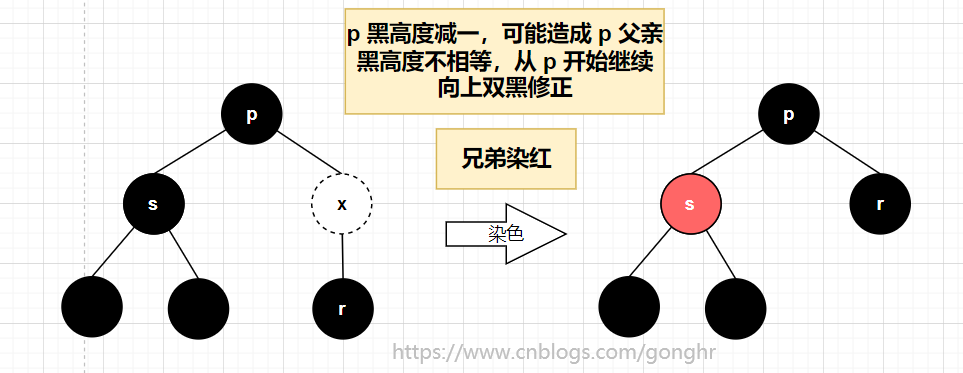
  

3️⃣ 兄弟 s 为红

• s 为 p 的左孩子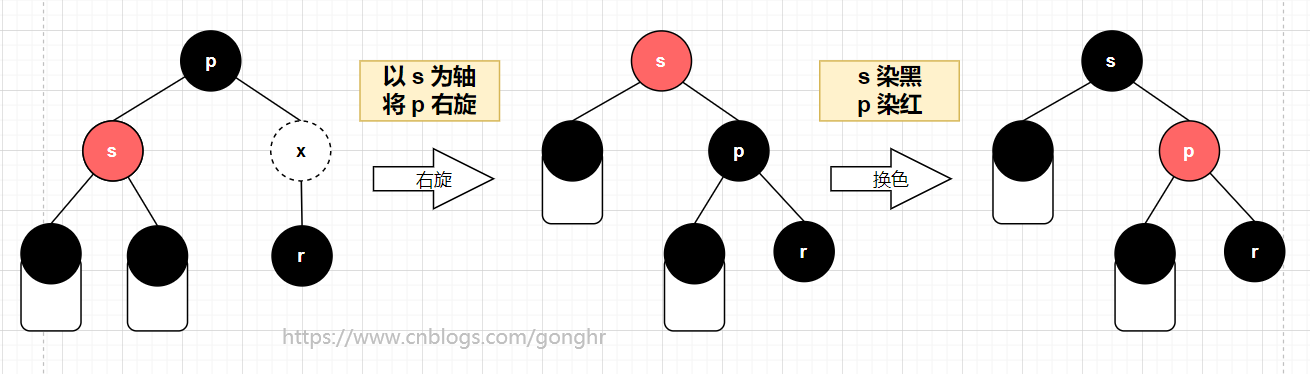
  

经过变换后，问题没有解决，但 r 的兄弟变为黑色，可能转为黑兄弟有红孩子情况（最多需两次旋转），或黑兄弟无红孩子有红父亲情况，需染色。

• s 为 p 的右孩子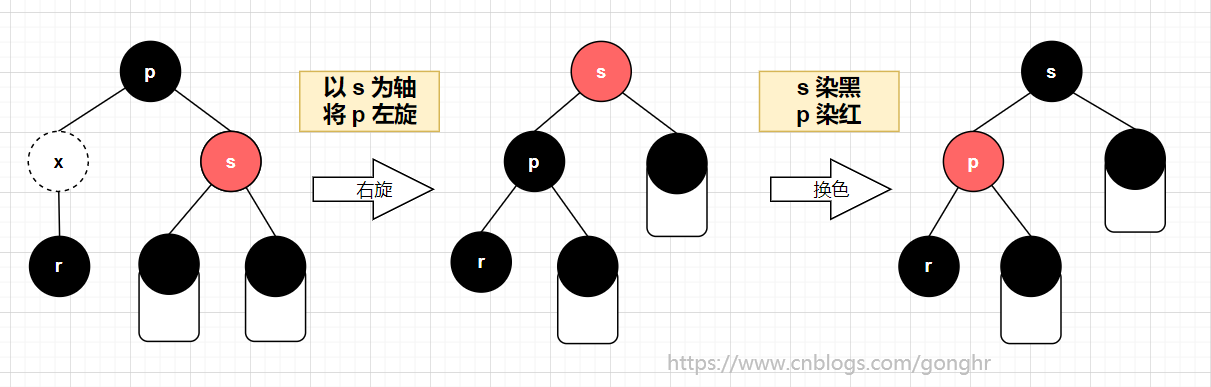
  

经过变换后，问题没有解决，但 r 的兄弟变为黑色，可能转为黑兄弟有红孩子情况（最多需两次旋转），或黑兄弟无红孩子有红父亲情况，需染色。

代码

1️⃣ 删除时先找到要删除的结点

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14

java private RBNode getNode(K key) { RBNode node = this.root; while (node != null) { int cmp = key.compareTo(node.key); if (cmp 0) { node = node.right; } else { return node; } } return null; }
2️⃣ 删除结点

代码描述

• 若要被删除的结点的左右子结点都存在，则找到其中序后继（前驱）结点，将中序结点的值赋给该结点，然后令该结点的引用指向中序结点，用来删除该中序结点
• 令 relpacement 指向结点的非空子结点
• 若 replacemnet 不为空，即找到了该结点的非空子结点，则用该子结点结点替换该结点。特别注意 parent 属性的赋值。若该结点是黑色，处理双黑缺陷。
• 若该结点没有子结点，且父结点为空，说明该结点就是根节点，直接删除

• 若该结点没有子结点，且父结点不是空

  • 若为黑色结点，处理双黑缺陷
  • 删除该结点

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39

java private void deleteNode(RBNode node) { if (node.left != null && node.right != null) { // RBNode predecessor = predecessor(node); // node.value = predecessor.value; // node = predecessor; RBNode successor = successor(node); node.key = successor.key; node.value = successor.value; node = successor; } RBNode replacement = node.left != null ? node.left : node.right; if (replacement != null) { replacement.parent = node.parent; if (node.parent == null) { root = replacement; } else if (node == node.parent.left) { node.parent.left = replacement; } else { node.parent.right = replacement; } node.left = node.right = node.parent = null; if (colorOf(node) == BLACK) { fixAfterRemove(replacement); } } else if (node.parent == null) { root = null; } else { if (colorOf(node) == BLACK) { fixAfterRemove(node); } if (node.parent != null) { if (node == node.parent.left) { node.parent.left = null; } else { node.parent.right = null; } } } }
3️⃣ 处理双黑缺陷

代码描述

• 只要当前结点不是根节点，且颜色为黑色，循环

  • 如果当前结点是左节点，即为 L 型

    • 令 s 为该结点的右兄弟结点
    • 若 s 为红色，说明该结点的兄弟结点为红色，属于情况三（2），将其转化为情况一或二（兄弟结点 s 变为黑）
    • 若 s 为黑色，且无红孩子，属于情况二（将兄弟结点 s 染红），将 x 赋予 x.parent 向上继续双黑修正

    • 否则，若有红孩子

      • 若为 LL 型，右旋 + 染色，属于情况一（1）
      • 若为 LR 型，左右旋 + 染色，属于情况一（2）

  • 如果当前结点是右节点，即为 R 型

    • 令 s 为该结点的左兄弟结点
    • 若 s 为红色，说明该结点的兄弟结点为红色，属于情况三（1），将其转化为情况一或二（兄弟结点 s 变为黑）
    • 若 s 为黑色，且无红孩子，属于情况二（将兄弟结点 s 染红），将 x 赋予 x.parent 向上继续双黑修正

    • 否则，若有红孩子

      • 若为 RR 型，左旋 + 染色，属于情况一（3）
      • 若为 RL 型，右左旋 + 染色，属于情况一（4）
• x 有可能最后指向根结点，必须保证为黑色

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63

java private void fixAfterRemove(RBNode x) { while (x != root && colorOf(x) == BLACK) { if (x == x.parent.left) { RBNode s = x.parent.right; if (colorOf(s) == RED) { leftRotate(x.parent); setColor(s, BLACK); setColor(x.parent, RED); s = x.parent.right; } if (colorOf(s.left) == BLACK && colorOf(s.right) == BLACK) { setColor(s, RED); x = x.parent; } else { if (colorOf(s.right) == BLACK) { RBNode p = s.parent; rightLeftRotate(p); setColor(s, BLACK); setColor(s.parent, p.color); setColor(p, BLACK); x = root; } else { RBNode p = s.parent; leftRotate(p); setColor(s, colorOf(p)); setColor(p, BLACK); setColor(s.right, BLACK); x = root; // 终止循环 } } } else { RBNode s = x.parent.left; if (colorOf(s) == RED) { setColor(s, BLACK); setColor(x.parent, RED); rightRotate(x.parent); s = x.parent.left; } if (colorOf(s.left) == BLACK && colorOf(s.right) == BLACK) { setColor(s, RED); x = x.parent; } else { if (colorOf(s.left) == BLACK) { RBNode p = s.parent; leftRightRotate(p); setColor(s, BLACK); setColor(s.parent, p.color); setColor(p, BLACK); x = root; } else { RBNode p = s.parent; rightRotate(p); setColor(s, colorOf(p)); setColor(p, BLACK); setColor(s.left, BLACK); x = root; } } } } setColor(x, BLACK); }

总结

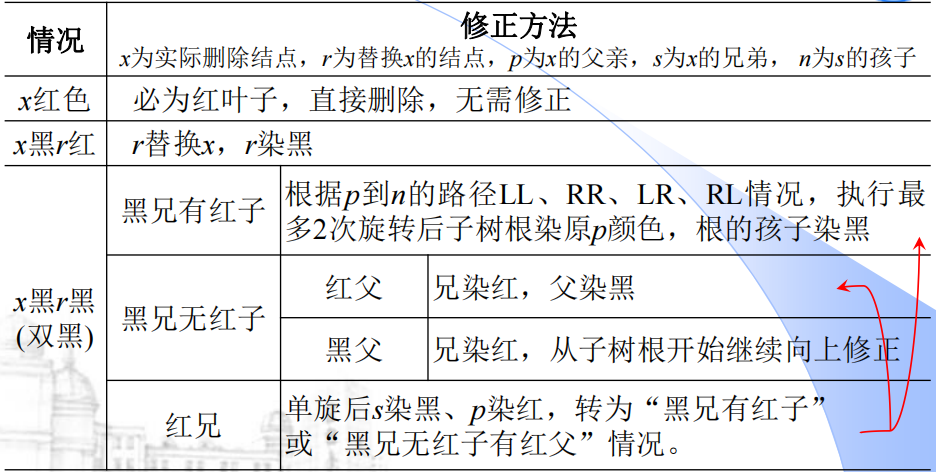
最多涉及 3 次旋转，O(logn) 次染色

AVL 树 vs 红黑树

• 查找、插入、删除最坏时间复杂度均为 O(logn)。
• 红黑树平衡性弱于 AVL 树，故查找性能低于 AVL 树。
• 红黑树插入删除所需的旋转次数较少，插入、删除效率高于 AVL 树。

完整代码

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85
• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98
• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111
• 112
• 113
• 114
• 115
• 116
• 117
• 118
• 119
• 120
• 121
• 122
• 123
• 124
• 125
• 126
• 127
• 128
• 129
• 130
• 131
• 132
• 133
• 134
• 135
• 136
• 137
• 138
• 139
• 140
• 141
• 142
• 143
• 144
• 145
• 146
• 147
• 148
• 149
• 150
• 151
• 152
• 153
• 154
• 155
• 156
• 157
• 158
• 159
• 160
• 161
• 162
• 163
• 164
• 165
• 166
• 167
• 168
• 169
• 170
• 171
• 172
• 173
• 174
• 175
• 176
• 177
• 178
• 179
• 180
• 181
• 182
• 183
• 184
• 185
• 186
• 187
• 188
• 189
• 190
• 191
• 192
• 193
• 194
• 195
• 196
• 197
• 198
• 199
• 200
• 201
• 202
• 203
• 204
• 205
• 206
• 207
• 208
• 209
• 210
• 211
• 212
• 213
• 214
• 215
• 216
• 217
• 218
• 219
• 220
• 221
• 222
• 223
• 224
• 225
• 226
• 227
• 228
• 229
• 230
• 231
• 232
• 233
• 234
• 235
• 236
• 237
• 238
• 239
• 240
• 241
• 242
• 243
• 244
• 245
• 246
• 247
• 248
• 249
• 250
• 251
• 252
• 253
• 254
• 255
• 256
• 257
• 258
• 259
• 260
• 261
• 262
• 263
• 264
• 265
• 266
• 267
• 268
• 269
• 270
• 271
• 272
• 273
• 274
• 275
• 276
• 277
• 278
• 279
• 280
• 281
• 282
• 283
• 284
• 285
• 286
• 287
• 288
• 289
• 290
• 291
• 292
• 293
• 294
• 295
• 296
• 297
• 298
• 299
• 300
• 301
• 302
• 303
• 304
• 305
• 306
• 307
• 308
• 309
• 310
• 311
• 312
• 313
• 314
• 315
• 316
• 317
• 318
• 319
• 320
• 321
• 322
• 323
• 324
• 325
• 326
• 327
• 328
• 329
• 330
• 331
• 332
• 333
• 334
• 335
• 336
• 337
• 338
• 339
• 340
• 341
• 342
• 343
• 344
• 345
• 346

java`class RBTreeextends Comparable, V> {
private static final boolean RED = false;
private static final boolean BLACK = true;
private RBNode root;

private void inorder(RBNode root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " " + (root.color ? "B" : "R") + " ");
inorder(root.right);
}
}

private void preorder(RBNode root) {
if (root != null) {
System.out.print(root.key + " " + (root.color ? "B" : "R") + " ");
preorder(root.left);
preorder(root.right);
}
}

public void preorderTraverse() {
preorder(this.root);
System.out.println();
}

public void inorderTraverse() {
inorder(this.root);
System.out.println();
}

public boolean colorOf(RBNode node) {
return node != null ? node.color : BLACK;
}

public void insert(K key, V value) {
RBNode t = this.root;
if (t == null) {
this.root = new RBNode(null, key, value);
setColor(root, BLACK);
return;
}
int cmp = 0;
RBNode parent = null;
while (t != null) {
parent = t;
cmp = key.compareTo(t.key);
if (cmp < 0) {
t = t.left;
} else if (cmp > 0) {
t = t.right;
} else {
t.value = value;
return;
}
}
RBNode e = new RBNode(parent, key, value);
if (cmp < 0) {
parent.left = e;
} else {
parent.right = e;
}
// 平衡处理，旋转+变色
fixAfterInsert(e);
}

private void fixAfterInsert(RBNode x) {
setColor(x, RED);
while (x != null && x != root && colorOf(x.parent) == RED) {
if (x.parent == x.parent.parent.left) {
RBNode uncle = x.parent.parent.right;
if (colorOf(uncle) == RED) {
setColor(x.parent, BLACK);
setColor(uncle, BLACK);
setColor(x.parent.parent, RED);
x = x.parent.parent;
} else {
if (x == x.parent.right) {
leftRightRotate(x.parent.parent);
setColor(x, BLACK);
setColor(x.right, RED);
} else {
setColor(x.parent, BLACK);
setColor(x.parent.parent, RED);
rightRotate(x.parent.parent);
}
}
} else {
RBNode uncle = x.parent.parent.left;
if (colorOf(uncle) == RED) {
setColor(x.parent, BLACK);
setColor(uncle, BLACK);
setColor(x.parent.parent, RED);
x = x.parent.parent;
} else {
if (x == x.parent.left) {
rightLeftRotate(x.parent.parent);
setColor(x, BLACK);
setColor(x.left, RED);
} else {
setColor(x.parent, BLACK);
setColor(x.parent.parent, RED);
leftRotate(x.parent.parent);
}
}
}
}
setColor(root, BLACK);
}

private RBNode predecessor(RBNode node) {
if (node == null) {
return null;
} else if (node.left != null) {
RBNode p = node.left;
while (p.right != null) {
p = p.right;
}
return p;
} else {
RBNode p = node.parent;
RBNode ch = node;
while (p != null && ch == p.left) {
ch = p;
p = p.parent;
}
return p;
}
}

private RBNode successor(RBNode node) {
if (node == null) {
return null;
} else if (node.right != null) {
RBNode p = node.right;
while (p.left != null) {
p = p.left;
}
return p;
} else {
RBNode p = node.parent;
RBNode ch = node;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}

public void remove(K key) {
RBNode node = getNode(key);
if (node == null) return;
deleteNode(node);
return;
}

private void deleteNode(RBNode node) {
if (node.left != null && node.right != null) {
// RBNode predecessor = predecessor(node);
// node.value = predecessor.value;
// node = predecessor;
RBNode successor = successor(node);
node.key = successor.key;
node.value = successor.value;
node = successor;
}
RBNode replacement = node.left != null ? node.left : node.right;
if (replacement != null) {
replacement.parent = node.parent;
if (node.parent == null) {
root = replacement;
} else if (node == node.parent.left) {
node.parent.left = replacement;
} else {
node.parent.right = replacement;
}
node.left = node.right = node.parent = null;
if (colorOf(node) == BLACK) {
fixAfterRemove(replacement);
}
} else if (node.parent == null) {
root = null;
} else {
if (colorOf(node) == BLACK) {
fixAfterRemove(node);
}
if (node.parent != null) {
if (node == node.parent.left) {
node.parent.left = null;
} else {
node.parent.right = null;
}
}
}
}

private void fixAfterRemove(RBNode x) {
while (x != root && colorOf(x) == BLACK) {
if (x == x.parent.left) {
RBNode s = x.parent.right;
if (colorOf(s) == RED) {
leftRotate(x.parent);
setColor(s, BLACK);
setColor(x.parent, RED);
s = x.parent.right;
}
if (colorOf(s.left) == BLACK && colorOf(s.right) == BLACK) {
setColor(s, RED);
x = x.parent;
} else {
if (colorOf(s.right) == BLACK) {
RBNode p = s.parent;
rightLeftRotate(p);
setColor(s, BLACK);
setColor(s.parent, p.color);
setColor(p, BLACK);
x = root;
} else {
RBNode p = s.parent;
leftRotate(p);
setColor(s, colorOf(p));
setColor(p, BLACK);
setColor(s.right, BLACK);
x = root; // 终止循环
}
}
} else {
RBNode s = x.parent.left;
if (colorOf(s) == RED) {
setColor(s, BLACK);
setColor(x.parent, RED);
rightRotate(x.parent);
s = x.parent.left;
}
if (colorOf(s.left) == BLACK && colorOf(s.right) == BLACK) {
setColor(s, RED);
x = x.parent;
} else {
if (colorOf(s.left) == BLACK) {
RBNode p = s.parent;
leftRightRotate(p);
setColor(s, BLACK);
setColor(s.parent, p.color);
setColor(p, BLACK);
x = root;
} else {
RBNode p = s.parent;
rightRotate(p);
setColor(s, colorOf(p));
setColor(p, BLACK);
setColor(s.left, BLACK);
x = root;
}
}
}
}
setColor(x, BLACK);
}

private RBNode getNode(K key) {
RBNode node = this.root;
while (node != null) {
int cmp = key.compareTo(node.key);
if (cmp < 0) {
node = node.left;
} else if (cmp > 0) {
node = node.right;
} else {
return node;
}
}
return null;
}

private void setColor(RBNode node, boolean color) {
if (node != null) {
node.color = color;
}
}

private void leftRotate(RBNode g) {
if (g != null) {
RBNode p = g.right;
g.right = p.left;
if (p.left != null) {
p.left.parent = g;
}
p.parent = g.parent;
if (g.parent == null) {
this.root = p;
} else if (g.parent.left == g) {
g.parent.left = p;
} else {
g.parent.right = p;
}
p.left = g;
g.parent = p;
}
}

private void rightRotate(RBNode g) {
if (g != null) {
RBNode p = g.left;
g.left = p.right;
if (p.right != null) {
p.right.parent = g;
}
p.parent = g.parent;
if (g.parent == null) {
this.root = p;
} else if (g.parent.left == g) {
g.parent.left = p;
} else {
g.parent.right = p;
}
p.right = g;
g.parent = p;
}
}

private void leftRightRotate(RBNode g) {
leftRotate(g.left);
rightRotate(g);
}

private void rightLeftRotate(RBNode g) {
rightRotate(g.right);
leftRotate(g);
}
}

class RBNodeextends Comparable, V> {
public RBNode parent;
public RBNode left;
public RBNode right;
public boolean color;
public K key;
public V value;

public RBNode(RBNode parent, K key, V value) {
this.parent = parent;
this.key = key;
this.value = value;
}
}`
? 方法测试

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18

java public static void main(String[] args) { RBTree tree = new RBTree(); Scanner scanner = new Scanner(System.in); int n; n = scanner.nextInt(); while (n-- > 0) { String operation = scanner.next(); String value = scanner.next(); if (operation.equals("Insert")) { tree.insert(Integer.parseInt(value), 1); } else { tree.remove(Integer.parseInt(value)); } } tree.inorderTraverse(); System.out.println(); tree.preorderTraverse(); }
输入：

复制代码

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33

text32 Insert 10 Insert 40 Insert 30 Insert 60 Insert 90 Insert 70 Insert 20 Insert 50 Insert 80 Insert 10 Insert 66 Insert 85 Insert 60 Insert 12 Insert 32 Insert 74 Insert 7 Insert 52 Insert -5 Insert 13 Insert 23 Insert 13 Insert 103 Insert 306 Insert 2 Insert -97 Insert 752 Remove 90 Remove 60 Remove 70 Remove 50 Remove 80
输出：

复制代码

• 1
• 2
• 3

text`-97 R -5 B 2 R 7 R 10 B 12 B 13 R 20 B 23 R 30 R 32 B 40 B 52 B 66 B 74 B 85 B 103 B 306 R 752 B

66 B 30 R 12 B 7 R -5 B -97 R 2 R 10 B 20 B 13 R 23 R 40 B 32 B 52 B 85 B 74 B 306 R 103 B 752 B`

转载请注明：xuhss » 【数据结构与算法】手撕红黑树