Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475
最近在做眼底图像的无监督分类，使用的数据集辣子kaggle的Diabetic Retinopathy，简称DR，中文称糖尿病型眼底疾病。

最后的评估方法是二次加权kappa。以前没接触过，网上也没有具体的介绍，在这里简单谈谈我的理解，如有错误欢迎指出。

简介

Kappa指数用来衡量两个模型对同一张图片进行判断时，判断结果一致的程度，结果范围从0~1，1表示评价完全相同，0表示评价完全相反。

一般用模型获得相同评价的数量与基于可能性的期望是否有差别来分析，当两个模型相同评价的数量和基于可能性期望的数量基本一样时，kappa的值就接近于1。

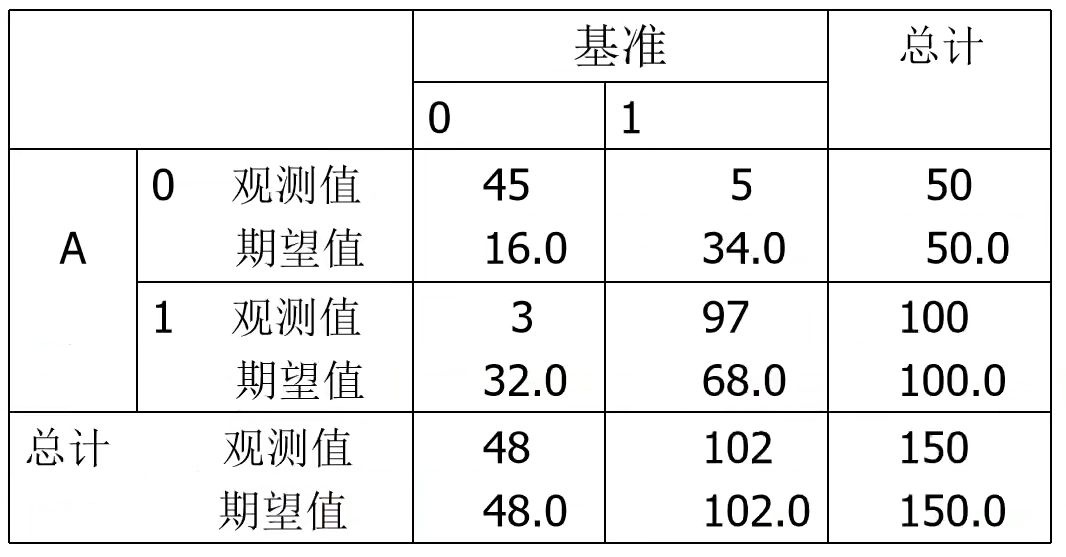
举个栗子，模型A和基准的kappa：

kappa = (p0-pe) / (n-pe)

其中，P0 = 对角线单元中观测值的总和；pe = 对角线单元中期望值的总和。

根据kappa的计算方法分为简单kappa（simple kappa）和加权kappa（weighted kappa），加权kappa又分为linear weighted kappa和quadratic weighted kappa。

weighted kappa

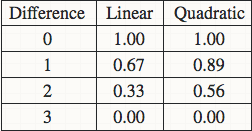
关于linear还是quadratic weighted kappa的选择，取决于你的数据集中不同class之间差异的意义。比如对于眼底图像识别的数据，class=0为健康，class=4为疾病晚期非常严重，所以对于把class=0预测成4的行为所造成的惩罚应该远远大于把class=0预测成class=1的行为，使用quadratic的话0->4所造成的惩罚就等于16倍的0->1的惩罚。如下图是一个四分类的两个计算方法的比较。

Python实现

参考：https://github.com/benhamner/Metrics/blob/master/Python/ml_metrics/quadratic_weighted_kappa.py

#! /usr/bin/env python2.7

import numpy as np

def confusion\_matrix(rater\_a, rater\_b, min\_rating=None, max\_rating=None):
    """
 Returns the confusion matrix between rater's ratings
 """
    assert(len(rater_a) == len(rater_b))
    if min_rating is None:
        min_rating = min(rater_a + rater_b)
    if max_rating is None:
        max_rating = max(rater_a + rater_b)
    num_ratings = int(max_rating - min_rating + 1)
    conf_mat = [[0 for i in range(num_ratings)]
                for j in range(num_ratings)]
    for a, b in zip(rater_a, rater_b):
        conf_mat[a - min_rating][b - min_rating] += 1
    return conf_mat

def histogram(ratings, min\_rating=None, max\_rating=None):
    """
 Returns the counts of each type of rating that a rater made
 """
    if min_rating is None:
        min_rating = min(ratings)
    if max_rating is None:
        max_rating = max(ratings)
    num_ratings = int(max_rating - min_rating + 1)
    hist_ratings = [0 for x in range(num_ratings)]
    for r in ratings:
        hist_ratings[r - min_rating] += 1
    return hist_ratings

def quadratic\_weighted\_kappa(rater\_a, rater\_b, min\_rating=None, max\_rating=None):
    """
 Calculates the quadratic weighted kappa
 quadratic\_weighted\_kappa calculates the quadratic weighted kappa
 value, which is a measure of inter-rater agreement between two raters
 that provide discrete numeric ratings. Potential values range from -1
 (representing complete disagreement) to 1 (representing complete
 agreement). A kappa value of 0 is expected if all agreement is due to
 chance.

 quadratic\_weighted\_kappa(rater\_a, rater\_b), where rater\_a and rater\_b
 each correspond to a list of integer ratings. These lists must have the
 same length.

 The ratings should be integers, and it is assumed that they contain
 the complete range of possible ratings.

 quadratic\_weighted\_kappa(X, min\_rating, max\_rating), where min\_rating
 is the minimum possible rating, and max\_rating is the maximum possible
 rating
 """
    rater_a = np.array(rater_a, dtype=int)
    rater_b = np.array(rater_b, dtype=int)
    assert(len(rater_a) == len(rater_b))
    if min_rating is None:
        min_rating = min(min(rater_a), min(rater_b))
    if max_rating is None:
        max_rating = max(max(rater_a), max(rater_b))
    conf_mat = confusion_matrix(rater_a, rater_b,
                                min_rating, max_rating)
    num_ratings = len(conf_mat)
    num_scored_items = float(len(rater_a))

    hist_rater_a = histogram(rater_a, min_rating, max_rating)
    hist_rater_b = histogram(rater_b, min_rating, max_rating)

    numerator = 0.0
    denominator = 0.0

    for i in range(num_ratings):
        for j in range(num_ratings):
            expected_count = (hist_rater_a[i] * hist_rater_b[j]
                              / num_scored_items)
            d = pow(i - j, 2.0) / pow(num_ratings - 1, 2.0)
            numerator += d * conf_mat[i][j] / num_scored_items
            denominator += d * expected_count / num_scored_items

    return 1.0 - numerator / denominator

def linear\_weighted\_kappa(rater\_a, rater\_b, min\_rating=None, max\_rating=None):
    """
 Calculates the linear weighted kappa
 linear\_weighted\_kappa calculates the linear weighted kappa
 value, which is a measure of inter-rater agreement between two raters
 that provide discrete numeric ratings. Potential values range from -1
 (representing complete disagreement) to 1 (representing complete
 agreement). A kappa value of 0 is expected if all agreement is due to
 chance.

 linear\_weighted\_kappa(rater\_a, rater\_b), where rater\_a and rater\_b
 each correspond to a list of integer ratings. These lists must have the
 same length.

 The ratings should be integers, and it is assumed that they contain
 the complete range of possible ratings.

 linear\_weighted\_kappa(X, min\_rating, max\_rating), where min\_rating
 is the minimum possible rating, and max\_rating is the maximum possible
 rating
 """
    assert(len(rater_a) == len(rater_b))
    if min_rating is None:
        min_rating = min(rater_a + rater_b)
    if max_rating is None:
        max_rating = max(rater_a + rater_b)
    conf_mat = confusion_matrix(rater_a, rater_b,
                                min_rating, max_rating)
    num_ratings = len(conf_mat)
    num_scored_items = float(len(rater_a))

    hist_rater_a = histogram(rater_a, min_rating, max_rating)
    hist_rater_b = histogram(rater_b, min_rating, max_rating)

    numerator = 0.0
    denominator = 0.0

    for i in range(num_ratings):
        for j in range(num_ratings):
            expected_count = (hist_rater_a[i] * hist_rater_b[j]
                              / num_scored_items)
            d = abs(i - j) / float(num_ratings - 1)
            numerator += d * conf_mat[i][j] / num_scored_items
            denominator += d * expected_count / num_scored_items

    return 1.0 - numerator / denominator

def kappa(rater\_a, rater\_b, min\_rating=None, max\_rating=None):
    """
 Calculates the kappa
 kappa calculates the kappa
 value, which is a measure of inter-rater agreement between two raters
 that provide discrete numeric ratings. Potential values range from -1
 (representing complete disagreement) to 1 (representing complete
 agreement). A kappa value of 0 is expected if all agreement is due to
 chance.

 kappa(rater\_a, rater\_b), where rater\_a and rater\_b
 each correspond to a list of integer ratings. These lists must have the
 same length.

 The ratings should be integers, and it is assumed that they contain
 the complete range of possible ratings.

 kappa(X, min\_rating, max\_rating), where min\_rating
 is the minimum possible rating, and max\_rating is the maximum possible
 rating
 """
    assert(len(rater_a) == len(rater_b))
    if min_rating is None:
        min_rating = min(rater_a + rater_b)
    if max_rating is None:
        max_rating = max(rater_a + rater_b)
    conf_mat = confusion_matrix(rater_a, rater_b,
                                min_rating, max_rating)
    num_ratings = len(conf_mat)
    num_scored_items = float(len(rater_a))

    hist_rater_a = histogram(rater_a, min_rating, max_rating)
    hist_rater_b = histogram(rater_b, min_rating, max_rating)

    numerator = 0.0
    denominator = 0.0

    for i in range(num_ratings):
        for j in range(num_ratings):
            expected_count = (hist_rater_a[i] * hist_rater_b[j]
                              / num_scored_items)
            if i == j:
                d = 0.0
            else:
                d = 1.0
            numerator += d * conf_mat[i][j] / num_scored_items
            denominator += d * expected_count / num_scored_items

    return 1.0 - numerator / denominator

def mean\_quadratic\_weighted\_kappa(kappas, weights=None):
    """
 Calculates the mean of the quadratic
 weighted kappas after applying Fisher's r-to-z transform, which is
 approximately a variance-stabilizing transformation. This
 transformation is undefined if one of the kappas is 1.0, so all kappa
 values are capped in the range (-0.999, 0.999). The reverse
 transformation is then applied before returning the result.

 mean\_quadratic\_weighted\_kappa(kappas), where kappas is a vector of
 kappa values

 mean\_quadratic\_weighted\_kappa(kappas, weights), where weights is a vector
 of weights that is the same size as kappas. Weights are applied in the
 z-space
 """
    kappas = np.array(kappas, dtype=float)
    if weights is None:
        weights = np.ones(np.shape(kappas))
    else:
        weights = weights / np.mean(weights)

    # ensure that kappas are in the range [-.999, .999]
    kappas = np.array([min(x, .999) for x in kappas])
    kappas = np.array([max(x, -.999) for x in kappas])

    z = 0.5 * np.log((1 + kappas) / (1 - kappas)) * weights
    z = np.mean(z)
    return (np.exp(2 * z) - 1) / (np.exp(2 * z) + 1)

def weighted\_mean\_quadratic\_weighted\_kappa(solution, submission):
    predicted_score = submission[submission.columns[-1]].copy()
    predicted_score.name = "predicted\_score"
    if predicted_score.index[0] == 0:
        predicted_score = predicted_score[:len(solution)]
        predicted_score.index = solution.index
    combined = solution.join(predicted_score, how="left")
    groups = combined.groupby(by="essay\_set")
    kappas = [quadratic_weighted_kappa(group[1]["essay\_score"], group[1]["predicted\_score"]) for group in groups]
    weights = [group[1]["essay\_weight"].irow(0) for group in groups]
    return mean_quadratic_weighted_kappa(kappas, weights=weights)

转载请注明：xuhss » 一致性检验评价方法kappa