Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475

1树的定义及相关术语

1.1 树的定义

• 树是一种非线性的数据结构，由n(n>=0)个结点组成的有限集合；
  • 如果n=0，称为空树；
  • 如果n>0，则：
    • 有一个特定的结点被称之为根结点(root)，根结点只有直接后继，没有前驱；
    • 除根结点外的其他结点划分为m(m>=0)个互不相交的有限集合T0,T1...Tm-1，每一个集合又是一颗子树，并称之为根的子树。

1.2 树的特点

• 每个结点有零个或多个子结点；
• 没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树；
• 节点的数量等于边数加一；树由n 个节点 和 (n-1)条边 构成，其中n ≥ 1；
• 树或栈这种数据结构用于解决 具有完全包含关系的问题；
• 问题抽象（思维逻辑）：本质上是把一个大问题分成若干个小问题，当小问题解决了，大问题自然也解决了；首先，将树中的“节点”看作“集合”，“边”看作“关系”，接着把“全集”看成是一个大问题，而“子集”看作是若干个小问题，我们只需要关注小问题的求解即可。

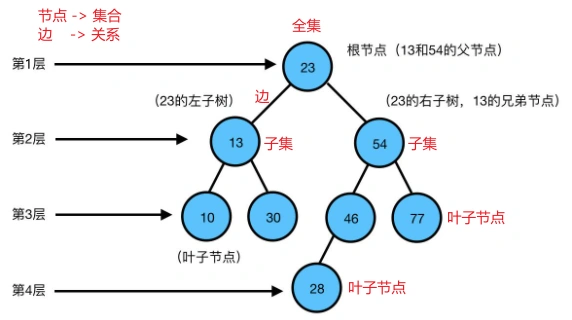
1.3 树的相关术语

• 节点深度：对任意节点x，x节点的深度表示为根节点到x节点的路径长度。所以根节点深度为0，第二层节点深度为1，以此类推；
• 节点高度：对任意节点x，叶子节点到x节点的路径长度就是节点x的高度；
• 树的深度（高度）：一棵树中节点的最大深度就是树的深度，也称为树的高度；
• 度：节点的子树数目就是节点的度；
• 叶子节点 vs 分支节点：度为零的节点就是叶子节点（路径中的最后一个节点）；度不为零的节点就是分支节点；
• 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：拥有共同父节点的节点互称为兄弟节点；
• 节点的层次：从根节点开始，根节点为第一层，根的子节点为第二层，以此类推；
• 祖先：对任意节点x，从根节点到节点x的所有节点都是x的祖先（节点x也是自己的祖先）
• 后代：对任意节点x，从节点x到叶子节点的所有节点都是x的后代（节点x也是自己的后代）
• 森林：m颗互不相交的树构成的集合就是森林
• n叉树：由一个节点向外最多引出节点的数量，即当前这个节点最多向外有n个指向；
• 补充：度分为“入度”和“出度”；
  • 出度：由一个节点向外指向边的数量；
  • 入度：有多少条边指向一个节点的数量；树的入度为1，所以只考虑出度，即为度；
• 案例：
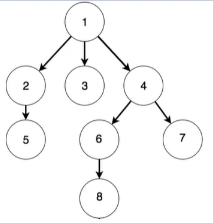
  • 树的深度（高度）：4，path = 1→4→6→8
  • 节点4的深度：2，path = 1→4；节点4的高度：3，path = 8→6→4
  • 节点2的度：1, =(5, )；节点4的度：2，=(6, 7)；叶子节点的度：0

2 二叉树

2.1 定义

• 在一个树中，由一个节点向外最多引出2个节点，即当前这个节点最多向外有2个指向；

2.2 n叉树 vs 二叉树

如何定义n叉树，n是多少的问题？

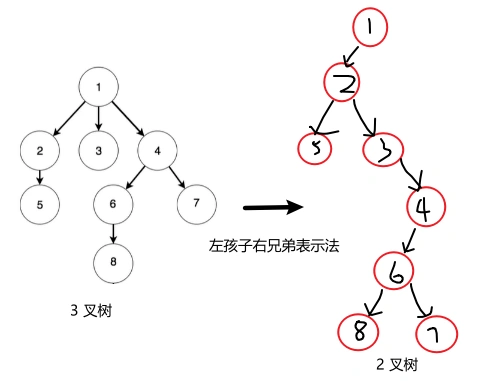
• 对于n叉树中的n是一个不确定性的问题，一般计算机只能处理确定性问题，所以，我们可以将n 叉树转换为2叉树来思考；
• 由于计算机底层是基于二进制计算的，故2 叉树 与 n叉树之间可以相互转换；
• 表示方法：左孩子右兄弟表示法，又名十字链表法

2.3 特点

• 每个节点的度最多为2；
• 度为0的节点比度为2的节点多1个；
  • 证明：参考公式 —> 节点的数量等于边数加一
  • xi：表示度为i的节点数，其中i 为 0，1，2。总共的节点数 = x2 + x1 + x0，度为2提供的边数：2x2， 度为1提供的边数：x1，度为0提供的边数：0；所以 节点数 = 边数 + 1==> x2 + x1 + x0 = 2x2 + x1 + 1 ==> x0 = x2 + 1

2.4 遍历

• 二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点仅被访问一次。
• 二叉树的访问次序：前序遍历、中序遍历、后序遍历

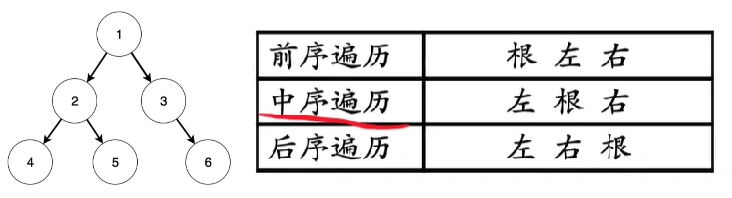
• 前序遍历：1→2→4→5→3→6
• 中序遍历：4→2→5→1→3→6
• 后序遍历：4→5→2→6→3→1

2.5 分类

• 中国版

• 国际版

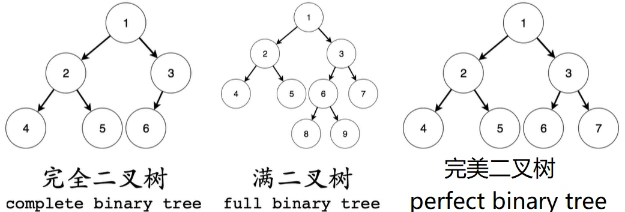
• 完美二叉树：叶子节点都在同一层并且除叶子节点外的所有节点都有两个子节点；
• 完全二叉树（重点）：对于一颗二叉树，假设其深度为d（d>1）。除第d层外的所有节点构成完美二叉树，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；
• 完全二叉树的优势：从根节点到叶子节点中的每一个节点进行一个顺序（连续）标号；
• 完全二叉树的特点：
  • 编号为i的子节点：左孩子编号为2i，右孩子编号为2i+1，注：i ≥ 1;
  • 若 i 从0 开始标记，则左孩子编号为2i + 1，右孩子编号为2i+2，无意中多了一次加法运算；（不建议）
  • 可以用连续空间存储（数组）；
• 完全二叉树实现方式：顺序表 和 链表

2.6 广义表

可以使用广义表来表示一颗二叉树

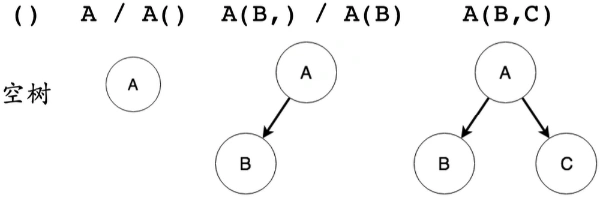
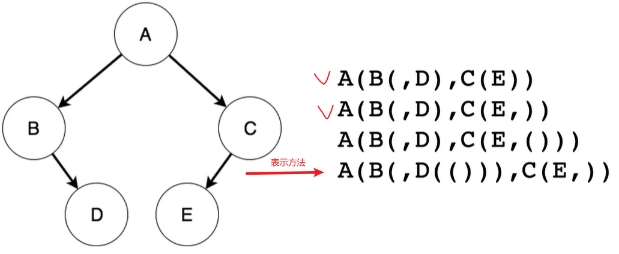
2.7 二叉排序树

• 本质：基于二叉树这种结构，定义了一种性质，并且在不断维护这种性质的一种新结构。
• 性质：一颗二叉树中的任何三元组都满足 B(左孩子) < A(根节点) < C (右孩子)的这种关系。故中序遍历即可实现排序操作。
• 补充：数据结构的本质：定义一种性质，并且维护这种性质的一种结构

2.8 广义表转二叉树

• 通过“栈”这种数据结构实现广义表转二叉树；

3 代码展示

3.1 二叉排序树

#include 
#include 
#include 

typedef struct Node {
    int data;
    struct Node *lchild, *rchild;
} Node;

typedef struct Tree {
    Node *root;
    int length; // 记录二叉树的节点个数
} Tree;

Node *getNewNode(int val);
Tree *getNewTree();
Node *insert\_node(Node *, int, int *);
void insert(Tree *, int);
void pre\_order\_node(Node *);
void pre\_order(Tree *);
void in\_order\_node(Node *);
void in\_order(Tree *);
void post\_order\_node(Node *);
void post\_order(Tree *);
void clear\_node(Node *);
void clear(Tree *);
void output\_node(Node *);
void output(Tree *);

int main() {
    srand(time(0));
    Tree *tree = getNewTree();
    #define MAX\_OP 10
    for (int i = 0; i < MAX_OP; i++) {
        int val = rand() % 100;
        insert(tree, val);
        output(tree);
    }
    #undef MAX\_OP
    pre_order(tree);
    in_order(tree);
    post_order(tree);
    clear(tree);

    return 0;
}

Node *getNewNode(int val) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->data = val;
    p->lchild = p->rchild = NULL;
    return p;
}

Tree *getNewTree() {
    Tree *t = (Tree *)malloc(sizeof(Tree));
    t->root = NULL;
    t->length = 0;
    return t;
}

// ⼆叉排序树插入操作
// 性质：一颗二叉树中的任何三元组都满足 B(左孩子) < A(根节点) < C (右孩子)的这种关系，故中序遍历可实现排序
// 插入过程（尾插法）：从根节点开始，找到待插入位置前的叶子节点（向下寻找），然后返回各个节点地址（向上回溯）
Node *insert\_node(Node *root, int val, int *flag) {
    if (root == NULL) {
        *flag = 1;
        return getNewNode(val);
    }
    if (root->data == val) return root; // ⼆叉排序树的性质：任何三元组都满足 B(左孩子) < A(根节点) < C (右孩子)
    if (root->data > val) root->lchild = insert_node(root->lchild, val, flag);
    else root->rchild = insert_node(root->rchild, val, flag);
    return root;
}

void insert(Tree *t, int val) {
    if (t == NULL) return ;
    int flag = 0;   // 传出参数，标记当前插入节点是否成功，成功:1，失败:0
    t->root = insert_node(t->root, val, &flag);
    t->length += flag;
    return ;
}

// 前序：根->左->右
void pre\_order\_node(Node *root) {
    if (root == NULL) return ;
    printf("%d ", root->data);
    pre_order_node(root->lchild);
    pre_order_node(root->rchild);
    return ;
}

void pre\_order(Tree *t) {
    if (t == NULL) return ;
    printf("pre\_order : ");
    pre_order_node(t->root);
    printf("\n");
    return ;
}

// 中序：左->根->右
void in\_order\_node(Node *root) {
    if (root == NULL) return ;
    in_order_node(root->lchild);
    printf("%d ", root->data);
    in_order_node(root->rchild);
    return ;
}

void in\_order(Tree *t) {
    if (t == NULL) return ;
    printf("in\_order : ");
    in_order_node(t->root);
    printf("\n");
    return ;
}

// 后序：左->右->根
void post\_order\_node(Node *root) {
    if (root == NULL) return ;
    post_order_node(root->lchild);
    post_order_node(root->rchild);
    printf("%d ", root->data);
    return ;
}

void post\_order(Tree *t) {
    if (t == NULL) return ;
    printf("post\_order : ");
    post_order_node(t->root);
    printf("\n");
    return ;
}

// 从叶子节点开始删除
void clear\_node(Node *node) {
    if (node == NULL) return ;
    clear_node(node->lchild);
    clear_node(node->rchild);
    free(node);
    return ;
}

void clear(Tree *t) {
    if (t == NULL) return ;
    clear_node(t->root);
}

// 相当于前序遍历
void output\_node(Node *root) {
    if (root == NULL) return ;
    printf("%d", root->data);
    if (root->lchild == NULL && root->rchild == NULL) return ;  // 若是叶子节点，则结束
    printf("(");
    output_node(root->lchild);
    printf(",");
    output_node(root->rchild);
    printf(")");
    return ;
}

void output(Tree *t) {
    if (t == NULL) return ;
    printf("tree(%d) : ", t->length);
    output_node(t->root);
    printf("\n");
}
// tree(1) : 6
// tree(2) : 6(,28)
// tree(3) : 6(,28(9,))
// tree(4) : 6(,28(9,87))
// tree(5) : 6(,28(9,87(61,)))
// tree(6) : 6(,28(9,87(61(34,),)))
// tree(7) : 6(,28(9,87(61(34(,40),),)))
// tree(8) : 6(,28(9,87(61(34(,40),65),)))
// tree(9) : 6(,28(9(,20),87(61(34(,40),65),)))
// tree(9) : 6(,28(9(,20),87(61(34(,40),65),)))
// pre\_order : 6 28 9 20 87 61 34 40 65 
// in\_order : 6 9 20 28 34 40 61 65 87 
// post\_order : 20 9 40 34 65 61 87 28 6

3.2 广义表转二叉树

#include 
#include 
#include 

 //⼆叉树的结构定义
typedef struct Node {
    char data;
    struct Node *lchild, *rchild;
} Node;

typedef struct Tree {
    Node *root;
    int length;
} Tree;

//栈的结构定义（存储⼆叉树节点地址）
typedef struct Stack {
    Node **data;    // 定义二级指针的原因：使用数组来存放每个节点的地址，即数组的每个元素都是 Node*
    int top, size;  // top: 标记栈顶位置，默认为-1；size: 当前栈空间的大小
} Stack;

Node *getNewNode(char);             // 节点的初始化
Tree *getNewTree();                 // ⼆叉树的初始化
void clear\_node(Node *);            // 销毁⼆叉树的节点
void clear\_tree(Tree *);            // 销毁⼆叉树
Stack *init\_stack(int);             // 栈的初始化
void clear\_stack(Stack *);          // 栈的销毁
Node *top(Stack *);                 // 输出栈顶元素
int empty(Stack *);                 // 栈的判空
int push(Stack *, Node *);          // 压栈操作
int pop(Stack *);                   // 弹栈操作
void pre\_order\_node(Node *);
void pre\_order(Tree *);             // 前序遍历
void in\_order\_node(Node *);
void in\_order(Tree *);              // 中序遍历
void post\_order\_node(Node *);
void post\_order(Tree *);            // 后序遍历
Node *build(const char *, int *);   // 构建一颗二叉树

int main() {
    char str[1000] = { 0 };
    int node_num = 0;
    scanf("%[^\n]s", str);
    getchar();
    Tree *tree = getNewTree();
    tree->root = build(str, &node_num);
    tree->length = node_num;
    pre_order(tree);
    in_order(tree);
    post_order(tree);
    clear_tree(tree);

    return 0;
}

Node *getNewNode(char val) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->lchild = p->rchild = NULL;
    p->data = val;
    return p;
}

Tree *getNewTree() {
    Tree *t = (Tree *)malloc(sizeof(Tree));
    t->root = NULL;
    t->length = 0;
    return t;
}

void clear\_node(Node *root) {
    if (root == NULL) return;
    clear_node(root->lchild);
    clear_node(root->rchild);
    free(root);
    return;
}

void clear\_tree(Tree *t) {
    if (t == NULL) return;
    clear_node(t->root);
    free(t);
    return;
}

Stack *init\_stack(int n) {
    Stack *s = (Stack *)malloc(sizeof(Stack));
    s->data = (Node **)malloc(sizeof(Node *) * n);
    s->top = -1;
    s->size = n;
    return s;
}

void clear\_stack(Stack *s) {
    if (s == NULL) return;
    free(s->data);
    free(s);
    return;
}

Node *top(Stack *s) {
    return s->data[s->top];
}

int empty(Stack *s) {
    return s->top == -1;
}

int push(Stack *s, Node *val) {
    if (s == NULL) return 0;
    if (s->top == s->size - 1) return 0;
    s->data[++(s->top)] = val;
    return 1;
}

int pop(Stack *s) {
    if (s == NULL) return 0;
    if (empty(s)) return 0;
    s->top -= 1;
    return 1;
}

// 二叉树的广义表表示：str = "A(B(, D), C(E))"
// '(': 根节点入栈，设置flag=0; ')': 出栈; ',': 设置flag=1;
// flag=0: 表示是左子节点, flag=1: 表示是右子节点
// 将广义表转化为二叉树
// 前序|后续遍历 && 中序遍历 ==> 二叉树
// 本方法：栈实现广义表转二叉树
// 方法2：系统栈（递归）实现广义表转二叉树
Node *build(const char *str, int *node\_num) {
    Stack *s = init_stack(strlen(str));
    int flag = 0;
    Node *temp = NULL, *p = NULL;   // temp：指向每层的父节点，p：指向根节点
    while (str[0]) {
        switch (str[0]) {
        case '(':
            push(s, temp);
            flag = 0;
            break;
        case ')':
            p = top(s);
            pop(s);
            break;
        case ',': flag = 1; break;
        case ' ': break;
        default:
            temp = getNewNode(str[0]);
            if (!empty(s) && flag == 0) {
                top(s)->lchild = temp;
            }
            else if (!empty(s) && flag == 1) {
                top(s)->rchild = temp;
            }
            ++(*node_num);
            break;
        }
        ++str;
    }
    clear_stack(s);
    if (temp && p == NULL) p = temp;    // 只有根节点的情况
    return p;
}

void in\_order\_node(Node *root) {
    if (root == NULL) return;
    in_order_node(root->lchild);
    printf("%c ", root->data);
    in_order_node(root->rchild);
    return;
}

void in\_order(Tree *tree) {
    if (tree == NULL) return;
    printf("in\_order(%d) : ", tree->length);
    in_order_node(tree->root);
    printf("\n");
    return;
}

void pre\_order\_node(Node *root) {
    if (root == NULL) return;
    printf("%c ", root->data);
    pre_order_node(root->lchild);
    pre_order_node(root->rchild);
    return;
}

void pre\_order(Tree *tree) {
    if (tree == NULL) return;
    printf("pre\_order(%d) : ", tree->length);
    pre_order_node(tree->root);
    printf("\n");
    return;
}

void post\_order\_node(Node *root) {
    if (root == NULL) return;
    post_order_node(root->lchild);
    post_order_node(root->rchild);
    printf("%c ", root->data);
    return;
}

void post\_order(Tree *tree) {
    if (tree == NULL) return;
    printf("post\_order(%d) : ", tree->length);
    post_order_node(tree->root);
    printf("\n");
    return;
}

转载请注明：xuhss » 二叉树的创建、遍历、广义表转换