? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
在实际应用中DQN会引起高估,进而影响动作的正确选择。本文介绍的高估问题解决办法为:Target Network & Double DQN.
11. Target Network & Double DQN
11.1 Bootstraps \ 自举
自举通俗来说就是自己把自己举起来,这在现实物理学中是很荒唐的,但在统计学和强化学习中是可以做到自举的。
在强化学习中,自举 的意思是用一个估算去更新同类的估算,即自己把自己举起来。
之前我们提到:
- 用 transition (st,at,rt,st+1)(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1}) 更新一次 w。
- TD target: yt=rt+γ⋅maxaQ(st+1,a;w)yt=rt+γ⋅maxaQ(st+1,a;w)y_t = {r_t} + \gamma \cdot \mathop{max}\limits_{a} Q({s_{t+1}},{a};w)
- TD error: δt=Q(st,at;w)−ytδt=Q(st,at;w)−yt\delta_t = Q({s_t},{a_t};w) - y_t
- 梯度下降,更新参数: w←w−α⋅δt⋅∂Q(st,at;w)∂ww←w−α⋅δt⋅∂Q(st,at;w)∂ww \leftarrow w -\alpha \cdot \delta_t \cdot \frac{\partial Q({s_t},{a_t};w)}{\partial w}
我们注意一下TD target,ytyty_t 中含有部分真实 也含有 部分DQN 在 t+1 时刻的估计。而梯度下降中的 δtδt\delta_t 中含有 ytyty_t 。
这说明我们为了更新 t 时刻的估计,而用到了 t+1 时刻的预测。
这就是一个估计值更新其本身,也就是自己把自己举起来,bootstraping.
11.2 Overestimation
用TD算法训练DQN,会导致DQN往往高估真实的动作价值;下面来介绍一下 高估问题产生的原因。
- 计算TD target 使用了最大化 max,使得 TD target 比真实的动作价值大。
- Bootstrapping,用自己的估计更新自己,高估引发更离谱的高估;

回到顶部#### a. 最大化
举个例子来说明为什么使用最大化会产生高估:
假设我们观测到了任意 n 个实数 x1,x2,...,xnx1,x2,...,xnx_1,x_2,...,x_n;向其中加入均值是 0 的噪声,得到 Q1,Q2,...,QnQ1,Q2,...,QnQ_1,Q_2,...,Q_n;
加入噪声这件事会造成:
- 均值不变,即:E[meani(Qi)]=meani(xi)E[meani(Qi)]=meani(xi)E[mean_i(Q_i)]=mean_i(x_i);
- 最大值的均值更大,即:E[maxi(Qi)]≥maxi(xi)E[maxi(Qi)]≥maxi(xi)E[max_i(Q_i)]\geq max_i(x_i);
- 最小值的均值更小,即:E[mini(Qi)]≤mini(xi)E[mini(Qi)]≤mini(xi)E[min_i(Q_i)]\leq min_i(x_i)
这些结论可以自己带入数字验证,都有相关的定理支撑。
简单的解释是,加入噪声从信号图的角度来讲,让上下限更宽,所以有以上结论。
下面来看看这个原理投射在TD 算法上的:
- 真实的动作价值为(虽然我们不知道,但是其存在):x(a1),...,x(an)x(a1),...,x(an)x(a_1),...,x(a_n)
- 我们用DQN估算真实的动作价值,噪声就是由 DQN 产生的:Q(s,a1;w),...,Q(s,an;w)Q(s,a1;w),...,Q(s,an;w)Q(s,a_1;w),...,Q(s,a_n;w);
- 如果 DQN 对于真实价值的估计是 无偏的,那么 误差 就相当于上文的均值为0的 噪声 ;
meana(x(a))=meana(Q(s,a;w))meana(x(a))=meana(Q(s,a;w))\mathop{mean}\limits_{a} (x(a)) = \mathop{mean}\limits_{a} (Q(s,a;w))
- 而根据上面的举例,maxaQ(s,a;w)≥maxa(x(a))maxaQ(s,a;w)≥maxa(x(a))\mathop{max} \limits_{a} Q(s,a;w)\geq \mathop{max} \limits_{a}(x(a));意思就是,DQN的预测q: maxaQ(s,a;w)maxaQ(s,a;w)\mathop{max} \limits_{a} Q(s,a;w),是对真实情况的高估。
- 那么,根据 yt=rt+γ⋅qt+1yt=rt+γ⋅qt+1y_t = {r_t} + \gamma \cdot q_{t+1},ytyty_t 较真实情况也高估了。
- TD 算法本身的思想就是,让预测接近 TD target,更新之后的 DQN 预测也会高估。
回到顶部#### b. 自举
- TD target 用到了 t+1 时刻的估计:qt+1=maxaQ∗(st+1,a;w)qt+1=maxaQ∗(st+1,a;w)q_{t+1}=\mathop{max}\limits_{a} Q^*({s_{t+1}},{a};w);
-
而使用 TD target 在 t+1 时刻的估计 qt+1qt+1q_{t+1} 来更新 t 时刻的估计,用DQN 来更新 DQN 自己,这样 bootstrapping 会导致高估更严重:
- 向高估方向连续进行了两次运算,
yt=rt+γ⋅maxaQ(st+1,a;w)yt=rt+γ⋅maxaQ(st+1,a;w)y_t = {r_t} + \gamma \cdot \mathop{max}\limits_{a} Q({s_{t+1}},{a};w),分别是:
1. Q 处就是 DQN 对 t+1 时刻的高估 2. 在计算 ytyty\_t 的时候,最大化又导致了高估 3. 两次高估是同向的; 4. 通过TD 算法将这种高估传播回 DQN,DQN的高估更严重了 5. 循环往复,正反馈
回到顶部#### c. 高估为什么有害
回顾 DQN / 价值学习 的基本思想:在当前状态 ststs_t 的情况下,通过DQN输出各个动作的分数,从中挑选分数相对最高的动作执行。
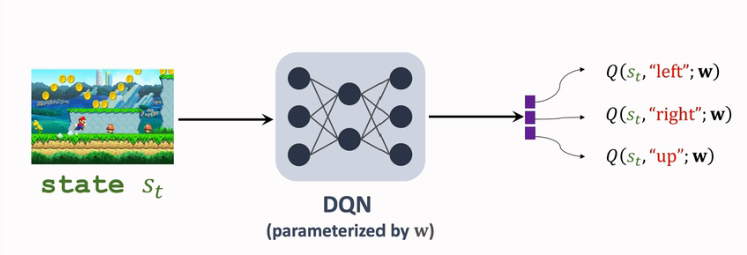
如果高估这个现象对于所有动作是均匀的,那么不影响本该被选中的动作被选中。所以高估本身没有问题,有害的是不均匀的高估。
实际上 DQN 的高估就是非均匀的:
- 使用一个transition (st,at,rt,st+1)(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1}) 去更新 w;
- TD target ytyty_t现在高估了真实情况
- TD 算法鼓励 QDN 的预测接近 ytyty_t,
- 那么更新参数后,TD 算法把 QDN 对于Q-star的估值推高
- 所以,重点来了,当某组 transition(包含状态和动作 s&a 的二元组) 每被用来更新一次DQN,就会让DQN倾向于高估s和a的价值;
- 而这个二元组在 Reply Buffer 中的频率不均匀,这种不均匀导致高估的不均匀。
11.3 解决方案
介绍高估问题的两种解决方案:
- 第一种是避免 Bootstrapping ,即不要用 DQN 自己的 TD target 跟新DQN,而是使用另一个神经网络 Target Network。
- 另一种思路是用Double DQN,用来缓解最大化造成的高估;虽然也使用 Target Network,但用法有所不同。
回到顶部#### a. Target Network
这里我们引入 另一个神经网络 Target Network Q(s,a,w−)Q(s,a,w−)Q(s,a,w^-),TN 的结构与 DQN 一样,但是参数 www 不同。另外两者的用途也不同,DQN用来收集 transitions,控制 agent 运动,而 TN 只用来 计算 TD target。
将 TN 用在 TD 算法上:
- 用 Target Network 更新 TD Target:yt=rt+γ⋅ maxaQ(st+1,a;w−)yt=rt+γ⋅ maxaQ(st+1,a;w−)y_t = r_t + \gamma\cdot \ \mathop{max}\limits_{a} Q(s_{t+1},a;w^-)
- DQN 计算TD error:δt=Q(st,at;w)−ytδt=Q(st,at;w)−yt\delta_t = Q({s_t},{a_t};w) - y_t
- 梯度下降更新参数: w←w−α⋅δt⋅∂Q(st,at;w)∂ww←w−α⋅δt⋅∂Q(st,at;w)∂ww \leftarrow w -\alpha \cdot \delta_t \cdot \frac{\partial Q({s_t},{a_t};w)}{\partial w}
注意这里更新的是 DQN 的 w,没有更新 TN 的 w−w−w^-
- w−w−w^- 每隔一段时间更新,更新方式有很多种:
* 直接: w−←ww−←ww^-\leftarrow w
* 加权平均:w−←τ⋅w+(1−τ)⋅w−w−←τ⋅w+(1−τ)⋅w−w^-\leftarrow \tau\cdot w + (1-\tau)\cdot w^-由于 TN 还是需要 DQN 的参数,不是完全独立,所以不能完全避免Bootstrapping.
回到顶部#### b. Double DQN
原始算法:
- 计算TD target 的第一步是选择:a∗=argmaxaQ(st+1,a;w)a∗=argmaxaQ(st+1,a;w)a^*=\mathop{argmax}\limits_{a} Q(s_{t+1},a;w),这一步是使用 DQN自己;
- 计算 yt=rt+γ⋅maxaQ(st+1,a∗;w)yt=rt+γ⋅maxaQ(st+1,a∗;w)y_t = {r_t} + \gamma \cdot \mathop{max}\limits_{a} Q({s_{t+1}},{a^*};w)
- 这种算法最差
使用 TN:
- 计算TD target 的第一步是选择:a∗=argmaxaQ(st+1,a;w−)a∗=argmaxaQ(st+1,a;w−)a^*=\mathop{argmax}\limits_{a} Q(s_{t+1},a;w^-),这一步是使用 TN;
- 计算 yt=rt+γ⋅Q(st+1,a∗;w−)yt=rt+γ⋅Q(st+1,a∗;w−)y_t = {r_t} + \gamma \cdot Q({s_{t+1}},{a^*};w^-)
- 较于第一种较好,但仍存在高估;
Double DQN:
- 选择:a∗=argmaxaQ(st+1,a;w)a∗=argmaxaQ(st+1,a;w)a^*=\mathop{argmax}\limits_{a} Q(s_{t+1},a;w),注意这一步是 Double DQN;
- 计算:yt=rt+γ⋅Q(st+1,a∗;w−)yt=rt+γ⋅Q(st+1,a∗;w−)y_t = {r_t} + \gamma \cdot Q({s_{t+1}},{a^*};w^-);这一步使用 TN;
- 可见改动非常小,但是改进效果显著。(没有消除高估)
为什么呢?
Q(st+1,a∗;w−)≤maxaQ(st+1,a;w−)Q(st+1,a∗;w−)≤maxaQ(st+1,a;w−)Q(s_{t+1},a^*;w^-)\leq \mathop{max}\limits_{a}Q(s_{t+1},a;w^-)
- 因为右边是求了最大化,所以右边一定比左边大;
- 而左边是 Double DQN作出的估计,右边是 TN 算出来的;
- 这个式子说明: Double DQN 作出的估计更小,所以缓解了 高估问题;
x. 参考教程
- 视频课程:深度强化学习(全)_哔哩哔哩_bilibili
- 视频原地址:https://www.youtube.com/user/wsszju
- 课件地址:https://github.com/wangshusen/DeepLearning
转载请注明:xuhss » 强化学习-学习笔记11 | 解决高估问题