? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
本系列的完结篇,介绍了连续控制情境下的强化学习方法,确定策略 DPG 和随机策略 AC 算法。
15. 连续控制
15.1 动作空间
-
离散动作空间
- Action space A=left,right,upAction space A=left,right,upAction \ space \ \mathcal{A}={left,right,up}
- 比如超级玛丽游戏中的向上\向左\向右;
- 此前博文讨论的,都是离散的控制,动作有限。
-
连续动作空间
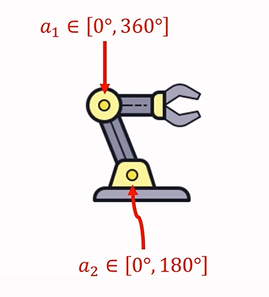
- Action space A=[0°,360°]×[0°,180°]Action space A=[0°,360°]×[0°,180°]Action \ space \ \mathcal{A}=[0°,360°]×[0°,180°]
- 比如机械臂,如果具有两个运动关节:
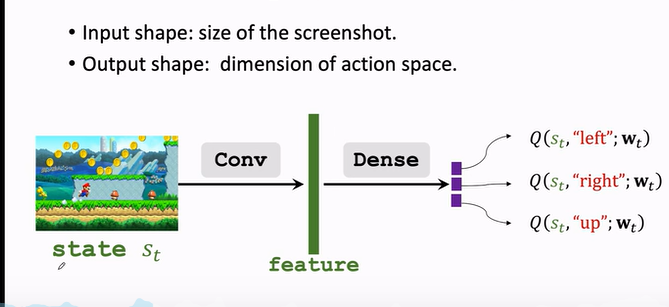
- 价值网络 DQN 可以解决离散动作控制的问题,因为 DQN 输出的是有限维度的向量。
- 策略网络也同样。
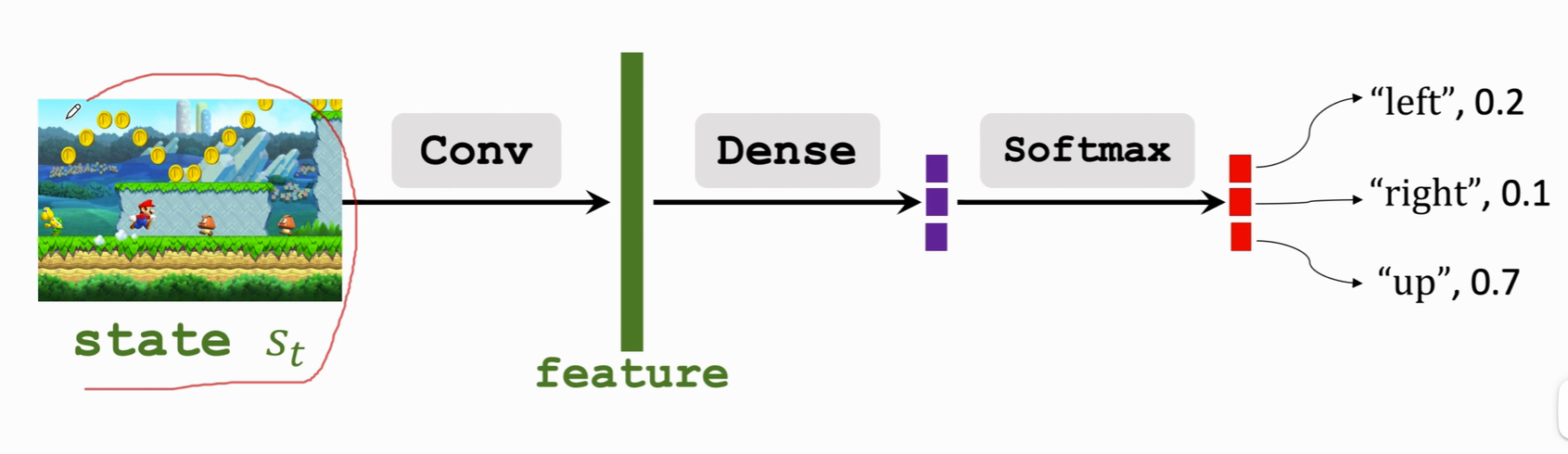
- 所以此前的方法不能简单照搬到连续控制。要想应用到连续控制上,可以采用 连续空间离散化。
连续空间离散化:
- 比如机械臂进行二维网格划分。那么有多少个格子,就有多少种动作。
- 缺点:假设d为连续动作空间的自由度,动作离散化后的数量会随着d的增加呈现指数增长,从而造成维度灾难。动作太多会学不好DQN 或 策略网络。
- 所以 离散化 适合自由度较小的问题。
另外还有两个方法:
- 使用确定策略网络(Deterministic policy networkDeterministic policy networkDeterministic \ policy \ network)
- 使用随机策略(Stochastic policy networkStochastic policy networkStochastic \ policy \ network)。
15.2 DPG | 确定策略
回到顶部#### a. 基础了解
Deterministic Policy Gradient.确定策略梯度,可以用于解决连续控制问题。后续引入深度神经网络,就是著名的 DDPG。
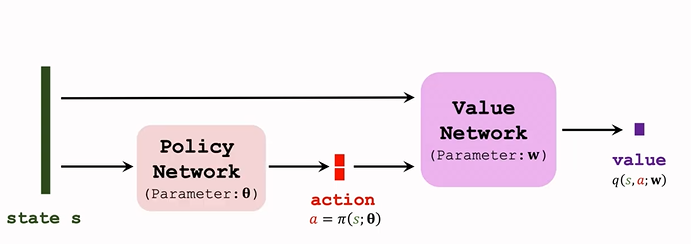
DPG 是 Actor-Critic 方法的一种。结构图如下:
-
策略网络 actor
- 策略网络是确定性的函数 a=π(s;θ)a=π(s;θ)a=\pi(s;\theta)
- 输入是状态 s ;输出是一个具体的动作 s;即给定状态输出具体的动作,无随机性。
- 输出的动作是可以指导运动的实数或向量。
-
价值网络 critic
- 记作 q(s,a;w)q(s,a;w)q(s,a;w)
- 输入是状态 s 和 动作 a,基于状态 s,评价动作 a 的好坏程度,输出一个分数 q;
- 训练两个神经网络,让两个网络越来越好。
-
用 TD 算法更新 价值网络:
- 观测 transition:(st,at,rt,st+1)(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1})
- 价值网络预测 t 时刻 的动作价值 qt=q(st,at;w)qt=q(st,at;w)q_t=q(s_t,a_t;w)
- 价值网络预测 t+1时刻的价值:qt+1=q(st+1,a′t+1;w)qt+1=q(st+1,at+1′;w)q_{t+1}=q(s_{t+1},a'_{t+1};w)
注意这里的 a′t+1at+1′a'_{t+1} 是 策略网络 t+1 时刻预选出来的动作,尚未执行。
- TD error:δt=qt−(rt+γ⋅qt+1)TD targetδt=qt−(rt+γ⋅qt+1)⏟TD target\delta_t=q_t-\underbrace{(r_t+\gamma\cdot q_{t+1})}_{TD \ target}
- 更新参数:w←w−α⋅δt⋅∂q(st,at;w)∂ww←w−α⋅δt⋅∂q(st,at;w)∂ww\leftarrow w-\alpha\cdot\delta_t \cdot \frac{\partial q(s_t,a_t;w)}{\partial w}
- 策略网络用 DPG 算法 更新
回到顶部#### b. 算法推导
对 DPG 算法进行推导。
- 训练价值网络的目标是,让价值网络的输出 q 越大越好。
- 而在DPG 的网络结构中,在给定状态时,动作是确定的(策略网络会给出一个确定的动作),且价值网络固定,那么影响输出的就是策略网络的参数 θθ\theta。
- 所以更新 θ 使价值 q 更大;
- 计算价值网络关于 θ 的梯度 DPG:g=∂q(s,π(s;θ))∂θ=∂a∂θ⋅∂q(s,a;w)∂ag=∂q(s,π(s;θ))∂θ=∂a∂θ⋅∂q(s,a;w)∂ag=\frac{\partial q(s,\pi(s;\theta))}{\partial\theta}=\frac{\partial a}{\partial\theta}\cdot\frac{\partial q(s,a;w)}{\partial a}
链式法则,让梯度从价值 q 传播到动作 a;再从 a 传播到策略网络。
- 梯度上升更新 θθ\theta:θ←θ+β⋅gθ←θ+β⋅g\theta\leftarrow \theta+\beta\cdot g
回到顶部#### c. 算法改进1 | 使用 TN
上面的 DPG 是比较原始的版本,用 Target Network 可以提升效果。Target Network 在此前第11篇中讲过,上文中的算法也会出现高估问题或者低估问题。
因为用自身下一时刻的估计来更新此时刻的估计。
Target Network 方法的过程是:
- 用 价值网络 计算 t 时刻的价值: qt=q(st,qt;w)qt=q(st,qt;w)q_t=q(s_t,q_t;w)
- TD target (不同之处):
- 改用两个不同的神经网络计算 TD target 。
- 用 target policy network 代替 策略网络 来预选 a′t+1at+1′a'_{t+1},网络结构和策略网络一样,但参数不一样;记为 a′t+1=π(ss+1;θ−)at+1′=π(ss+1;θ−)a'_{t+1}=\pi(s_{s+1};\theta^-)
- 用 target value network 代替 价值网络 计算 qt+1qt+1q_{t+1},与价值网络结构相同,参数不同;记为 qt+1=q(st+1,a′t+1;w−)qt+1=q(st+1,at+1′;w−)q_{t+1}=q(s_{t+1},a'_{t+1};w^-)
- 后续 TD error 以及 参数更新 与 原始算法一致,具体见第11篇
回到顶部#### d. 完整过程
- 策略网络做出选择:a=π(s;θ)a=π(s;θ)a=\pi(s;\theta)
- 用 DPG 更新 策略网络:θ←θ+β⋅∂a∂θ⋅∂q(s,a;w)∂aθ←θ+β⋅∂a∂θ⋅∂q(s,a;w)∂a\theta\leftarrow \theta+ \beta\cdot\frac{\partial a}{\partial\theta}\cdot\frac{\partial q(s,a;w)}{\partial a}
- 价值网络计算 qtqtq_t:qt=q(s,a;w)qt=q(s,a;w)q_t=q(s,a;w)
- Target Networks 计算 qt+1qt+1q_{t+1}
- TD error:δt=qt−(rt+γ⋅qt+1)δt=qt−(rt+γ⋅qt+1)\delta_t=q_t-(r_t+\gamma\cdot q_{t+1})
- 梯度下降:w←w−α⋅δt⋅∂q(s,a;w)∂ww←w−α⋅δt⋅∂q(s,a;w)∂ww\leftarrow w-\alpha\cdot\delta_t \cdot\frac{\partial q(s,a;w)}{\partial w}
同样,之前讲过的其他改进也可以用于这里,如经验回放、multi-step TD Target 等。
15.3 确定策略 VS 随机策略
DPG 使用的是 确定策略网络,跟之前的随机策略不同。
| \ | 随机策略 | 确定策略 |
|---|---|---|
| 策略函数 | $\pi(a | s;\theta)$ |
| 输出 | 每个动作一个概率值,向量 | 确定的动作 |
| 控制方式 | 根据概率分布抽样a | 输出动作并执行 |
| 应用 | 大多是离散控制,用于连续的话结构大有不同 | 连续控制 |
15.4 | 随机策略
这部分来介绍怎么在连续控制问题中应用随机策略梯度。
构造一个策略网络,来做连续控制,这个策略网络与之前学过的相差很大,以机械臂为例:
回到顶部#### a. 自由度为 1 的连续动作空间
先从一个简单的情况研究起,自由度为1,这时动作都是实数 A⊂RA⊂R\mathcal{A}\subset \mathbb{R}
- 记均值为 μμ\mu,标准差是 σσ\sigma ,都是状态 s 的函数,输出是一个实数
- 假定我们的策略函数是正态分布函数N(μ,σ2)N(μ,σ2)N(\mu,\sigma^2):π(a|s)=16.28√σ⋅exp(−(a−μ)22σ2)π(a|s)=16.28σ⋅exp(−(a−μ)22σ2)π(a|s)=\frac{1}{\sqrt{6.28}\sigma}\cdot exp(-\frac{(a-\mu)^2}{2\sigma^2})
- 根据策略函数随机抽样一个动作
回到顶部#### b. 自由度 >1 的连续动作空间
而机械臂的自由度通常是3或者更高,把自由度记为 d,动作 a 是一个 d 维的向量。
- 用粗体 μμ\boldsymbol{\mu} 表示均值,粗体 σσ\boldsymbol{\sigma} 表示标准差,都是状态 s 的函数,输出是都是 d 维向量
- 用 μiμi\mu_i 和 σiσi\sigma_i 表示 μ(s)μ(s)\boldsymbol{\mu}(s) 和 σ(s)σ(s)\boldsymbol{\sigma}(s) 输出的第 i 个元素,假设各个维度独立,则可以表示成 a 中的函数连乘
- π(a|s)=Πdi=116.28√σi⋅exp(−(ai−μi)22σ2i)π(a|s)=Πi=1d16.28σi⋅exp(−(ai−μi)22σi2)π(a|s)=\Pi_{i=1}^d \frac{1}{\sqrt{6.28}\sigma_i}\cdot exp(-\frac{(a_i-\mu_i)^2}{2\sigma_i^2})
但是问题是,我们不知道 具体的 μ,σμ,σ\mu , \sigma,我们用神经网络来近似它们。
回到顶部#### c. 函数近似
- 用神经网络 μ(s;θμ)μ(s;θμ)\mu(s;\theta^\mu) 近似 μμ\mu
用神经网络 σ(s;θσ)σ(s;θσ)\sigma(s;\theta^\sigma)近似 σ(s)σ(s)\sigma(s),实际上这样效果并不好,近似方差的对数更好:ρi=lnσ2i,for i=1,...,d.ρi=lnσi2,for i=1,...,d.\boldsymbol{\rho_i=ln\sigma_i^2},for \ i=1,...,d.- 即用神经网络 ρ(s;θρ)ρ(s;θρ)\boldsymbol\rho(s;\boldsymbol{\theta^\rho}) 近似 ρρ\boldsymbol\rho;
网络结构如下:
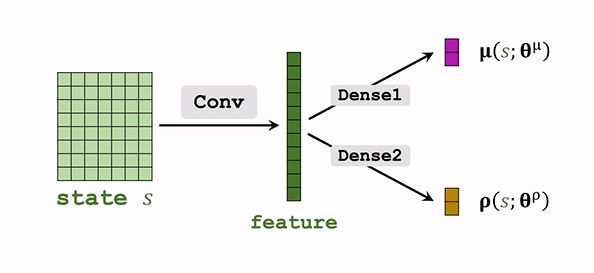
回到顶部#### d. 连续控制
- 观测到 状态 s,输入神经网络;
- 神经网络输出 μ^=μ(s;θμ),ρ^=ρ(s;θρ)μ^=μ(s;θμ),ρ^=ρ(s;θρ)\hat\mu=\mu(s;\theta^\mu),\hat\rho=\rho(s;\theta^\rho),都是 d 维度
- ρ^ρ^\hat\rho 计算 σ^2i=exp(ρ^i)σ^i2=exp(ρ^i)\hat\sigma_i^2=\exp(\hat\rho_i)
- 随机抽样得到动作 a :ai∼N(μ^i,σ^2i)ai∼N(μ^i,σ^i2)a_i\sim\mathcal{N}(\hat\mu_i,\hat\sigma_i^2)
这个正态分布是假定的策略函数。
回到顶部#### e. 训练策略网络
1. 辅助神经网络
Auxiliary Network, 计算策略梯度时对其求导。
- 随机策略梯度为:g(a)=∂lnπ(a|s;θ)∂θ⋅Qπ(s,a)g(a)=∂lnπ(a|s;θ)∂θ⋅Qπ(s,a)g(a)=\frac{\partial ln\pi(a|s;\theta)}{\partial\theta}\cdot Q_\pi(s,a)
- 计算 ππ\pi 的对数。
- 策略网络为:π(A|s;θμ)=Πdi=116.28√⋅exp(−(ai−−μ)22δ2i)π(A|s;θμ)=Πi=1d16.28⋅exp(−(ai−−μ)22δi2)\pi(A|s;\theta^\mu)=\Pi_{i=1}^d\frac{1}{\sqrt{6.28}}\cdot\exp(-\frac{(a_i--\mu)^2}{2\delta^2_i}),输出是一个概率密度,表示在某点附近的可能性大小
虽然可以算出来某个动作的概率,但实际上我们只需要知道 均值 和 方差,来做随机抽样即可,所以实际上我们用不到这个策略函数 ππ\pi
- 由上面策略梯度公式知:我们需要策略 ππ\pi 的对数,所以训练时,我们会用到策略 ππ\pi 的对数,而不是 ππ\pi 本身:
lnπ(a|s;θμ,θρ)=∑i=1d[−lnδi−(ai−μi)22δ2]+constlnπ(a|s;θμ,θρ)=∑i=1d[−lnδi−(ai−μi)22δ2]+const\ln\pi(a|s;\theta^\mu,\theta^\rho)=\sum_{i=1}^d[-\ln\delta_i-\frac{(a_i-\mu_i)^2}{2\delta^2}]+const
- 由于神经网络输出的时方差对数ρiρi\rho_i,而不是δ2iδi2\delta^2_i,所以做个替换:δ2i=expρiδi2=expρi\delta_i^2=\exp\rho_i
- lnπ(a|s;θμ,θρ)=∑di=1[−lnδi−(ai−μi)22δ2]+const=∑di=1[−ρi2−(ai−μi)22exp(ρi)]+constlnπ(a|s;θμ,θρ)=∑i=1d[−lnδi−(ai−μi)22δ2]+const=∑i=1d[−ρi2−(ai−μi)22exp(ρi)]+const\ln\pi(a|s;\theta^\mu,\theta^\rho)=\sum_{i=1}^d[-\ln\delta_i-\frac{(a_i-\mu_i)^2}{2\delta^2}]+const\=\sum_{i=1}^d[-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\exp(\rho_i)}]+const
- 这样 神经网络的对数 就表示成了 ρ,μρ,μ\rho,\mu 的形式,记 θ=(θμ,θρ)θ=(θμ,θρ)\theta=(\theta^\mu,\theta^\rho)
-
把上式连加的一项记为 f(s,a;θ)f(s,a;θ)f(s,a;\theta),这就是辅助神经网络 Auxiliary Network.用于帮助训练。
- f(a,s;θ)=∑di=1[−ρi2−(ai−μi)22exp(ρi)]f(a,s;θ)=∑i=1d[−ρi2−(ai−μi)22exp(ρi)]f(a,s;\theta)=\sum_{i=1}^d[-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\exp(\rho_i)}]
- f 的输入是 s, a ,依赖于 ρ,μρ,μ\rho,\mu,所以参数也是 θθ\theta
- 结构如下:
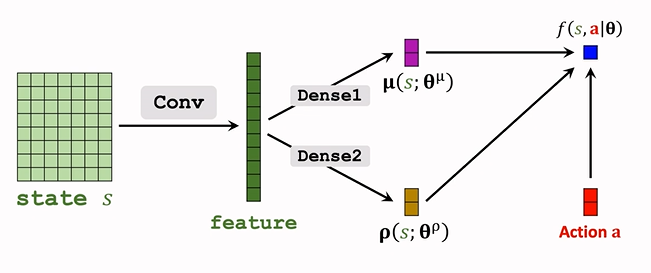
1. 输入为 μ,ρs,aμ,ρ⏟s,a\underbrace{\mu,\rho}\_{s},a,输出为一个实数 f; 2. f 依赖于卷积层和全连接层的参数,所以接下来反向传播,可以算出 f 关于全连接层 Dense 参数的梯度,再算出 关于卷积层参数的梯度: 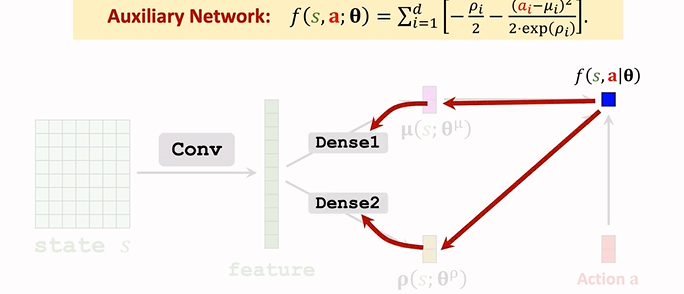 用 ∂f∂θ∂f∂θ\frac{\partial f}{\partial \theta} 来表示梯度。
2.策略梯度算法训练策略网络
- 随机策略梯度:g(a)=∂lnπ(a|s;θ)∂θ⋅Qπ(s,a)g(a)=∂lnπ(a|s;θ)∂θ⋅Qπ(s,a)g(a)=\frac{\partial ln\pi(a|s;\theta)}{\partial\theta}\cdot Q_\pi(s,a)
- 辅助神经网路:f(s,a;θ)=lnπ(a|s;θ)+constf(s,a;θ)=lnπ(a|s;θ)+constf(s,a;\theta)=\ln\pi(a|s;\theta)+const
- 可以注意到,f 的梯度和 lnπlnπ\ln\pi 的梯度相同,可以用前者梯度代替后者,即
g(a)=∂f(s,a;θ)∂θ⋅Qπ(s,a)g(a)=∂f(s,a;θ)∂θ⋅Qπ(s,a)g(a)=\frac{\partial f(s,a;\theta)}{\partial \theta}\cdot Q_\pi(s,a)
而 f 作为一个神经网路,成熟的 pytorch 等可以对其自动求导。
-
Q 还未知,需对其做近似
- 具体参见 第14篇
- Reinforce
- 用观测到的回报 ututu_t 来近似 QπQπQ_\pi
- 更新策略网络:θ←θ+β⋅∂f(s,a;θ)∂θ⋅utθ←θ+β⋅∂f(s,a;θ)∂θ⋅ut\theta\leftarrow\theta+\beta\cdot\frac{\partial f(s,a;\theta)}{\partial\theta}\cdot u_t
- Actor-Critic(A2C)
- 用价值网络 q(s,a;w)q(s,a;w)q(s,a;w) 近似 QπQπQ_\pi
- 更新策略网络:θ←θ+β⋅∂f(s,a;θ)∂θ⋅q(s,a;w)θ←θ+β⋅∂f(s,a;θ)∂θ⋅q(s,a;w)\theta\leftarrow\theta+\beta\cdot\frac{\partial f(s,a;\theta)}{\partial\theta}\cdot q(s,a;w)
- 而新引入的价值网络 q(S,a;w)q(S,a;w)q(S,a;w),用 TD 算法来进行学习。
15.5 总结
- 连续动作空间有无穷多种动作数量
-
解决方案包括:
- 离散动作空间,使用标准DQN或者策略网络进行学习,但是容易引起维度灾难
- 使用确定策略网络进行学习
没有随机性,某些情境下不合适。
- 随机策略网络(μμ\mu 与 σ2σ2\sigma^2)
-
随机策略的训练过程:
- 构造辅助神经网络 f(s,a;θ)f(s,a;θ)f(s,a;\theta) 计算策略梯度;
- 策略梯度近似算法包括:reinforce、Actor-Critic 算法
- 可以改进 reinforce 算法,使用带有 baseline 的 reinforce 算法
- 可以改进 Actor-Critic 算法,使用 A2C 算法
本系列完结撒花!
x. 参考教程
- 视频课程:深度强化学习(全)_哔哩哔哩_bilibili
- 视频原地址:https://www.youtube.com/user/wsszju
- 课件地址:https://github.com/wangshusen/DeepLearning
- 参考博客:https://blog.csdn.net/Cyrus_May/article/details/124137445
转载请注明:xuhss » 强化学习-学习笔记15 | 连续控制