文章目录
显示
? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
详细描述
快速排序通过一趟排序将待排序列分割成独立的两部分,其中一部分序列的关键字均比另一部分序列的关键字小,则可分别对这两部分序列继续进行排序,以达到整个序列有序的目的。
快速排序详细的执行步骤如下:
- 从序列中挑出一个元素,称为 “基准”(pivot);
- 重新排序序列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于序列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子序列和大于基准值元素的子序列排序。
算法图解
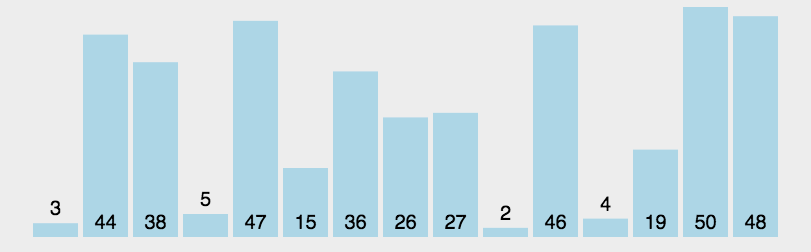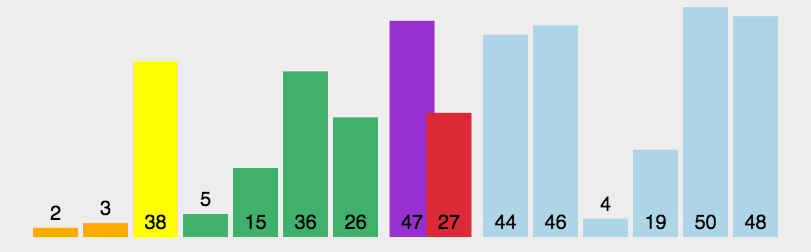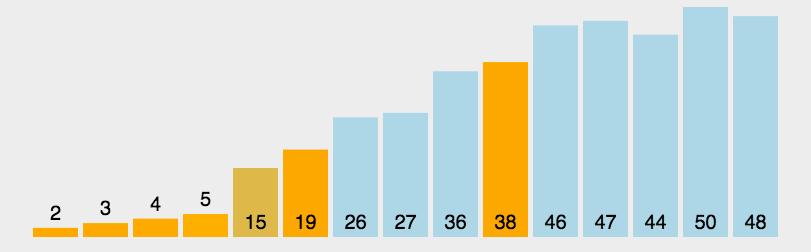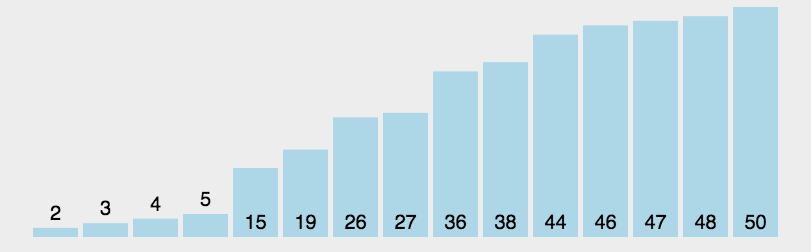
问题解疑
快速排序可以怎样选择基准值?
第一种方式:固定位置选择基准值;在整个序列已经趋于有序的情况下,效率很低。
第二种方式:随机选取待排序列中任意一个数作为基准值;当该序列趋于有序时,能够让效率提高,但在整个序列数全部相等的时候,随机快排的效率依然很低。
第三种方式:从区间的首、尾、中间,分别取出一个数,然后对比大小,取这 3 个数的中间值作为基准值;这种方式解决了很多特殊的问题,但对于有很多重复值的序列,效果依然不好。
快速排序有什么好的优化方法?
首先,合理选择基准值,将固定位置选择基准值改成三点取中法,可以解决很多特殊的情况,实现更快地分区。
其次,当待排序序列的长度分割到一定大小后,使用插入排序。对于待排序的序列长度很小或基本趋于有序时,插入排序的效率更好。
在排序后,可以将与基准值相等的数放在一起,在下次分割时可以不考虑这些数。对于解决重复数据较多的情况非常有用。
在实现上,递归实现的快速排序在函数尾部有两次递归操作,可以对其使用尾递归优化(简单地说,就是尾位置调用自身)。
代码实现
| | package cn.fatedeity.algorithm.sort; |
| | |
| | import java.util.Random; |
| | |
| | /** |
| | * 快速排序算法 |
| | */ |
| | public class QuickSort { |
| | private static void swap(int[] numbers, int src, int target) { |
| | int temp = numbers[src]; |
| | numbers[src] = numbers[target]; |
| | numbers[target] = temp; |
| | } |
| | |
| | private static int[] sort(int[] numbers, int low, int high) { |
| | if (low > high) { |
| | return numbers; |
| | } |
| | // 随机数取基准值 |
| | Random random = new Random(); |
| | int pivotIndex = random.nextInt(low, high + 1); |
| | int pivot = numbers[pivotIndex]; |
| | swap(numbers, pivotIndex, low); |
| | |
| | int mid = low + 1; |
| | for (int i = low + 1; i <= high; i++) { |
| | if (numbers[i] < pivot) { |
| | swap(numbers, i, mid); |
| | mid++; |
| | } |
| | } |
| | swap(numbers, low, --mid); |
| | sort(numbers, low, mid - 1); |
| | sort(numbers, mid + 1, high); |
| | return numbers; |
| | } |
| | |
| | public static int[] sort(int[] numbers) { |
| | return sort(numbers, 0, numbers.length - 1); |
| | } |
| | } |