? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
我们在上一篇博客《数值优化:算法分类及收敛性分析基础》介绍了数值优化算法的历史发展、分类及其收敛性/复杂度分析基础。本篇博客我们重点关注一阶确定性优化算法及其收敛性分析。
1 梯度下降法
1.1 算法描述
梯度下降法[1]是最古老的一阶方法,由Cauchy在1847年提出。
梯度下降法的基本思想是:最小化目标函数在当前迭代点处的一阶泰勒展开,从而近似地优化目标函数本身。具体地,对函数f:Rn→Rf:Rn→Rf:\mathbb{R}^n \rightarrow \mathbb{R},将其在第ttt轮迭代点wtwtw^t处求解下述问题:
minwf(w)=minw[f(wt)+∇f(wt)T(w−wt)]minwf(w)=minw[f(wt)+∇f(wt)T(w−wt)]\underset{w}{\text{min}}f(w) = \underset{w}{\text{min}} \left[ f(w^t) + \nabla f(w^t)^T (w-w^t) \right]
上式右端关于自变量www是线性的,并且使得∇f(wt)Tw∇f(wt)Tw\nabla f(w^t)^Tw最小的方向与梯度∇f(wt)∇f(wt)\nabla f(w^t)的方向相反。于是梯度下降法的更新规则如下:
wt+1=wt−η∇f(wt)wt+1=wt−η∇f(wt)w^{t+1} = w^t - \eta \nabla f(w^t)
其中η>0η>0\eta>0是步长,也常被称作学习率。
梯度下降法描述如下:
1.2 收敛性分析
针对不同性质的目标函数,梯度下降法具有不同的收敛速率。由于梯度下降法只适用于梯度存在的函数(没有梯度需要考虑使用次梯度的方法),这里考虑梯度下降法对于光滑凸函数和光滑强凸函数的收敛速率。
光滑凸函数收敛性 假设目标函数f:Rd→Rf:Rd→Rf: \mathbb{R}^d \rightarrow \mathbb{R}是凸函数,且ββ\beta-光滑,当步长η=1βη=1β\eta = \frac{1}{\beta}时,梯度下降法具有O(1t)O(1t)\mathcal{O}(\frac{1}{t})的次线性收敛速率:
f(wt)−f(w∗)⩽2β∥w0−w∗∥2tf(wt)−f(w∗)⩽2β‖w0−w∗‖2tf(w^t) - f(w^) \leqslant \frac{2\beta \lVert w^0 - w^\rVert^2}{t}
光滑强凸函数收敛性 假设目标函数f:Rd→Rf:Rd→Rf: \mathbb{R}^d \rightarrow \mathbb{R}是αα\alpha-强凸函数,且ββ\beta-光滑,当步长η=1βη=1β\eta = \frac{1}{\beta}时,梯度下降法具有O(e−tQ)O(e−tQ)\mathcal{O}(e^{-\frac{t}{Q}})的线性收敛速率:
f(wt)−f(w∗)⩽β2e−tQ∥w0−w∗∥2f(wt)−f(w∗)⩽β2e−tQ‖w0−w∗‖2f(w^t) - f(w^) \leqslant \frac{\beta}{2}e^{-\frac{t}{Q}} \lVert w^0 - w^\rVert^2
其中Q=βαQ=βαQ = \frac{\beta}{\alpha},一般被称为条件数。
通过以上两个定理可知,强凸性质会大大提高梯度下降法的收敛速率。进一步地,强凸性质越好(即αα\alpha越大),条件数QQQ越小,收敛越快。
而光滑性质在凸和强凸两种情形下都会加快梯度下降法的收敛速率,即ββ\beta越小(强凸情景下,条件数QQQ越小),收敛越快。可以说凸情形中的光滑系数和强凸情形中的条件数在一定程度上刻画了优化问题的难易程度。
2 投影次梯度下降法
2.1 算法描述
梯度下降法有两个局限,一是只适用于无约束优化问题,二是只适用于梯度存在的目标函数。投影次梯度法[2]可以解决梯度下降法的这两个局限性。
投影次梯度下降法相比梯度下降法,具有次梯度选择和约束域投影两个特性:
- 次梯度选择 选取当前迭代点wtwtw^t的次梯度集合∂f(wt)∂f(wt)\partial f(w^t)中随机选取一个次梯度gtgtg^t,按照梯度下降更新vt+1=vt−ηgtvt+1=vt−ηgtv^{t+1} = v^t - \eta g^t
得到vt+1vt+1v^{t+1}。 - 约束域投影 确定vt+1vt+1v^{t+1}是否属于约束域WW\mathcal{W},如果属于则直接将其做为wt+1wt+1w^{t+1};如果不属于,则需寻找vt+1vt+1v^{t+1}到约束域WW\mathcal{W}的投影,也就是WW\mathcal{W}中离vt+1vt+1v^{t+1}最近的点。如下图所示:
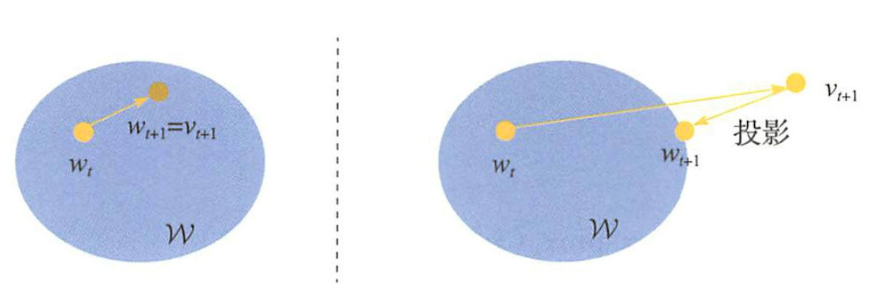
寻找投影的过程可以经由投影映射ΠW( ⋅ )ΠW( ⋅ )\Pi_{\mathcal{W}}(\space \cdot \space)来完成:
wt+1=ΠW(vt+1)=arg minv∈W∥v−vt+1∥wt+1=ΠW(vt+1)=arg minv∈W‖v−vt+1‖\begin{aligned}
w^{t+1} &= \Pi_{\mathcal{W}}(v^{t+1}) \
&= \underset{v\in \mathcal{W}}{\text{arg min}}\lVert v - v^{t+1}\rVert
\end{aligned}
投影次梯度下降法描述如下:
2.2 收敛性分析
在一定步长的选取规则下,投影次梯度法是收敛的,并且收敛速度也依赖于目标函数的凸性和光滑性。
对于ββ\beta-光滑的凸/强凸函数,当步长为1β1β\frac{1}{\beta}时,投影次梯度下降法的收敛率和梯度下降法相同,对于凸函数是O(1t)O(1t)\mathcal{O}(\frac{1}{t}),强凸函数是O(e−tQ)O(e−tQ)\mathcal{O}(e^{-\frac{t}{Q}})。
不过,由于投影次梯度算法适用于有次梯度存在的目标函数,因而不仅适用于光滑函数的优化,也适用于Lipschitz连续函数的优化。对于Lipschitz连续函数,投影次梯度下降法收敛。对于凸函数,步长η=O(1t√)η=O(1t)\eta = \mathcal{O}(\frac{1}{\sqrt{t}})时,收敛速率为O(1t√)O(1t)\mathcal{O}(\frac{1}{\sqrt{t}});对于强凸函数,步长η=O(1t)η=O(1t)\eta = \mathcal{O}(\frac{1}{t})时,收敛速率为O(1t)O(1t)\mathcal{O}(\frac{1}{t})。可以看到其收敛速率在凸和强凸两种情形相比光滑函数显著降低,都是次线性。
3 近端梯度下降法
3.1 算法描述
近端梯度法[3]是投影次梯度法的一种推广,适用于如下形式的部分不可微的凸目标函数的优化问题:
minw∈Wf(w)=l(w)+R(w)minw∈Wf(w)=l(w)+R(w)\underset{w \in \mathcal{W}}{\text{min}} f(w) = l(w) + R(w)
其中l(w)l(w)l(w)是其中的可微凸函数部分,R(w)R(w)R(w)是不可微的凸函数(例如L1L1L_1正则项)。算法的基本思想是先按照可微的lll函数进行一步梯度下降更新:
vt+1=wt−ηt∇l(wt)vt+1=wt−ηt∇l(wt)v^{t+1} = w^t - \eta^t \nabla \mathcal{l}(w^t)
然后再经过近端映射proxR( ⋅ )proxR( ⋅ )\text{prox}_R(\space \cdot \space)做为本轮最终的迭代更新:
wt+1=proxR(vt+1)=arg minv∈W[R(v)+12∥v−vt+1∥2]wt+1=proxR(vt+1)=arg minv∈W[R(v)+12‖v−vt+1‖2]\begin{aligned}
w^{t+1} &= \text{prox}_{R}(v^{t+1}) \
&= \underset{v\in \mathcal{W}}{\text{arg min}}\left[ R(v) + \frac{1}{2}\lVert v - v^{t+1}\rVert^2 \right]
\end{aligned}
近端梯度下降法描述如下:
3.2 收敛性分析
如下定理所示,近端梯度下降法可以达到线性收敛速率。
近端梯度下降法收敛性 假设目标函数中的lll函数是RdRd\mathbb{R}^d上的αα\alpha-强凸函数,且ββ\beta-光滑;RRR函数是RdRd\mathbb{R}^d上的凸函数, 当步长η=1βη=1β\eta = \frac{1}{\beta}时,近端梯度下降法具有O(e−tQ)O(e−tQ)\mathcal{O}(e^{-\frac{t}{Q}})的线性收敛速率:
f(wt)−f(w∗)⩽β2e−tQ∥w0−w∗∥2f(wt)−f(w∗)⩽β2e−tQ‖w0−w∗‖2f(w^t) - f(w^) \leqslant \frac{\beta}{2}e^{-\frac{t}{Q}} \lVert w^0 - w^\rVert^2
其中Q=βαQ=βαQ = \frac{\beta}{\alpha}为lll函数的条件数。
4 Frank-Wolfe算法
4.1 算法描述
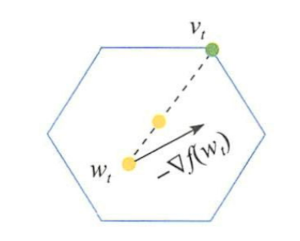
Frank-Wolfe算法[4]是投影次梯度下降法的另一个替代算法。投影次梯度算法虽然适用于有约束优化问题,但是如果投影的计算很复杂,投影次梯度下降的效率将会称为瓶颈。为了解决此问题,不同于投影次梯度下降法中先进行梯度下降再对约束域进行投影的做法,Frank-Wolfe算法在最小化目标函数的泰勒展开时就将约束条件考虑进去,直接得到满足约束的近似最小点,即:
vt=argminv∈W[f(wt)+∇f(wt)T(v−wt)]=argminv∈W∇f(wt)Tvvt=argminv∈W[f(wt)+∇f(wt)T(v−wt)]=argminv∈W∇f(wt)Tv\begin{aligned}
v^t & = \text{argmin}_{v\in\mathcal{W}}\left[ f(w^t) + \nabla f(w^t)^T(v - w^t) \right]\
& = \text{argmin}_{v\in \mathcal{W}} \nabla f(w^t)^Tv
\end{aligned}
为了使算法的解更稳定,Frank-Wolfe算法将求解上述子问题得到的vtvtv^t与当前状态wtwtw^t做线性加权:
wt+1=(1−γt)wt+γtvtwt+1=(1−γt)wt+γtvtw^{t+1} = (1-\gamma^t)w^t + \gamma^tv^t
如下图所示:
Frank-Wolfe算法描述如下:
4.2 收敛性分析
Frank-Wolfe算法收敛速率如下列定理所示:
Frank-Wolfe法收敛性 假设目标函数中的fff函数是RdRd\mathbb{R}^d上的凸函数,且ββ\beta-光滑,当加权系数γt=2t+1γt=2t+1\gamma^t = \frac{2}{t+1}时,Frank-Wolfe算法具有O(1t)O(1t)\mathcal{O}(\frac{1}{t})的次线性收敛速率:
f(wt)−f(w∗)⩽2βD2tf(wt)−f(w∗)⩽2βD2tf(w^t) - f(w^*) \leqslant \frac{2\beta D^2}{t}
其中D=supw,v∈W∥w−v∥D=supw,v∈W‖w−v‖D = \underset{w, v \in \mathcal{W}}{\text{sup}}\lVert w - v \rVert。
由于Frank-Wolfe算法的收敛速率和投影次梯度下降法相同,可以依据要解决问题中的投影计算是否困难,在两种算法中选择一种使用。
5 Nesterov加速法
5.1 算法描述
考虑以上所有的一阶算法。在Lipschitz连续的条件下,梯度下降法达到了一阶算法的收敛速率下界。然而对于光滑函数,一阶方法的收敛速率的下界小于梯度下降法的收敛速率。一阶方法在凸情形下的收敛率下界为O(1t2)O(1t2)\mathcal{O}(\frac{1}{t^2}),强凸情形下的下界为O(e−tQ√)O(e−tQ)\mathcal{O}(e^{-\frac{t}{\sqrt{Q}}});而梯度下降法在凸情形下的收敛率为O(1t)O(1t)\mathcal{O}(\frac{1}{t}),强凸情形下的收敛率为O(e−tQ)O(e−tQ)\mathcal{O}(e^{-\frac{t}{Q}})。这说明我们可以针对光滑函数设计收敛速率更快的一阶方法。
Nesterov在1983年对光滑度目标函数提出了加快一阶优化算法收敛的方法[5]。我们这里以梯度下降法为例,介绍Nesterov加速法的具体实现。
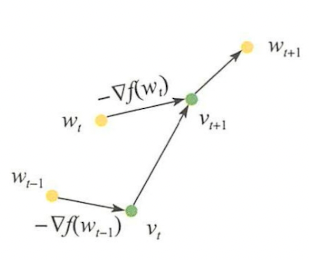
Nesterov算法的基本原理如下图所示:
当任意时刻ttt,对当前状态wtwtw^t进行一步梯度迭代得到辅助变量vt+1vt+1v^{t+1}:
vt+1=wt−ηt∇f(wt)wt+1vt+1=wt−ηt∇f(wt)wt+1v^{t+1} = w^t - \eta^t \nabla f(w^t)
w^{t+1}
然后将新的辅助变量和上一轮迭代计算的辅助变量vtvtv^t做线性加权,做为第t+1t+1t+1轮迭代的参数wt+1wt+1w^{t+1}。对于凸和强凸的目标函数,线性加权系数有所不同。
具体地,对于强凸的目标函数,加权规则如下:
wt+1=(1+γt)vt+1−γtvtwt+1=(1+γt)vt+1−γtvtw^{t+1} = (1 + \gamma^t)v^{t+1} - \gamma^t v^t
其中γt=1−Q√1+Q√γt=1−Q1+Q\gamma^t = \frac{1-\sqrt{Q}}{1 + \sqrt{Q}},QQQ为条件数。
对于凸的目标函数,加权规则如下:
wt+1=(1−γt)vt+1+γtvtwt+1=(1−γt)vt+1+γtvtw^{t+1} = (1 - \gamma^t)v^{t+1} + \gamma^t v^t
其中γt=1−λtλt+1γt=1−λtλt+1\gamma^t = \frac{1 - \lambda^t}{\lambda^{t+1}},λ0=0λ0=0\lambda^0 = 0, λt=1+1+4(λt−1)2√2λt=1+1+4(λt−1)22\lambda^t = \frac{1 + \sqrt{1 + 4{(\lambda^{t-1})}^2}}{2}。
Nesterov加速算法描述如下:
5.2 收敛性分析
Nesterov证明了用以上方法加速之后的梯度下降法的收敛速率可以达到针对光滑目标函数的一阶方法的收敛速率下界:
光滑凸函数收敛性 假设目标函数f:Rd→Rf:Rd→Rf: \mathbb{R}^d \rightarrow \mathbb{R}是凸函数,并且ββ\beta-光滑,当步长η=1βη=1β\eta = \frac{1}{\beta}时,Nesterov加速法能够将收敛速率提高到O(1t2)O(1t2)\mathcal{O}({\frac{1}{t^2}})(不过仍是次线性收敛速率):
f(wt)−f(w∗)⩽2β∥w0−w∗∥2t2f(wt)−f(w∗)⩽2β‖w0−w∗‖2t2f(w^t) - f(w^) \leqslant \frac{2\beta \lVert w^0 - w^\rVert^2}{t^2}
光滑强凸函数收敛性 假设目标函数f:Rd→Rf:Rd→Rf: \mathbb{R}^d \rightarrow \mathbb{R}是αα\alpha-强凸函数,并且ββ\beta-光滑,当步长η=1βη=1β\eta = \frac{1}{\beta}时,Nesterov加速法能够将收敛速率提高到e−tQ√e−tQ\mathcal{e^{-\frac{t}{\sqrt{Q}}}}(不过仍是线性收敛速率):
f(wt)−f(w∗)⩽α+β2e−tQ√∥w0−w∗∥2f(wt)−f(w∗)⩽α+β2e−tQ‖w0−w∗‖2f(w^t) - f(w^) \leqslant \frac{\alpha + \beta}{2}e^{-\frac{t}{\sqrt{Q}}} \lVert w^0 - w^\rVert^2
其中Q=βαQ=βαQ = \frac{\beta}{\alpha}为条件数。
6 坐标下降法
6.1 算法描述
坐标下降法[6]是另外一种常见的最小化实值函数的方法。其基本思想是,在迭代的每一步,算法选择一个维度,并更新这一维度,其它维度的参数保持不变;或者将维度分为多个块,每次只更新某块中的维度,其它维度保持不变。坐标下降法的更新公式如下:
wt+1j=arg minz∈Wjf(wt1,...,wtj−1,z,wtj+1,...,wtd)wjt+1=arg minz∈Wjf(w1t,...,wj−1t,z,wj+1t,...,wdt)w^{t+1}_j = \underset{z\in \mathcal{W}_j}{\text{arg min}}f(w^t_1,...,w^t_{j-1}, z, w^t_{j+1},...,w^t_d)
其中,WjWj\mathcal{W}_j为第jjj个维度块的约束域。
对于维度的选择,坐标下降法一般遵循以下本征循环选择规则(Essential Cyclic Rule):存在一个常数r⩾dr⩾dr\geqslant d,使得对任意的sss,对于每一个维度jjj,在第sss轮和第s+r−1s+r−1s + r - 1轮之间都至少选择一次。最常见的方法是循环选择规则,即对于任意j=1,...,dj=1,...,dj=1,...,d,分别在第j,d+j,2d+j,...j,d+j,2d+j,...j, d + j, 2d + j,...次算法迭代中选择维度jjj(即每隔ddd轮选择一次)。
6.2 收敛性分析
可以证明对于强凸并且光滑的目标函数,循环坐标下降法具有线性的收敛速率[6]。
参考
- [1] Cauchy A. Méthode générale pour la résolution des systemes d’équations simultanées[J]. Comp. Rend. Sci. Paris, 1847, 25(1847): 536-538.
- [2]
Levitin E S, Polyak B T. Constrained minimization methods[J]. USSR Computational mathematics and mathematical physics, 1966, 6(5): 1-50. - [3] Parikh N, Boyd S. Proximal algorithms[J]. Foundations and Trends in optimization, 2014, 1(3): 127-239.
- [4] Frank M, Wolfe P. An algorithm for quadratic programming[J]. Naval research logistics quarterly, 1956, 3(1‐2): 95-110.
- [5] Nesterov Y E. A method for solving the convex programming problem with convergence rate O (1/k^ 2)[C]//Dokl. akad. nauk Sssr. 1983, 269: 543-547.
-
[6]
Wright S J. Coordinate descent algorithms[J]. Mathematical Programming, 2015, 151(1): 3-34. - 1.1 算法描述
- 1.2 收敛性分析
- 2 投影次梯度下降法
- 2.1 算法描述
- 2.2 收敛性分析
- 3 近端梯度下降法
- 3.1 算法描述
- 3.2 收敛性分析
- 4 Frank-Wolfe算法
- 4.1 算法描述
- 4.2 收敛性分析
- 5 Nesterov加速法
- 5.1 算法描述
- 5.2 收敛性分析
- 6 坐标下降法
- 6.1 算法描述
- 6.2 收敛性分析
-
__EOF__
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wd9NuL9B-1655009379066)(https://blog.csdn.net/orion-orion)]猎户座 - 本文链接: https://blog.csdn.net/orion-orion/p/16367015.html
- 关于博主: 本科CS系蒟蒻,机器学习半吊子,并行计算混子。
- 版权声明: 欢迎您对我的文章进行转载,但请务必保留原始出处哦(^▽^)。
- 声援博主: 如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。
转载请注明:xuhss » 数值优化:经典一阶确定性算法及其收敛性分析