? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
神经网络的原理
对于一个神经网络我们可以分为输入层,隐藏层,输出层,对于神经网络的训练可以分为正向传播和反向传播。这里对神经网络不同层次的数据表示进行约定。这里我们以一个二层的神经网络模型进行演示。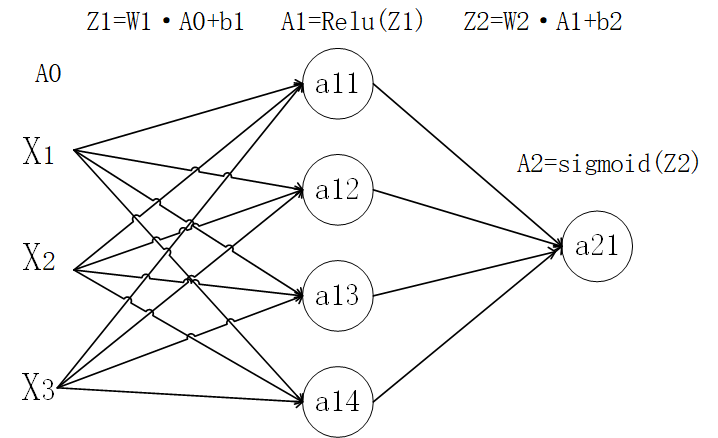
在这里我们将A0定义为输入层数据,将A1定义为隐藏层数据,最后的A2定义为输出层数据。这A0时输入的矩阵通常为(m,n)m为特征个数,n为样本个数。对于L层,AL层为a个元素,L-1层有b
个,这里我们就可以直到WL为形状(a,b)的矩阵,bL为(1,b)的矩阵,输入的AL-1为(b,n)的矩阵,得到ZL和AL为(a,n)的矩阵。
向前传播
向前传播比较简单,主要就是和上面图片一样,每一层可以看作一个单独的逻辑回归,只不过一层的激活函数可能不同,通常使用的是Relu或者tanh函数作为激活函数。
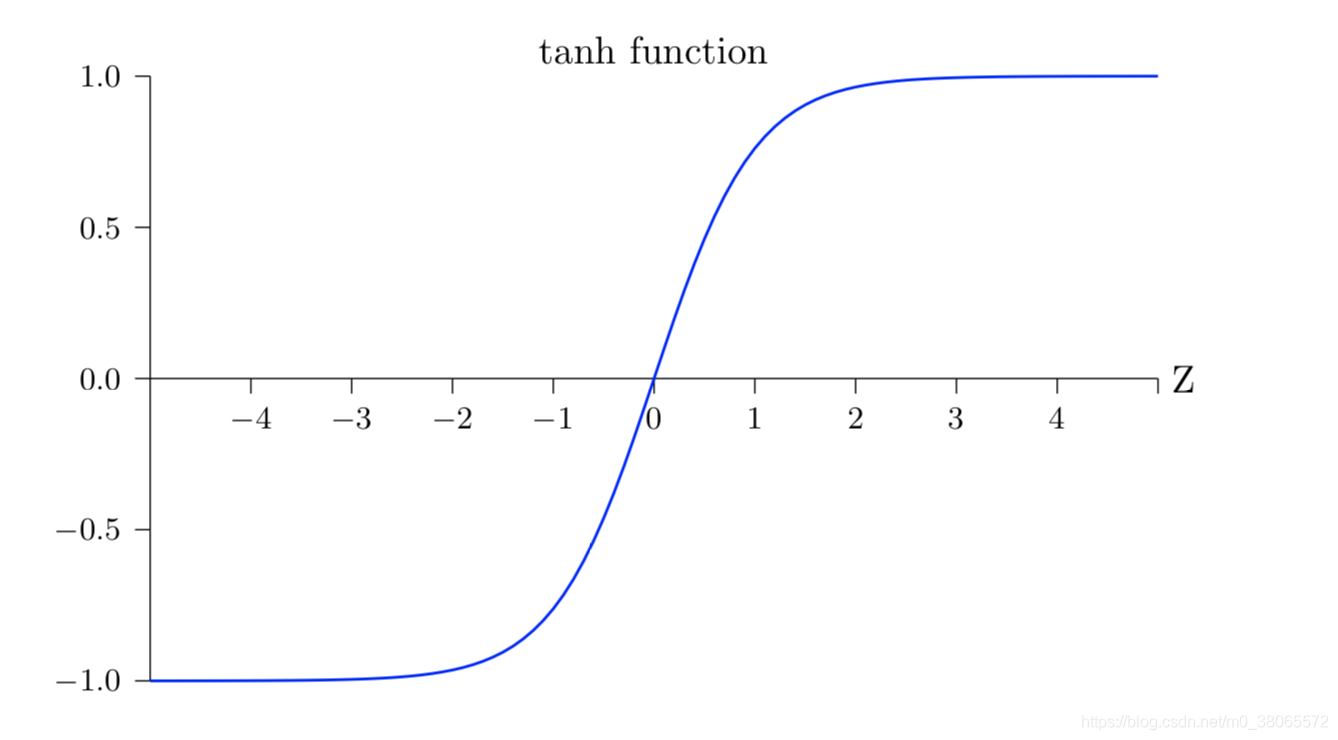
具体的计算过程如下:
Z[i]=W[i]A[i−1]+b[i]A[i]=σ(Z[i])Z[i+1]=W[i+1]A[i]+b[i+1]A[i+1]=σ(Z[i+!])## 反向传播
反向传播的本质是依据链式发展对每一层都求出w和b的偏导数,只用进行一个变量修改,实现对代价函数的一个求极值过程。假设该神经网络有L层,最后一层的激活函数为:
A[L]=sigmod(z)=11+e−z对于代价函数可以求得为:
J(W,b)=−1m∑1m[yilog(ALi)+(1−y)log(1−ALi)]所以对于最后一层我们可以计算得到:
dJdAL=−1m[YAL−−1−Y1−AL]这里计算的是矩阵除法,得到的对应的一个矩阵。
之后计算关于的一个方向倒数,假设激活函数为σ(z)
是激活函数点的导数值dJdZL=dJdALσ‘(σ‘是激活函数z点的导数值)已知已知ZL=WLA[L−1]+b所以可以依据链式法则求出dJdWL和dJdbL:
dJdWL=dJdZL·dZLdWL=dJdZL·AL−1dJdbL=dJdZL依据链式法则还可以求出:
dJdAL−1=dJdZL·WL之后进行循环,获取每一层对应的w和b的梯度,用于进行一个数据的更新。
对于反向传播的具体流程大致就是上面公式所示,具体可以能符号有些错误但思想是这样的。
转载请注明:xuhss » 深度学习-神经网络原理2