? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
本章是系列文章的第三章,介绍了基于数据流分析的一些优化方法。包括生命周期管理,可获得表达式,常用表达式,可达性定义。本章在介绍这4中分析方法的基础上提取出它们的通用模式。这一章形式化的内容比较多,看的时候有点烧脑,最好自己手工推导一下,要不然基本上看不懂:)
本文中的所有内容来自学习DCC888的学习笔记或者自己理解的整理,如需转载请注明出处。周荣华@燧原科技
3.1 生命周期
对下面的程序:
1 var x,y,z;
2 x = input;
3 while (x > 1) {
4 y = x / 2;
5 if (y > 3)
6 x = x - y;
7 z = x - 4;
8 if (z > 0)
9 x = x / 2;
10 z = z - 1;
11 }
12 output x;可以生成控制流图如下:

图对应dot文件内容:
1 digraph "CFG for 3.1"{
2 rankdir=LR
3 "var x,y,z" -> "x = input" -> "x > 1" -> {"output x" "y = x / 2"}
4 "y = x / 2" -> "y > 3" -> {"x = x - y" "z = x - 4"}
5 "x = x - y" -> "z = x - 4" -> "z > 0" -> {"x = x / 2" "z = z - 1"}
6 "x = x / 2" -> "z = z - 1" -> "x > 1"但仅有控制流分析,还有很多问题无法解决。第一个问题是计算机需要知道这个程序需要多少寄存器,甚至需要控制流执行到某条边的时候,需要多少个寄存器?有什么通用的方法能用来回答这个问题?
活跃变量:如果程序在执行点需要使用某个变量,并且该使用不是定义类的使用,那么程序需要在紧靠该执行点之前就要能访问这个变量,这种变量称为活跃变量(alive)。
对每个程序执行点p,我们定义2个集合:
- IN是在紧靠p之前活着的变量集合。
- OUT是在紧靠p之后或者的变量集合。
活跃变量的数据流等式:
对 p : v = E
IN(p) = ( OUT(p) \ {v} ) ∪ vars(E)
OUT(p) = ∪ IN(ps), ps ∈ succ(p)
IN(p):p之前的活跃的变量集合
OUT(p):p之后的活跃的变量集合
vars(E):表达式E中出现的所有变量的集合
succ(p):控制流图中p的所有后继的集合
对CFG上的每个点,变量上面2个等式,直到2个集合不再变化,我们就得到了任意点的变量生命周期。
这个等式最早是Albeit用prolog实现的:
1 diff([], \_, []).
2 diff([H|T], L, LL) :- member(H, L), diff(T, L, LL).
3 diff([H|T], L, [H|LL])
4 :- \+member(H, L), diff(T, L, LL).
5 union([], L, L).
6 union([H|T], L, LL) :- member(H, L), union(T, L, LL).
7 union([H|T], L, [H|LL])
8 :- \+ member(H, L), union(T, L, LL).
9 in(1, L) :- out(1, Out), diff(Out, [y], L).
10 in(2, L) :- out(2, Out), diff(Out, [x], L).
11 in(3, L) :- out(3, Out), diff(Out, [z], Diff),
12 union(Diff, [x, y], L).
13 in(4, L) :- out(4, Out), union(Out, [z], L).
14 out(1, L) :- in(2, L).
15 out(2, L) :- in(3, L).
16 out(3, L) :- in(4, L).
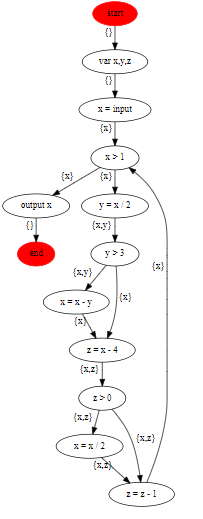
17 out(4, []).上面的控制流图,给每条边加上变量的生命周期之后的结果的dot表达是这样的:
1 digraph "CFG for 3.2"{
2 "start" [bgcolor=black color=red style=filled]
3 "start" -> "var x,y,z" [xlabel="{}"]
4 "var x,y,z" -> "x = input" [xlabel="{}"]
5 "x = input" -> "x > 1" [xlabel="{x}"]
6 "x > 1" -> "output x" [xlabel="{x}"]
7 "x > 1" -> "y = x / 2" [xlabel="{x}"]
8 "y = x / 2" -> "y > 3" [xlabel="{x,y}"]
9 "y > 3" -> "x = x - y" [xlabel="{x,y}"]
10 "y > 3" -> "z = x - 4" [xlabel="{x}"]
11 "x = x - y" -> "z = x - 4" [xlabel="{x}"]
12 "z = x - 4" -> "z > 0" [xlabel="{x,z}"]
13 "z > 0" -> "x = x / 2" [xlabel="{x,z}"]
14 "z > 0" -> "z = z - 1" [xlabel="{x,z}"]
15 "x = x / 2" -> "z = z - 1" [xlabel="{x,z}"]
16 "z = z - 1" -> "x > 1" [xlabel="{x}"]
17 "output x" -> "end" [xlabel="{}"]
18 "end" [bgcolor=black color=red style=filled]
19 }dot文件生成的svg图是这样的:
3.2 可访问表达式(Available Expressions)
可访问表达式:一个表达式E在程序点p是可访问表达式,当且仅当:
-
- E在p之前是可访问表达式,
- 并且E的任意一个变量在p未重新定义;
或者:
-
- E在p处被使用,
- E的所有变量没有在p处重新定义。
可访问表达式的数据流等式:
对 p : v = E
IN(p) = ∩OUT(ps), ps ∈ pred(p)**
OUT(p) = ( IN(p) ∪ {E}) \ {Expr(v)}**
IN(p):p之前的可访问表达式集合
OUT(p):p之后的可访问表达式集合pred(p):控制流图中p的所有前驱的集合
Expr(v):使用变量v的所有表达式的集合
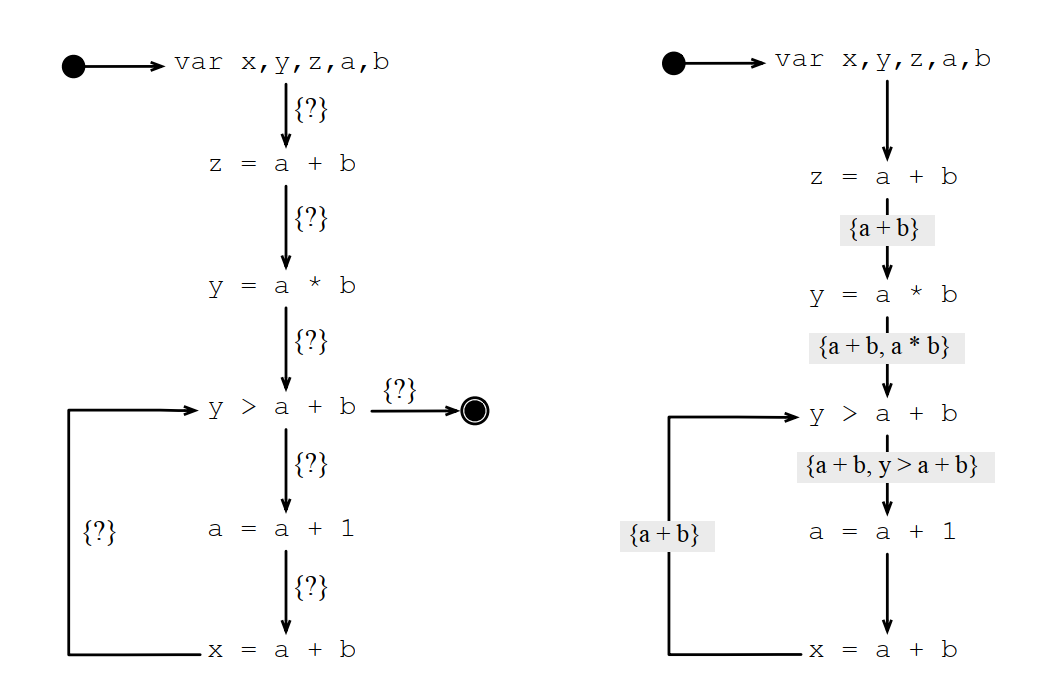
可访问表达式的例子:
3.3 常用表达式(Very Busy Expressions)
常用表达式:当表达式E从p开始到程序结束前的每条路径上都会计算,则称表达式E在p处是常用表达式。形式化描述就是:
-
- E在p之后是常用表达式,
- 并且E的所有变量并没有在p处重新定义;
或者:
-
- p处使用了表达式E。
**常用表达式的数据流等式:**
对 p : v = E
IN(p) = ( OUT(p) \ {Expr(v)}) ∪ {E}
OUT(p) = ∩ IN(ps), ps ∈ succ(p)
IN(p):p之前的常用表达式集合
OUT(p):p之后的常用表达式集合
succ(p):控制流图中p的所有后继的集合
常用表达式的例子:
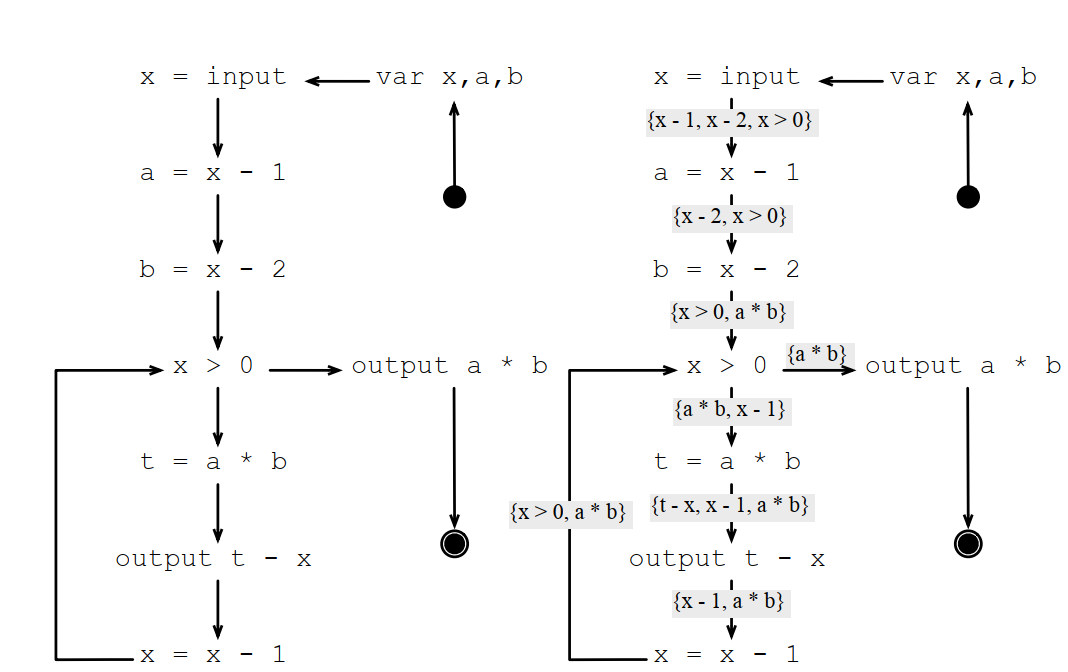
安全的代码修改(Safe Code Hositing):如果某个修改,在任何场景下都不会导致程序做额外的工作,该修改就是安全的修改。
3.4 可获得性定义(Reaching Definitions)
可获得性定义:如果控制流图上存在一条边从程序点p到程序点p‘,并且这条边上没有任意一个结点对变量v重新定义,则称为p在程序点p定义的变量v在程序的p'可获得。
可获得性的推导:变量v在程序点p可获得当且仅当:
-
- 在p之前v可获得,
- 并且v在p处没有重新定义;
或者
-
- p处定义了变量v。
可获得性定义的数据流等式:
对 p : v = E
IN(p) = ∪ OUT(ps), ps ∈ pred(p)**
OUT(p) = ( IN(p) \ {defs(v)} )∪ {(p, v)}**
IN(p):p之前的可获得性定义集合
OUT(p):p之后的可获得性定义集合defs(v):程序中所有v的定义集合
(p, v): p处定义的v
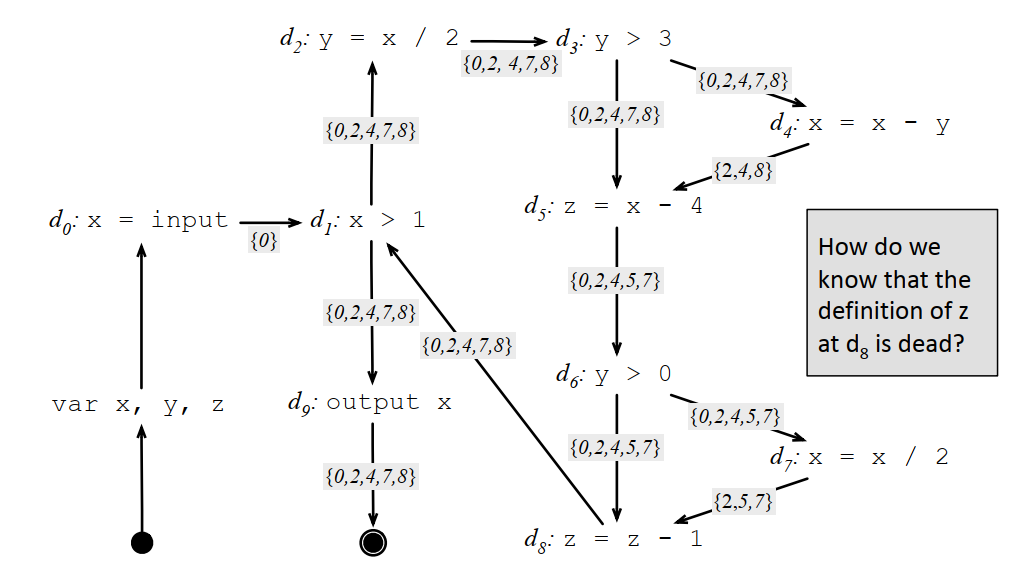
可获得性定义的例子:
3.5 MONOTONE框架
3.5.1 几种数据流分析方法的比较
本章学到了四种数据流分析方法:

数据流分析按汇总方向有正向分析和反向分析两种。
正向分析是从程序的起始点往结束点方向分析,每次输入都是通过这之前所有的输出通过运算(交集或者并集)得到,输出是基于p点的输入和p点的表达式计算出来。例如本章讲到的可获得性定义和可访问表达式的分析。
反向分析相反,需要从程序的结束点往起始点分析,分析方向和数据流动的方向相反。每次先计算输出,每个p的输出都是这之后的输入通过运算得到,输入是基于p点的输出和p点的表达式计算出来。例如本章讲到的生命周期分析和常用表达式分析。
按汇总方法有可以分为确定性分析(MUST,必须)和可能性分析(MAY,可以)2种。区别在于集合从多点汇聚到一个点的时候应该使用交集还是并集。
3.5.2 转换函数
数据流分析过程需要对程序进行一些翻译,数据流分析不能直接分析程序的具体语义(要不然就永远分析不完了),而是分析一种抽象的语义。转换函数就是抽取程序的抽象语义的函数。
正向分析的转换函数是通过输入生成输出的函数:
OUT[s] = fs(IN[s])
相反,反向分析的转换函数是通过输出计算输入的函数:
IN[s] = fs(OUT[s])
3.5.3 合并函数
合并函数确定多条岔路汇聚成一条路或者一条路分成多条岔路时的处理过程。
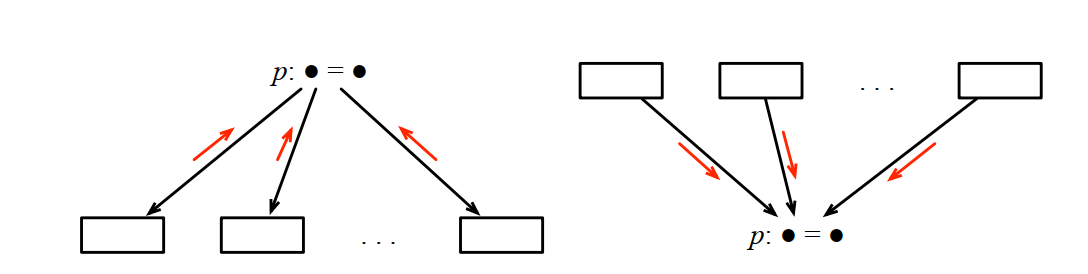
给定一个转换函数,一个合并函数,和一个特定的初始化的IN和OUT的集合,能够证明它必然导致抽象翻译的正常结束。
数据流分析的过程就是按上面的框架找到一个转换函数,和一个合并函数,并给定一个IN和OUT的初始集合。
3.5.4 数据流分析简史
- Frances Allen got the Turing Award of 2007. Some of her contributions touch dataflow analyses.
- Allen, F. E., "Program Optimizations", Annual Review in Automatic Programming 5 (1969), pp. 239-307
- Allen, F. E., "Control Flow Analysis", ACM Sigplan Notices 5:7 (1970), pp. 1-19
- Kam, J. B. and J. D. Ullman, "Monotone Data Flow Analysis Frameworks", Actal Informatica 7:3 (1977), pp. 305-318
- Kildall, G. "A Unified Approach to Global Program Optimizations", ACM Symposium on Principles of Programming Languages (1973), pp. 194-206
转载请注明:xuhss » 程序分析与优化 – 3 数据流分析