? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
本章是系列文章的第五章,介绍了指针分析方法。指针分析在C/C++语言中非常重要,分析的结果可以有效提升指针的优化效率。
本文中的所有内容来自学习DCC888的学习笔记或者自己理解的整理,如需转载请注明出处。周荣华@燧原科技
5.1 概念
- 指针是许多重要编程语言的特性之一
- 指针的使用,可以避免大量的数据拷贝
- 指针的分析的难度很大,并且一直是理解和修改程序的主要障碍
- 指针分析(Pointer Analysis),又可以称为别名分析(Alias Analysis),或者指向分析(Points-To Analysis)
5.2 为什么需要指针分析
1 #include
2 int main() {
3 int i = 7;
4 int *p = &i;
5 *p = 13;
6 printf("The value of i = %d\n", i);
7 }给定上面的例子。gcc的-O1选项能优化成什么样子?
将上述代码保存到pta5.1.cc,并使用“gcc -O1 pta5.1.cc -S”进行编译,生成的汇编代码如下:
1 .file "pta5.1.cc"
2 .section .rodata.str1.1,"aMS",@progbits,1
3 .LC0:
4 .string "The value of i = %d\n"
5 .text
6 .globl main
7 .type main, @function
8 main:
9 .LFB30:
10 .cfi\_startproc
11 subq $8, %rsp
12 .cfi\_def\_cfa\_offset 16
13 movl $13, %edx
14 movl $.LC0, %esi
15 movl $1, %edi
16 movl $0, %eax
17 call \_\_printf\_chk
18 movl $0, %eax
19 addq $8, %rsp
20 .cfi\_def\_cfa\_offset 8
21 ret
22 .cfi\_endproc
23 .LFE30:
24 .size main, .-main
25 .ident "GCC: (Ubuntu 5.4.0-6ubuntu1~16.04.12) 5.4.0 20160609"
26 .section .note.GNU-stack,"",@progbits从汇编代码看,程序直接忽略掉了第3行和第4行的初始化和传地址操作,直接实现了第5行的赋值和第6行的打印。性能是不是强大了很多。
再看个例子:
1 #include
2 #include
3 void sum0(int *a, int *b, int *r, int N) {
4 int i;
5 for (i = 0; i < N; i++) {
6 r[i] = a[i];
7 if (!b[i]) {
8 r[i] = b[i];
9 }
10 }
11 }
12 void sum1(int *a, int *b, int *r, int N) {
13 int i;
14 for (i = 0; i < N; i++) {
15 int tmp = a[i];
16 if (!b[i]) {
17 tmp = b[i];
18 }
19 r[i] = tmp;
20 }
21 }
22 void print(int *a, int N) {
23 int i;
24 for (i = 0; i < N; i++) {
25 if (i % 10 == 0) {
26 printf("\n");
27 }
28 printf("%8d", a[i]);
29 }
30 }
31 #define SIZE 10000
32 #define LOOP 100000
33 int main(int argc, char **argv) {
34 int *a = (int *)malloc(SIZE * 4);
35 int *b = (int *)malloc(SIZE * 4);
36 int *c = (int *)malloc(SIZE * 4);
37 int i;
38 for (i = 0; i < SIZE; i++) {
39 a[i] = i;
40 b[i] = i % 2;
41 }
42 if (argc % 2) {
43 printf("sum0\n");
44 for (i = 0; i < LOOP; i++) {
45 sum0(a, b, c, SIZE);
46 }
47 } else {
48 printf("sum1\n");
49 for (i = 0; i < LOOP; i++) {
50 sum1(a, b, c, SIZE);
51 }
52 }
53 }在教材中提供的编译器编译的结果看,-O1无法有效优化sum0的指针操作,但对sum1手工优化后的代码能很好的进行指针优化。这是教材中提供的运行数据:
1 $> time ./a.out
2 sum0
3 0 1 0 3
4 0 11 0 13
5 real 0m6.299s
6 user 0m6.285s
7 sys 0m0.008s
8 $> time ./a.out a
9 sum1
10 0 1 0 3
11 0 11 0 13
12 real 0m1.345s
13 user 0m1.340s
14 sys 0m0.004s但我用gcc5编译实测下来的结果是-O0,确实不会优化,-O1仍然有很好的优化(时间是-O0的十分之一),并且sum0和sum1性能上差别不大,说明编译器进化的非常快。
1 ronghua.zhou@794bb5fbd58a:~/DCC888$ gcc pta5.2.c -O0
2 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out
3 sum0
4
5 real 0m5.772s
6 user 0m5.767s
7 sys 0m0.004s
8 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out a
9 sum1
10
11 real 0m4.766s
12 user 0m4.761s
13 sys 0m0.004s
14 ronghua.zhou@794bb5fbd58a:~/DCC888$ gcc pta5.2.c -O1
15 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out
16 sum0
17
18 real 0m0.542s
19 user 0m0.541s
20 sys 0m0.000s
21 ronghua.zhou@794bb5fbd58a:~/DCC888$ time ./a.out a
22 sum1
23
24 real 0m0.473s
25 user 0m0.473s
26 sys 0m0.000s由于sum0和sum1本身计算时间相差不大,所以外面主要对比一下sum0在-O0时的代码和-O1时的代码的差别。
不优化的结果:
1 sum0:
2 .LFB2:
3 .cfi\_startproc
4 pushq %rbp
5 .cfi\_def\_cfa\_offset 16
6 .cfi\_offset 6, -16
7 movq %rsp, %rbp
8 .cfi\_def\_cfa\_register 6
9 movq %rdi, -24(%rbp)
10 movq %rsi, -32(%rbp)
11 movq %rdx, -40(%rbp)
12 movl %ecx, -44(%rbp)
13 movl $0, -4(%rbp)
14 jmp .L2
15 .L4:
16 movl -4(%rbp), %eax
17 cltq
18 leaq 0(,%rax,4), %rdx
19 movq -40(%rbp), %rax
20 addq %rax, %rdx
21 movl -4(%rbp), %eax
22 cltq
23 leaq 0(,%rax,4), %rcx
24 movq -24(%rbp), %rax
25 addq %rcx, %rax
26 movl (%rax), %eax
27 movl %eax, (%rdx)
28 movl -4(%rbp), %eax
29 cltq
30 leaq 0(,%rax,4), %rdx
31 movq -32(%rbp), %rax
32 addq %rdx, %rax
33 movl (%rax), %eax
34 testl %eax, %eax
35 jne .L3
36 movl -4(%rbp), %eax
37 cltq
38 leaq 0(,%rax,4), %rdx
39 movq -40(%rbp), %rax
40 addq %rax, %rdx
41 movl -4(%rbp), %eax
42 cltq
43 leaq 0(,%rax,4), %rcx
44 movq -32(%rbp), %rax
45 addq %rcx, %rax
46 movl (%rax), %eax
47 movl %eax, (%rdx)
48 .L3:
49 addl $1, -4(%rbp)
50 .L2:
51 movl -4(%rbp), %eax
52 cmpl -44(%rbp), %eax
53 jl .L4
54 nop
55 popq %rbp
56 .cfi\_def\_cfa 7, 8
57 ret
58 .cfi\_endproc
59 .LFE2:
60 .size sum0, .-sum0
61 .globl sum1
62 .type sum1, @functionO1优化后的结果:
1 sum0:
2 .LFB38:
3 .cfi\_startproc
4 testl %ecx, %ecx
5 jle .L1
6 movl $0, %eax
7 .L4:
8 movl (%rdi,%rax,4), %r9d
9 movl %r9d, (%rdx,%rax,4)
10 movl (%rsi,%rax,4), %r8d
11 testl %r8d, %r8d
12 cmovne %r9d, %r8d
13 movl %r8d, (%rdx,%rax,4)
14 addq $1, %rax
15 cmpl %eax, %ecx
16 jg .L4
17 .L1:
18 rep ret
19 .cfi\_endproc
20 .LFE38:
21 .size sum0, .-sum0
22 .globl sum1
23 .type sum1, @function这个函数从O0到O1的优化过程中使用了很多优化方法,对于这里说的指针分析,由于指针的求地址和解引用非常耗时,O1使用cmovne将必要和拷贝优化成单个指令,起到了很好的效果。
在大多数情况下,sum0和sum1是等价的,但如果b和r这2个指针指向同一个地址的时候,2个算法就会有一些差别,所以编译器不能直接将sum0优化成sum1。
5.3 指针分析
指针分析的目标是找到每个指针指向的地址。
指针分析经常使用基于约束系统的分析方法来描述和解决。
性能最好的指针分析算法的复杂度是O(n3)。
为了提升效率和精准度,指针分析是编译器设计中仅次于寄存器分配方法的第二大课题。
5.4 尝试使用数据流分析方法解决指针分析
如下图所示,由于l2和l5会相互影响,但很难通过简单的语法分析就能找到他们之间的联系,所以基本的数据流分析对指针分析会失效。
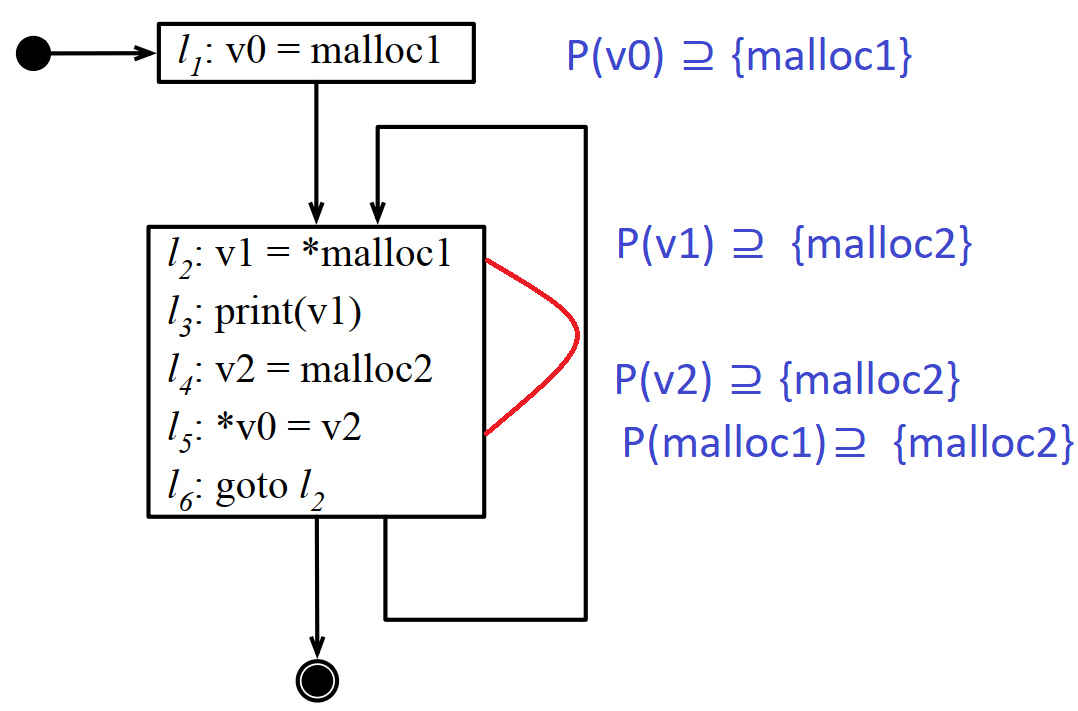
5.5 ANDERSEN指针分析算法
常见的四种指针构造过程(控制流分析里面原来用⊆表达右边是左边的约束,但这个很容易和之前求指针分析时的约束弄混,因为约束是⊇,换算成控制流要转向成⊆,不知道别人会不会晕,反正我被弄晕了。所以最后我改成<-表示控制流图里面的边的方向,这样看着稍微好懂点):
| 指令 | 约束名 | 约束 | 控制流分析结果 |
|---|---|---|---|
| a = &b | base | P(a)⊇ {b} | lhs <- rhs |
| a = b | simple | P(a)⊇ P(b) | lhs <- rhs |
| a = *b | load | t ∈ P(b)⇒ P(a)⊇ P(t) | {t} <- rhs' ⇒ lhs <- rhs |
| *a = b | store | t ∈ P(a)⇒ P(t)⊇ P(b) | {t} <- rhs' ⇒ lhs <- rhs |
Andersen指针分析法,又称为基于集合包含的的约束分析法。Anderson的指向图算法:
1 let G = (V, E)
2 W = V
3 while W ≠ [] do
4 n = hd(W)
5 for each v ∈ P(n) do
6 for each load "a = *n" do
7 if (v, a) ∉ E then
8 E = E ∪ {(v, a)}
9 W = v::W
10 for each store "*n = b" do
11 if (b, v) ∉ E then
12 E = E ∪ {(v, a)}
13 W = b::W
14 for each (n, z) ∈ E do
15 P(z) = P(z) ∪ P(n)
16 if P(z) has changed then
17 W = z::W上面的算法做一些解释:
W = v::W 的含义是将W这个数组的头部增加一个元素v。
n = hd(W) 表示从数组W中取出头结点,赋值给n。
例如,对下面的代码:
1 b = &a
2 a = &c
3 d = a
4 *d = b
5 a = *d生成的指向图是这样的:
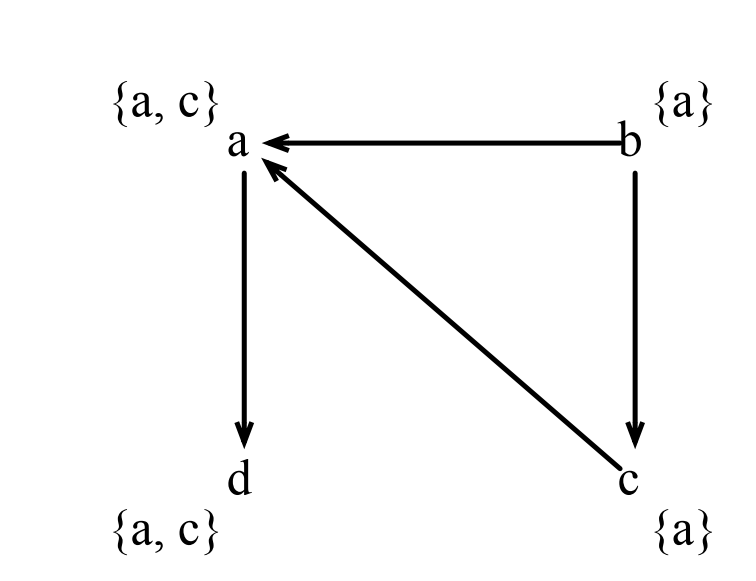
5.6 循环坍塌(COLLAPSING CYCLES)
找到图的传递闭包的算法复杂度达到O(n3),使得科学家们一直没停止过对它的优化。
循环坍塌是二十一世纪出发现的一种优化方法,循环坍塌的理论基础是强连通图的拓扑一致性,在指向分析图中,表示形成循环的所有节点,都有一致的指向分析集合。
算法能用和算法在实际中能用是两个概念。
5.6.1 循环识别
DFS可以发现循环,但发现的复杂度也不低。DFS的目标是遍历所有节点,但如果想要通过DFS发现环的话,就不但要记录节点,还要记录节点的所有边,这样才能区别一个节点的子结点已经遍历过的情况下判断出只是菱形依赖,还是环。
常见的循环识别方法有波传递算法(Wave propagation),深度传递算法(Deep propagation)和惰性循环检测方法(Lazy cycle detection)。
5.6.2 惰性循环检测(Lazy Cycle Detection)
参见The ant and the grasshopper: fast and accurate pointer analysis for millions of lines of code, 2007。这篇文章实际提出了两种循环检测方法,一种是惰性循环检测,一种是混合循环检测。
增加惰性循环检测之后的算法相对于没有循环检测的方法,主要增加了第2行和第16~18行。其中第2行是增加了一个集合初始化(用来避免重复进行循环检测)。16~18行主要是发现某条边的2个节点的指向集合相等的情况下触发循环检测,检测成功就直接触发循环坍塌。不论是否检测到循环,都会将疑似循环的边加入到已检测的集合中。
1 let G = (V, E)
2 R = {}
3 W = V
4 while W ≠ [] do
5 n = hd(W)
6 for each v ∈ P(n) do
7 for each load "a = *n" do
8 if (v, a) ∉ E then
9 E = E ∪ {(v, a)}
10 W = v::W
11 for each store "*n = b" do
12 if (b, v) ∉ E then
13 E = E ∪ {(v, a)}
14 W = b::W
15 for each (n, z) ∈ E do
16 if P(z) = P(n) and (n, z) ∉ R then
17 DETECTANDCOLLAPSECYCLES(z)
18 R = R∪ {(n, z)}
19 P(z) = P(z) ∪ P(n)
20 if P(z) has changed then
21 W = z::W优点:仅在非常大可能性能找到环的情况下才触发环形检测;概念简单,容易实现。
缺点:触发检测前环已经存在一段时间,会降低部分性能;即使概率很大的时候,环形检测还是有可能失败(当前还没有失败的证据)。
对下面的伪代码:
1 c = &d
2 e = &a
3 a = b
4 b = c
5 c = *e生成的指向图如下(其中a/b/c触发了循环坍塌):

5.6.3 波传递算法(Wave Propagation)
波传递算法的伪代码如下:
1 repeat
2 changed = false
3 collapse Strongly Connected Components
4 WAVEPROPAGATION
5 ADDNEWEDGES
6 if a new edge has been added to G then
7 changed = true
8 until changed = false
9
10
11 WAVEPROPAGATION(G, P, T)
12 while T ≠ []
13 v = hd(T)
14 Pdif = Pcur(v) – Pold(v)
15 Pold(v) = Pcur(v)
16 if Pdif ≠ {}
17 for each w such that (v, w) ∈ E do
18 Pcur(w) = Pcur(w) ∪ Pdif
19
20
21 ADDNEWEDGES(G = (E, V), C)
22 for each operation c such as l = *r ∈ C do
23 Pnew = Pcur(r) – Pcache(c)
24 Pcache(c) = Pcache(c) ∪ Pnew
25 for each v ∈ Pnew do
26 if (v, l) ∉ E then
27 E = E ∪ {(v, l)}
28 Pcur(l) = Pcur(l) ∪ Pold(v)
29 for each operation c such as *l = r do
30 Pnew = Pcur(l) – Pcache(c)
31 Pcache(c) = Pcache(c) ∪ Pnew
32 for each v ∈ Pnew do
33 if (r, v) ∉ E then
34 E = E ∪ {(r, v)}
35 Pcur(v) = Pcur(v) ∪ Pold(r)上述算法中的参数的含义如下:
- G:指向图
- P:指向集合
- T:G中所有节点的拓扑顺序
- Pcache:上一次计算出来的指向集合,初始化为{}
对下面的伪代码:
1 h = &c
2 e = &g
3 b = c
4 h = &g
5 h = a
6 c = b
7 a = &e
8 f = d
9 b = a
10 d = *h
11 *e = f
12 f = &a生成的指向图如下(其中b/c和d/f/g触发了循环坍塌):
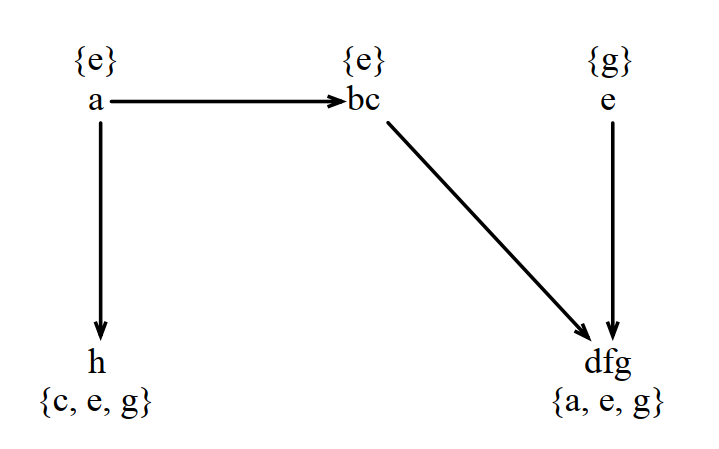
对应的堆内存拓扑图如下:
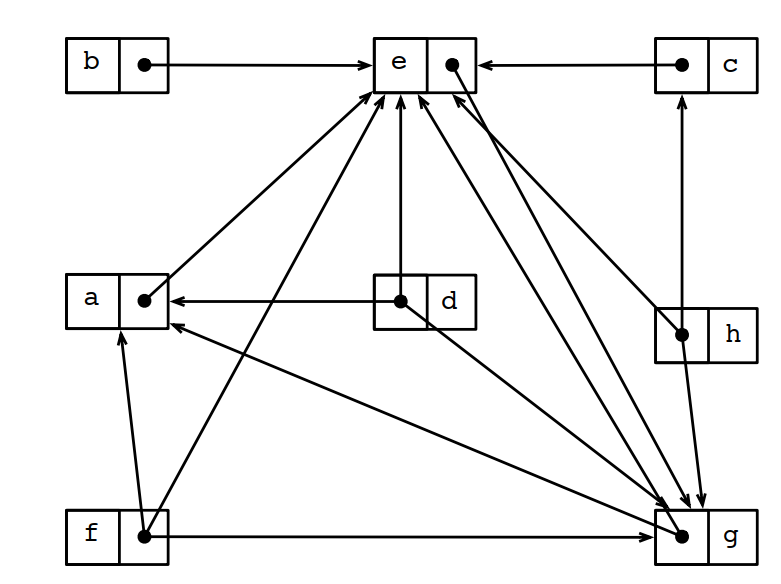
5.7 STEENSGAARD指针分析算法
如果把Anderson指针分析算法中的集合包含换成等号(将包含符号左右两侧的集合先求并集,然后赋值给原来的两个集合),就形成了Steensgaard指针分析算法,也称为基于集合并集的指针分析算法。
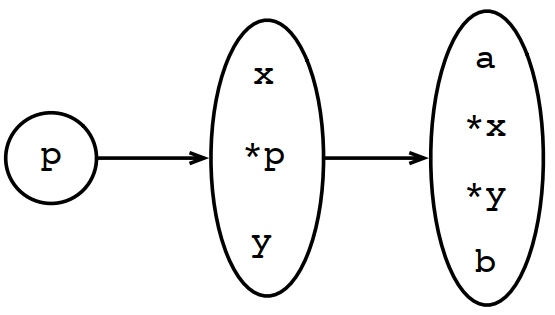
对下面的伪代码:
1 x = &a;
2 y = &b;
3 p = &x;
4 p = &y;生成的指向图如下:
5.7.1 Union-Find
基于链式并集计算的复杂度可以达到α(n),其中α是Ackermann function的简称,该算法实现也称为Union-Find。算法的具体描述参见An Improved Equivalence Algorithms (1964)。
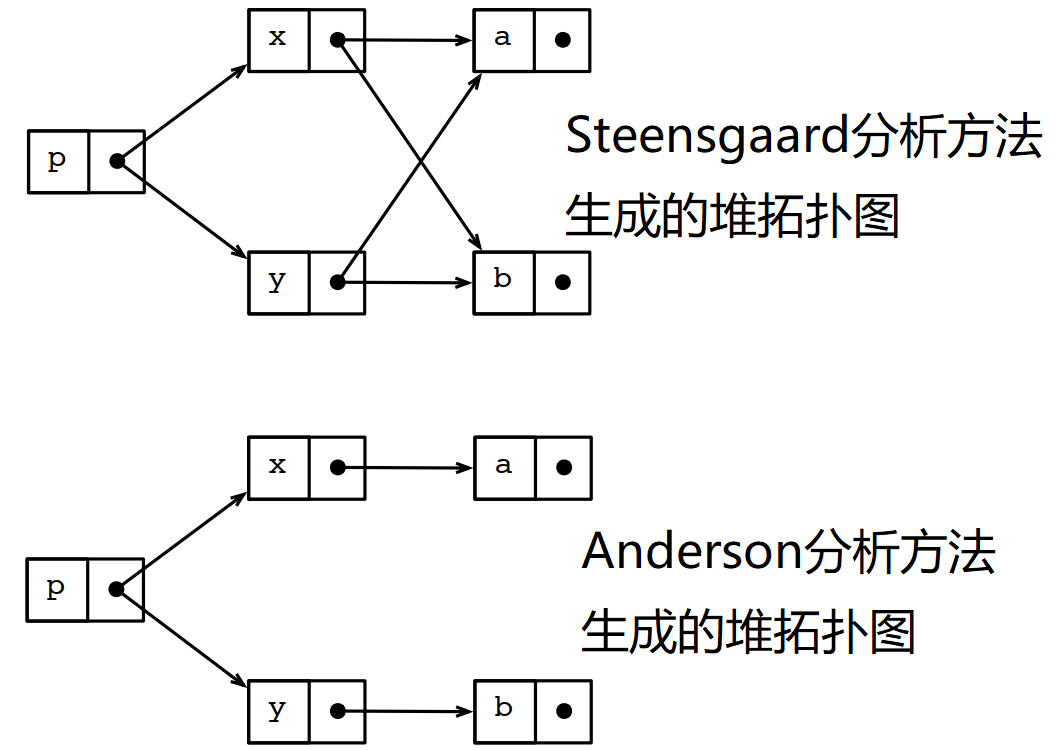
5.7.2 Steensgaard指针分析算法没有Anderson指针分析算法精准
例如上面例子生成的两个堆的拓扑图,按Steensgaard的分析结论,x可能指向b,y可能指向a。但Anderson的分析结论,x不可能指向b,y不可能指向a,显然Anderson的分析结论更接近事实。
5.8 总结
5.8.1 一种通用模式(A Common Pattern)
迄今为止,所有分析算法都遵循一种模式:迭代,直到找到一个不动点(也就是说,如果某次迭代后,所有变量都不变,后面再触发迭代,也不会再改变)。
这个通用模式适用于数据流分析、控制流分析和指向分析。
5.8.2 流相关性(Flow Sensitiveness)
尽管Anderson分析算法比Steensgaard算法精确,但由于它是流无关算法,所以仍然存在一些结论是实际运行中不可能出现,或者不可能同时出现的,这就是流无关分析算法(Flow Insensitive)的局限性。
但是如果按照流相关分析算法(Flow Sensitive)进行分析,每个程序点都需要保留一份独立的分析结论,这对大规模程序的分析是非常昂贵的(常常会带来OOM:))。
5.8.3 指针分析简史
- Andersen, L. "Program Analysis and Specialization for the C Programming Language", PhD Thesis, University of Copenhagen, (1994)
- Hardekopf, B. and Lin, C. "The Ant and the Grasshopper: fast and accurate pointer analysis for millions of lines of code", PLDI, pp 290-299 (2007)
- Pereira, F. and Berlin, D. "Wave Propagation and Deep Propagation for Pointer Analysis", CGO, pp 126-135 (2009)
- Steensgaard, B., "Points-to Analysis in Almost Linear Time", POPL, pp 32-41 (1995)
转载请注明:xuhss » 程序分析与优化 – 5 指针分析