? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
论文信息
论文标题:Iterative Graph Self-Distillation论文作者:Hanlin Zhang, Shuai Lin, Weiyang Liu, Pan Zhou, Jian Tang, Xiaodan Liang, Eric P. Xing论文来源:2021, ICLR论文地址:download 论文代码:download
1 Introduction
创新点:图级对比。
2 Method
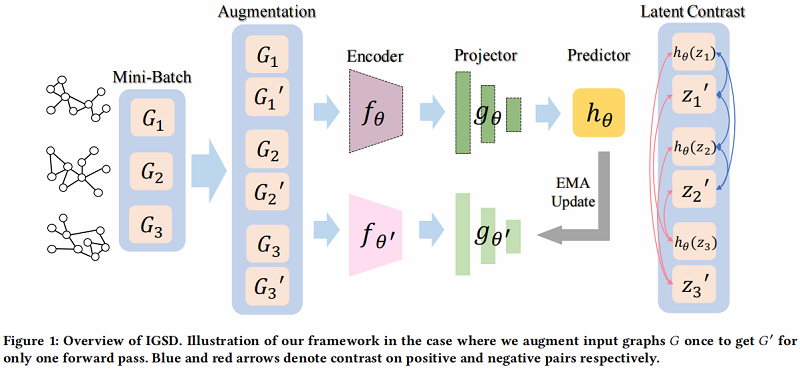
整体框架如下:
2.1 Iterative Graph Self-Distillation Framework
在 IGSD 中,引入了一个结构相似的两个网络,由 encoder fθfθf_{\theta}、projector gθgθg_{\theta} 和 predictor hθhθh_{\theta} 组成。我们将教师网络和学生网络的组成部分分别表示为 fθ′fθ′f_{\theta^{\prime}}、gθ′gθ′g_{\theta^{\prime}} 和 fθfθf_{\theta}、gθgθg_{\theta}、hθhθh_{\theta}
IGSD 过程描述如下:
-
- 首先对原始输入图 GjGjG_{j} 进行扩充,以获得增广视图 G′jGj′G_{j}^{\prime}。然后将 G′jGj′G_{j}^{\prime} 和不同的图实例 GiGiG_{i} 分别输入到两个编码器 fθfθf_{\theta}、fθ′fθ′f_{\theta^{\prime}} 中,用于提取图表示 h,h′=fθ(Gi),fθ′(G′j)h,h′=fθ(Gi),fθ′(Gj′)\boldsymbol{h}, \boldsymbol{h}^{\prime}=f_{\theta}\left(G_{i}\right), f_{\theta^{\prime}}\left(G_{j}^{\prime}\right) ;
- 其次,投影头 gθgθg_{\theta},gθ′gθ′g_{\theta^{\prime}} 通过 z=gθ(h)=W(2)σ(W(1)h)z=gθ(h)=W(2)σ(W(1)h)z=g_{\theta}(\boldsymbol{h})=W^{(2)} \sigma\left(W^{(1)} \boldsymbol{h}\right) 和 z′=gθ′(h′)=W′(2)σ(W′(1)h′)z′=gθ′(h′)=W′(2)σ(W′(1)h′)z^{\prime}=g_{\theta^{\prime}}\left(\boldsymbol{h}^{\prime}\right)=W^{\prime(2)} \sigma\left(W^{\prime(1)} \boldsymbol{h}^{\prime}\right) 转换图表示 h,h′h,h′\boldsymbol{h}, \boldsymbol{h}^{\prime} 到投影 zzz,z′z′z^{\prime},其中 σσ\sigma 表示ReLU非线性;
- 最后,为防止崩溃为一个平凡的解,在学生网络中使用预测头来获得投影 zzz 的预测 hθ(z)=W(2)hσ(W(1)hz)hθ(z)=Wh(2)σ(Wh(1)z)h_{\theta}(z)=W_{h}^{(2)} \sigma\left(W_{h}^{(1)} z\right) ;
通过对称传递两个图实列 GiGiG_{i} 和 GjGjG_{j},可以得到总体一致性损失:
Lcon (Gi,Gj)=∥∥hθ(zi)−z′j∥∥22+∥∥hθ(z′i)−zj∥∥22(2)Lcon (Gi,Gj)=‖hθ(zi)−zj′‖22+‖hθ(zi′)−zj‖22(2)\mathcal{L}^{\text {con }}\left(G_{i}, G_{j}\right)=\left|h_{\theta}\left(z_{i}\right)-z_{j}^{\prime}\right|_{2}^{2}+\left|h_{\theta}\left(z_{i}^{\prime}\right)-z_{j}\right|_{2}^{2}\quad\quad\quad(2)
在一致性损失的情况下,teacher network 提供了一个回归目标来训练 student network,在通过梯度下降更新 student network 的权值后,将其参数 θ′θ′\theta^{\prime} 更新为学生参数 θθ\theta 的指数移动平均值(EMA):
θ′t←τθ′t−1+(1−τ)θt(3)θt′←τθt−1′+(1−τ)θt(3)\theta_{t}^{\prime} \leftarrow \tau \theta_{t-1}^{\prime}+(1-\tau) \theta_{t}\quad\quad\quad(3)
2.2 Self-supervised Learning with IGSD
给定一组无标记图 G={Gi}Ni=1G={Gi}i=1N\mathcal{G}=\left{G_{i}\right}_{i=1}^{N},我们的目标是学习每个图 Gi∈GGi∈GG_{i} \in \mathcal{G} 的低维表示,有利于下游任务,如图分类。
在 IGSD 中,为了对比锚定 GiGiG_{i} 与其他图实例GjGjG_{j}(即负样本),使用以下自监督的 InfoNCE 目标:
Lself-sup =−EGi∼G[logexp(−Lconi,i)exp(−Lconi,i)+∑N−1j=1Ii≠j⋅exp(−Lconi,j)]Lself-sup =−EGi∼G[logexp(−Li,icon)exp(−Li,icon)+∑j=1N−1Ii≠j⋅exp(−Li,jcon)]{\large \mathcal{L}^{\text {self-sup }}=-\mathbb{E}_{G_{i} \sim \mathcal{G}}\left[\log \frac{\exp \left(-\mathcal{L}_{i, i}^{\mathrm{con}}\right)}{\exp \left(-\mathcal{L}_{i, i}^{\mathrm{con}}\right)+\sum_{j=1}^{N-1} \mathbb{I}_{i \neq j} \cdot \exp \left(-\mathcal{L}_{i, j}^{\mathrm{con}}\right)}\right]}
其中,Lcon i,j=Lcon (Gi,Gj)Li,jcon =Lcon (Gi,Gj)\mathcal{L}_{i, j}^{\text {con }}=\mathcal{L}^{\text {con }}\left(G_{i}, G_{j}\right) 。
我们通过用混合函数 Mixλ(a,b)=λ⋅a+(1−λ)⋅bMixλ(a,b)=λ⋅a+(1−λ)⋅b\operatorname{Mix}_{\lambda}(a, b)=\lambda \cdot a+(1-\lambda) \cdot b:融合潜在表示 h=fθ(G)h=fθ(G)\boldsymbol{h}=f_{\theta}(G) 和 h′=fθ′(G)h′=fθ′(G)\boldsymbol{h}^{\prime}=f_{\theta^{\prime}}(G),得到图表示 h~h~\tilde{\boldsymbol{h}} :
h~=Mixλ(h,h′)h~=Mixλ(h,h′)\tilde{\boldsymbol{h}}=\operatorname{Mix}_{\lambda}\left(\boldsymbol{h}, \boldsymbol{h}^{\prime}\right)
2.3 Semi-supervised Learning with IGSD
考虑一个整个数据集 G=GL∪GUG=GL∪GU\mathcal{G}=\mathcal{G}_{L} \cup \mathcal{G}_{U} 由标记数据 GL={(Gi,yi)}li=1GL={(Gi,yi)}i=1l\mathcal{G}_{L}= \left{\left(G_{i}, y_{i}\right)\right}_{i=1}^{l} 和未标记数据 GU={Gi}l+ui=l+1GU={Gi}i=l+1l+uG_{U}=\left{G_{i}\right}_{i=l+1}^{l+u} (通常 u≫lu≫lu \gg l ),我们的目标是学习一个模型,可以对不可见图的图标签进行预测。生成 KKK 个增强视图,我们得到了 G′L={(G′k,y′k)}Klk=1GL′={(Gk′,yk′)}k=1Kl \mathcal{G}_{L}^{\prime}= \left{\left(G_{k}^{\prime}, y_{k}^{\prime}\right)\right}_{k=1}^{K l} 和 G′U={G′k}K(l+u)k=l+1GU′={Gk′}k=l+1K(l+u)\mathcal{G}_{U}^{\prime}=\left{G_{k}^{\prime}\right}_{k=l+1}^{K(l+u)} 作为我们的训练数据。
为了弥合自监督的预训练和下游任务之间的差距,我们将我们的模型扩展到半监督设置。在这种情况下,可以直接插入自监督损失作为表示学习的正则化器。然而,局限于标准监督学习的实例性监督可能会导致有偏的负抽样问题。为解决这一问题,我们可以使用少量的标记数据来进一步推广相似性损失,以处理属于同一类的任意数量的正样本:
Lsupcon =∑i=1Kl1KNy′i∑j=1KlIi≠j⋅Iy′i=y′j⋅Lcon (Gi,Gj)(5)Lsupcon =∑i=1Kl1KNyi′∑j=1KlIi≠j⋅Iyi′=yj′⋅Lcon (Gi,Gj)(5)\mathcal{L}^{\text {supcon }}=\sum\limits_{i=1}^{K l} \frac{1}{K N_{y_{i}^{\prime}}} \sum\limits_{j=1}^{K l} \mathbb{I}_{i \neq j} \cdot \mathbb{I}_{y_{i}^{\prime}=y_{j}^{\prime}} \cdot \mathcal{L}^{\text {con }}\left(G_{i}, G_{j}\right)\quad\quad\quad(5)
其中,Ny′iNyi′N_{y_{i}^{\prime}} 表示训练集中与锚点 iii 具有相同标签 y′iyi′y_{i}^{\prime} 的样本总数。由于IGSD的图级对比性质,我们能够缓解带有监督对比损失的有偏负抽样问题,这是至关重要的,但在大多数 context-instance 对比学习模型中无法实现,因为子图通常很难给其分配标签。此外,有了这种损失,我们就能够使用自我训练来有效地调整我们的模型,其中伪标签被迭代地分配给未标记的数据。
对于交叉熵或均方误差 L(GL,θ)L(GL,θ)\mathcal{L}\left(\mathcal{G}_{L}, \theta\right) ,总体目标可以总结为:
Lsemi =L(GL,θ)+wLself-sup (GL∪GU,θ)+w′Lsupcon (GL,θ)(6)Lsemi =L(GL,θ)+wLself-sup (GL∪GU,θ)+w′Lsupcon (GL,θ)(6)\mathcal{L}^{\text {semi }}=\mathcal{L}\left(G_{L}, \theta\right)+w \mathcal{L}^{\text {self-sup }}\left(\mathcal{G}_{L} \cup \mathcal{G}_{U}, \theta\right)+w^{\prime} \mathcal{L}^{\text {supcon }}\left(\mathcal{G}_{L}, \theta\right)\quad\quad\quad(6)
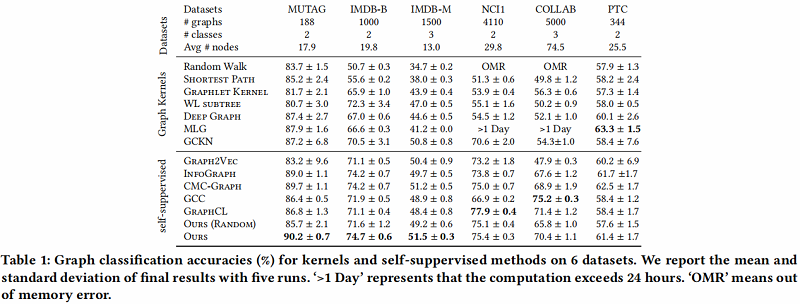
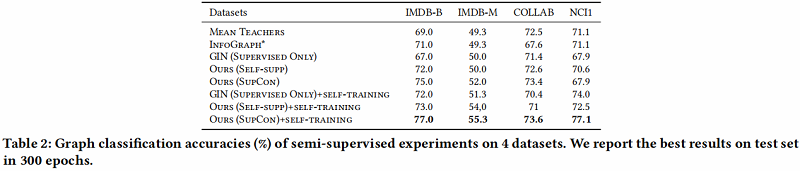
3 Experiments
节点分类
3 Conclusions
在本文中,我们提出了一种新的基于自蒸馏的图级表示学习框架IGSD。我们的框架通过对图实例的增强视图的实例识别,迭代地执行师生精馏。在自监督和半监督设置下的实验结果表明,IGSD不仅能够学习与最先进的模型竞争的表达性图表示,而且对不同的编码器和增强策略的选择也有效。在未来,我们计划将我们的框架应用到其他的图形学习任务中,并研究视图生成器的设计,以自动生成有效的视图。
-
- 1 Introduction
- 2 Method
- 2.1 Iterative Graph Self-Distillation Framework
- 2.2 Self-supervised Learning with IGSD
- 2.3 Semi-supervised Learning with IGSD
- 3 Experiments
- 3 Conclusions
__EOF__
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3RAG7O1P-1651121218730)(https://blog.csdn.net/BlairGrowing)]Blair - 本文链接: https://blog.csdn.net/BlairGrowing/p/16200705.html