? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
论文信息
论文标题:Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning论文作者:Ming Jin, Yizhen Zheng, Yuan-Fang Li, Chen Gong, Chuan Zhou, Shirui Pan论文来源:2021, IJCAI论文地址:download 论文代码:download
1 Introduction
创新:融合交叉视图对比和交叉网络对比。
2 Method
算法图示如下:
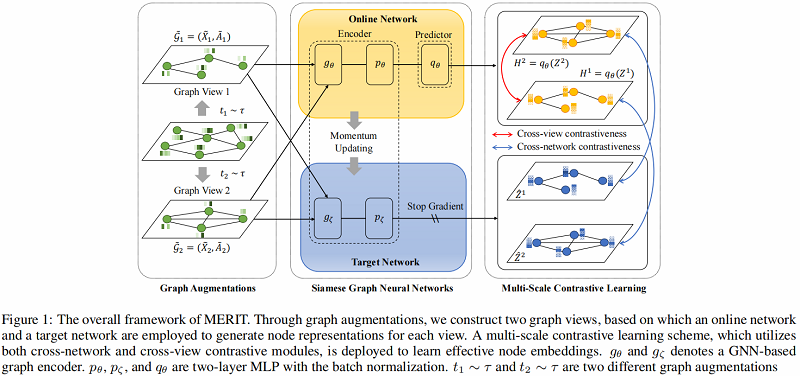
模型组成部分:
-
- Graph augmentations
- Cross-network contrastive learning
- Cross-view contrastive learning
2.1 Graph Augmentations
- Graph Diffusion (GD)
S=∞∑k=0θkTk∈RN×N(1)S=∑k=0∞θkTk∈RN×N(1)S=\sum\limits _{k=0}^{\infty} \theta_{k} T^{k} \in \mathbb{R}^{N \times N}\quad\quad\quad(1)
这里采用 PPR kernel:
S=α(I−(1−α)D−1/2AD−1/2)−1(2)S=α(I−(1−α)D−1/2AD−1/2)−1(2)S=\alpha\left(I-(1-\alpha) D^{-1 / 2} A D^{-1 / 2}\right)^{-1}\quad\quad\quad(2)
- Edge Modification (EM)
给定修改比例 PP ,先随机删除 P/2P/2 的边,再随机添加P/2P/2 的边。(添加和删除服从均匀分布)
- Subsampling (SS)
在邻接矩阵中随机选择一个节点索引作为分割点,然后使用它对原始图进行裁剪,创建一个固定大小的子图作为增广图视图。
- Node Feature Masking (NFM)
给定特征矩阵 XX 和增强比 PP,我们在 XX 中随机选择节点特征维数的 PP 部分,然后用 00 掩码它们。
在本文中,将 SS、EM 和 NFM 应用于第一个视图,并将 SS+GD+NFM 应用于第二个视图。
2.2 Cross-Network Contrastive Learning
MERIT 引入了一个孪生网络架构,它由两个相同的编码器(即 gθg_{\theta}, pθp_{\theta}, gζg_{\zeta} 和 pζp_{\zeta})组成,在 online encoder 上有一个额外的预测器qθq_{\theta},如 Figure 1 所示。
这种对比性的学习过程如 Figure 2(a) 所示:
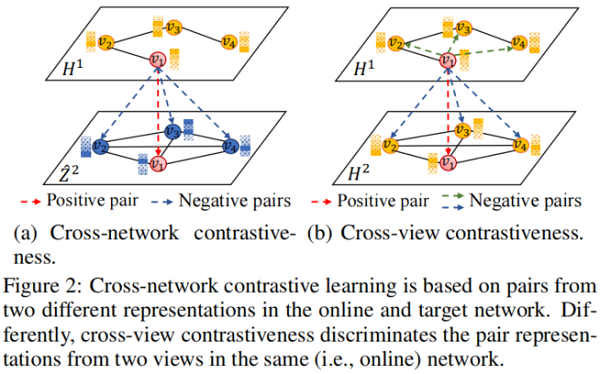
其中:
-
- H1=qθ(Z1)H^{1}=q_{\theta}\left(Z^{1}\right)
- Z1=pθ(gθ(˜X1,˜A1))Z^{1}=p_{\theta}\left(g_{\theta}\left(\tilde{X}_{1}, \tilde{A}_{1}\right)\right)
- Z2=pθ(gθ(˜X2,˜A2))Z^{2}=p_{\theta}\left(g_{\theta}\left(\tilde{X}_{2}, \tilde{A}_{2}\right)\right)
- ˆZ1=pζ(gζ(˜X1,˜A1))\hat{Z}^{1}=p_{\zeta}\left(g_{\zeta}\left(\tilde{X}_{1}, \tilde{A}_{1}\right)\right)
- ˆZ2=pζ(gζ(˜X2,˜A2))\hat{Z}^{2}=p_{\zeta}\left(g_{\zeta}\left(\tilde{X}_{2}, \tilde{A}_{2}\right)\right)
参数更新策略(动量更新机制):
ζt=m⋅ζt−1+(1−m)⋅θt(3)\zeta^{t}=m \cdot \zeta^{t-1}+(1-m) \cdot \theta^{t}\quad\quad\quad(3)
其中,mm、ζ\zeta、θ\theta 分别为动量参数、target network 参数和 online network 参数。
损失函数如下:
Lcn=12NN∑i=1(L1cn(vi)+L2cn(vi))(6)\mathcal{L}_{c n}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left(\mathcal{L}_{c n}^{1}\left(v_{i}\right)+\mathcal{L}_{c n}^{2}\left(v_{i}\right)\right)\quad\quad\quad(6)
其中:
L1cn(vi)=−logexp(sim(h1vi,ˆz2vi))∑Nj=1exp(sim(h1vi,ˆz2vj))(4)\mathcal{L}_{c n}^{1}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, \hat{z}_{v_{i}}^{2}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, \hat{z}_{v_{j}}^{2}\right)\right)}}\quad\quad\quad(4)
L2cn(vi)=−logexp(sim(h2vi,ˆz1vi))∑Nj=1exp(sim(h2vi,ˆz1vj))(5)\mathcal{L}_{c n}^{2}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{2}, \hat{z}_{v_{i}}^{1}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{2}, \hat{z}_{v_{j}}^{1}\right)\right)}}\quad\quad\quad(5)
2.3 Cross-View Contrastive Learning
损失函数:
Lkcv(vi)=Lkintra (vi)+Lkinter (vi),k∈{1,2}(10)\mathcal{L}_{c v}^{k}\left(v_{i}\right)=\mathcal{L}_{\text {intra }}^{k}\left(v_{i}\right)+\mathcal{L}_{\text {inter }}^{k}\left(v_{i}\right), \quad k \in{1,2}\quad\quad\quad(10)
其中:
Lcv=12NN∑i=1(L1cv(vi)+L2cv(vi))(9)\mathcal{L}_{c v}=\frac{1}{2 N} \sum\limits _{i=1}^{N}\left(\mathcal{L}_{c v}^{1}\left(v_{i}\right)+\mathcal{L}_{c v}^{2}\left(v_{i}\right)\right)\quad\quad\quad(9)
L1inter (vi)=−logexp(sim(h1vi,h2vi))∑Nj=1exp(sim(h1vi,h2vj))(7)\mathcal{L}_{\text {inter }}^{1}\left(v_{i}\right)=-\log {\large \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)}{\sum_{j=1}^{N} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{j}}^{2}\right)\right)}}\quad\quad\quad(7)
L1intra(vi)=−logexp(sim(h1vi,h2vi))exp(sim(h1vi,h2vi))+ΦΦ=N∑j=11i≠jexp(sim(h1vi,h1vj))(8)\begin{aligned}\mathcal{L}_{i n t r a}^{1}\left(v_{i}\right) &=-\log \frac{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)}{\exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{i}}^{2}\right)\right)+\Phi} \\Phi &=\sum\limits_{j=1}^{N} \mathbb{1}_{i \neq j} \exp \left(\operatorname{sim}\left(h_{v_{i}}^{1}, h_{v_{j}}^{1}\right)\right)\end{aligned}\quad\quad\quad(8)
2.4 Model Training
L=βLcv+(1−β)Lcn(11)\mathcal{L}=\beta \mathcal{L}_{c v}+(1-\beta) \mathcal{L}_{c n}\quad\quad\quad(11)
3 Experiment
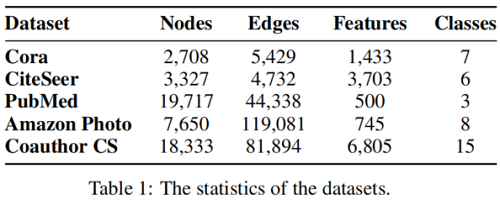
数据集
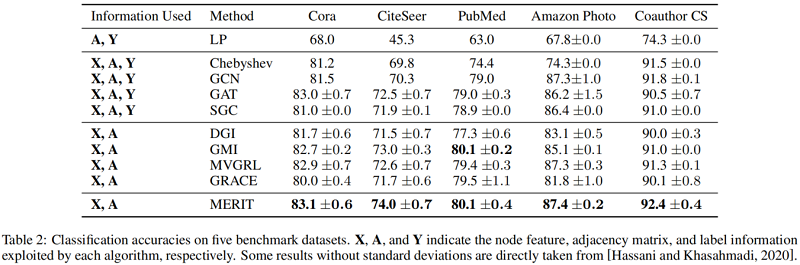
基线实验
-
- 1 Introduction
- 2 Method
- 2.1 Graph Augmentations
- 2.2 Cross-Network Contrastive Learning
- 2.3 Cross-View Contrastive Learning
- 2.4 Model Training
- 3 Experiment
__EOF__
- 本文作者: Blair
- 本文链接: https://blog.csdn.net/BlairGrowing/p/16196841.html
- 关于博主: 评论和私信会在第一时间回复。或者直接私信我。
- 版权声明: 本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
- 声援博主: 如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。
转载请注明:xuhss » 论文解读(MERIT)《Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning》