? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
14 TEMPORAL GRAPH NETWORKS FOR DEEP LEARNING ON DYNAMIC GRAPHS
Abstract
提出了时间图网络(TGNs),一个通用的,有效的框架,在动态图上的深度学习表示为时序事件序列。由于记忆模块和基于图的操作的新颖组合,TGN在计算效率更高的同时,显著优于以前的方法。
Conclusion
本文介绍了连续时间动态图学习的通用框架TGN。我们在多个任务和数据集上获得了最先进的结果,同时比以前的方法更快。
详细的消融研究表明,记忆及其相关模块对存储长期信息的重要性,以及基于图的嵌入模块对生成最新节点嵌入的重要性。
Figure and table
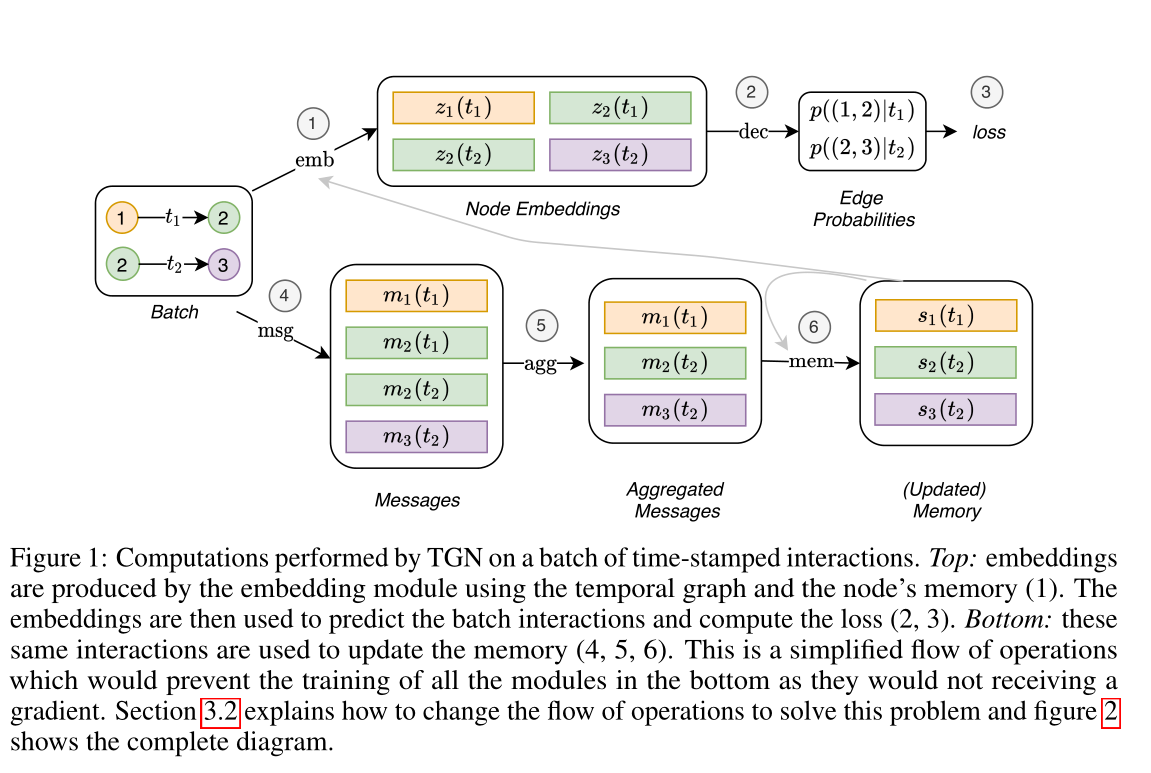
图1 由TGN对一批带时间戳的交互进行的计算。上方:嵌入由嵌入模块使用时间图和节点的记忆(1)产生。然后,嵌入用于预测批量交互和计算损失(2,3)。下方:这些相同的交互用于更新内存(4,5,6)。这是一个简化的操作流程,将防止下方所有模块的训练,因为它们不会接收到梯度。第3.2节解释了如何更改操作流程以解决此问题,图2显示了完整的关系图。
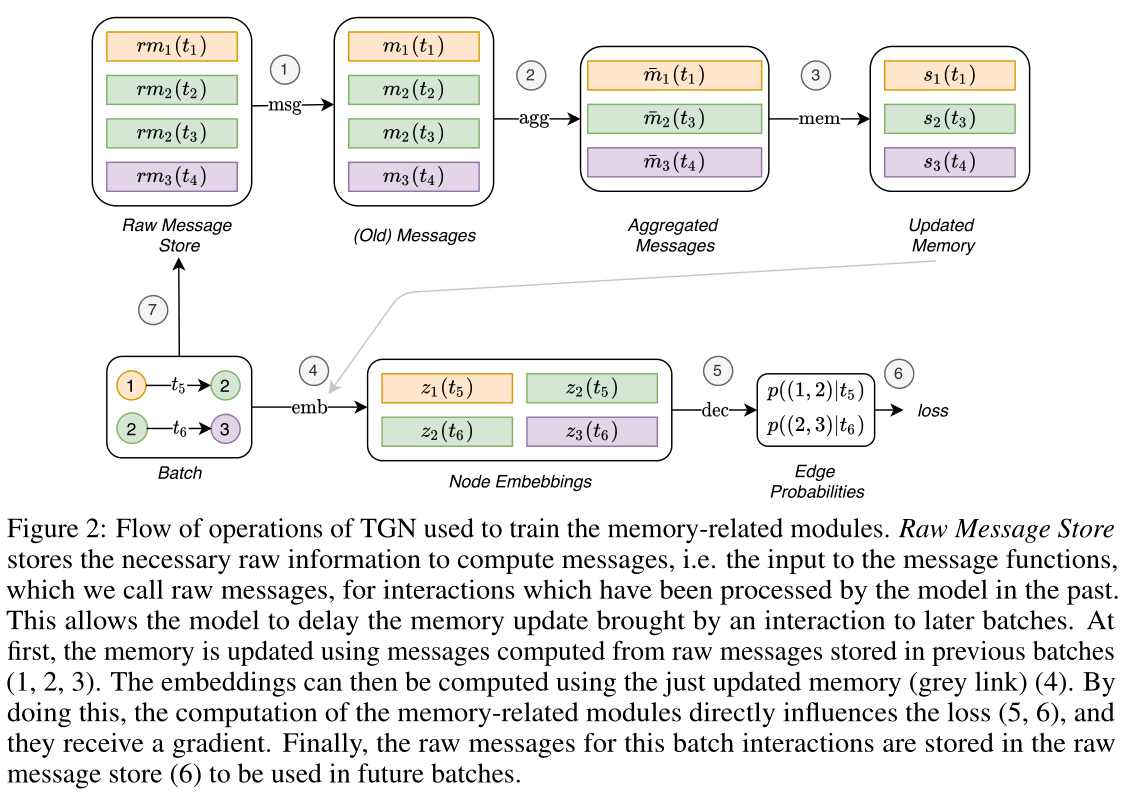
图2:TGN用于训练记忆相关模块的操作流程。原始消息存储(Raw Message Store)存储计算消息所需的原始信息,即消息函数的输入,我们称之为原始消息,用于模型过去处理过的交互。
这允许模型将交互带来的记忆更新延迟到以后的批处理中。首先,使用从前几批(1,2,3)中存储的原始消息计算出来的消息更新内存。然后,可以使用刚刚更新的记忆(灰色箭头)计算嵌入(4)。通过这样做,记忆相关模块的计算直接影响损失(5,6)。最后,用于此批处理交互的原始消息存储在原始消息存储(7)中,以便在未来的批处理中使用。
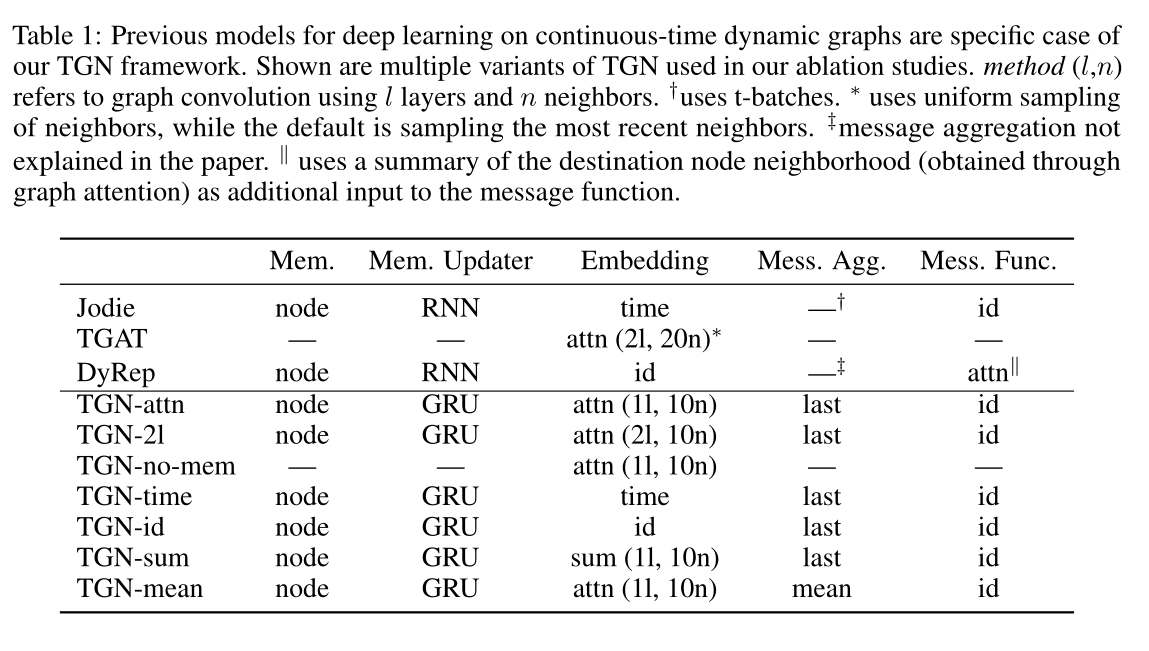
表1 以往的连续时间动态图深度学习模型都是TGN框架的具体案例。图中显示的是消融研究中使用的多种TGN变体。method(l,n)是指使用l层和n个邻居的图卷积。††使用t-batch。∗∗使用邻居的均匀抽样,而默认是抽样最近的邻居。‡‡表示本文中没有解释消息聚合。||||表示使用目标节点邻域的求和(通过图注意力获得)作为消息函数的附加输入。
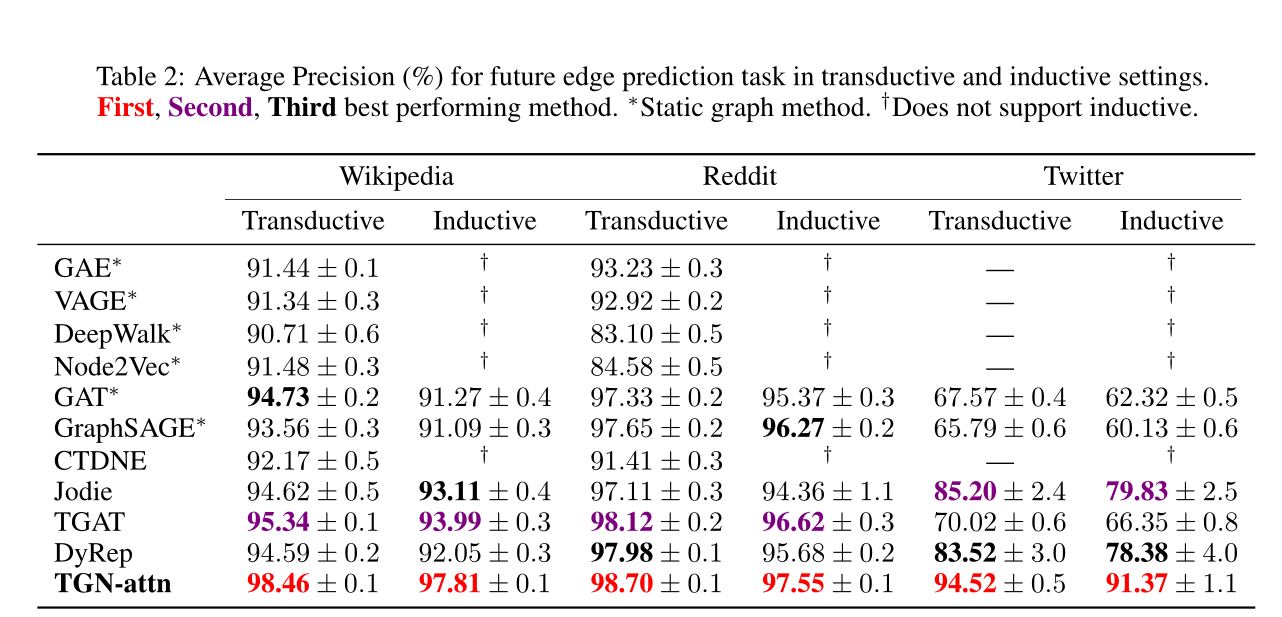
表2:在transductive和inductive设置下,未来边缘预测任务的平均精度(%)。∗表示静态图的方法。†表示不支持归纳。
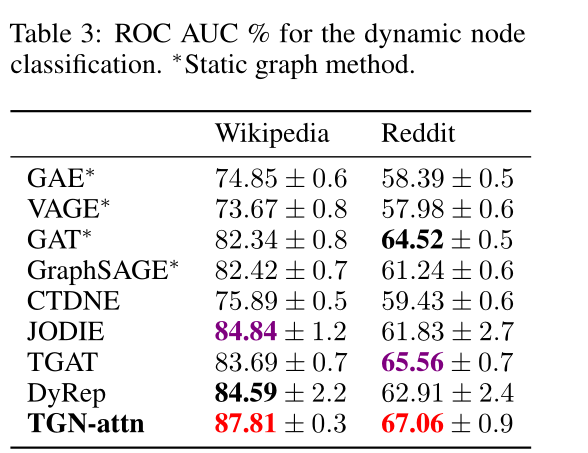
表3 动态节点分类的ROC AUC %。∗表示静态图的方法。
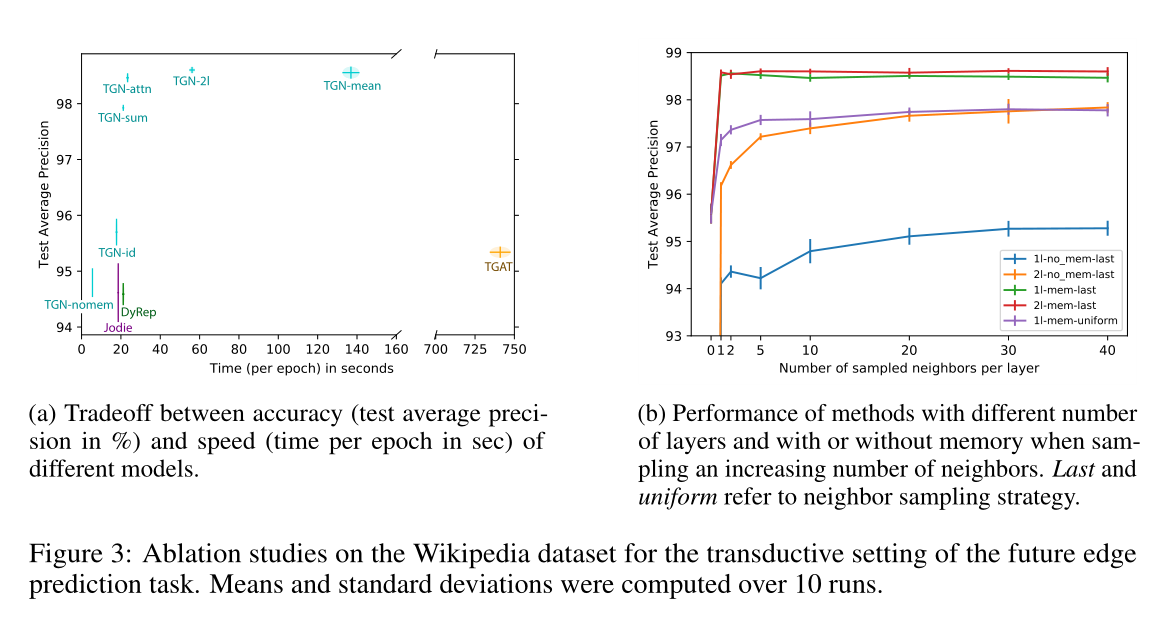
图3 以transductive方式在维基百科数据集上的消融实验,用于未来边缘预测任务。计算平均值和标准差超过10次。
(a)不同模型的精度(以%为单位的测试平均精度)和速度(以秒为单位的epoch时间)之间的权衡。
(b)随着邻居数量的增加,不同层数、有无记忆的方法的性能。最后统一采用邻居抽样策略。
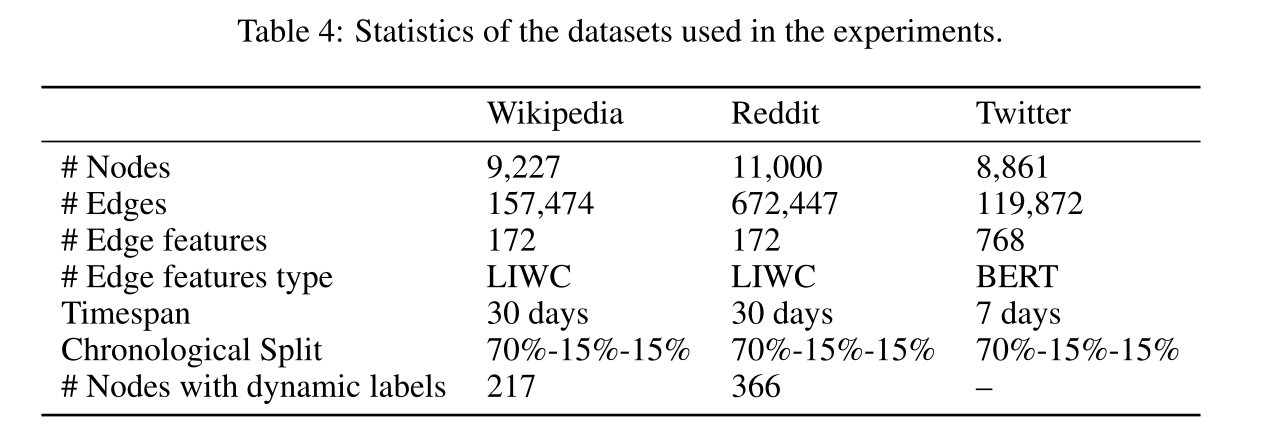
表4 实验数据集的参数。
Introduction
在图上进行深度学习的大多数方法都假设底层图是静态的。然而,现实生活中的大多数互动系统,如社会网络或生物互动体,都是动态的。
贡献:在本文中提出了时间图网络(tgn)的通用归纳框架,该框架作用于以事件序列表示的连续时间动态图,并表明以前的许多方法都是tgn的具体实例。其次,提出了一种新的训练策略,允许模型从数据的顺序中学习,同时保持高效的并行处理。第三,我们对我们的框架的不同组成部分进行了详细的消融实验,并分析了速度和精度之间的权衡。
Method
2 BACKGROUND
静态图的深度学习:一个静态图G=(V,E)\mathcal{G = (V, E)}由节点V={1,…,n}\mathcal{V} ={ 1,…, n }和边E⊆V×V\mathcal{E⊆V × V}构成,它们被赋予特征,分别用Vi\mathbf{V}_i和eij\mathbf{e}_{ij}表示,其中i,j=1,...,ni,j=1,...,n。典型的图神经网络(GNN)通过学习一种形式的局部聚合规则来创建节点的嵌入zi\mathbf{z}_{i}
zi=∑j∈nih(mij,vi)mij=msg(vi,vj,eij)\mathbf{z}_{i}=\sum_{j \in n_{i}} h\left(\mathbf{m}_{i j}, \mathbf{v}_{i}\right) \quad \mathbf{m}_{i j}=\operatorname{msg}\left(\mathbf{v}_{i}, \mathbf{v}_{j}, \mathbf{e}_{i j}\right)
它被解释为从邻居jj传递到节点ii的消息,此处ni={j:(i,j)∈E}n_i={ j:(i,j) \in \mathcal{E} }表示节点ii和MSG(消息)的邻居,hh为可学习函数。
动态图:动态图主要有两种模型。离散时间动态图(DTDG)是在一定时间间隔内拍摄的静态图快照序列。连续时间动态图(CTDG)更为通用,可以表示为事件的时间列表,包括边的添加或删除、节点的添加或删除以及节点或边缘特征转换。
本文的时间图被建模为时间戳事件序列G={x(t1),x(t2),…}\mathcal{G} = { x(t_1), x(t_2),…},表示一个节点的添加或更改,或一对节点在时间0≤t1≤t2≤...0≤t1≤t2≤...时的交互。事件x(t)x(t)可以有两种类型:
1)节点事件由vi(t)\mathbf{v}_i(t)表示,其中ii表示节点的索引,v\mathbf{v}是与事件相关的向量属性。如果索引ii以前没有出现过,事件创建节点ii(带有给定的特征),否则它更新特征。
2)节点ii和jj之间的交互事件用一个(有向的)时间边eij(t)\mathbf{e}_{ij}(t)表示(在一对节点之间可能有不止一条边,所以技术上这是一个多重图)。
分别通过V(T)={i:∃vi(t)∈G,t∈T}\mathcal{V}(T)=\left{i: \exists \mathbf{v}_{i}(t) \in \mathcal{G}, t \in T\right}和E(T)={(i,j):∃eij(t)∈G,t∈T}\mathcal{E}(T)=\left{(i, j): \exists \mathbf{e}_{i j}(t) \in \mathscr{\mathcal { G }}, t \in T\right}来表示顶点和边的时间集合,通过ni(T)={j:(i,j)∈E(T)}n_{i}(T)={j:(i, j) \in \mathcal{E}(T)}表示节点ii在时间间隔TT中的邻居。nki(T)n^k_i(T)表示k跳邻居。时间图G\mathcal{G}在tt时刻的快照是具有n(t)n(t)个节点的多重图G(t)=(V[0,t],E[0,t])\mathcal{G}(t) = (\mathcal{V}[0, t], \mathcal{E}[0, t])。删除事件在附录A.1中进行了讨论。
3 TEMPORAL GRAPH NETWORKS
根据(Representation learning for dynamic graphs: A survey)中的观点,动态图的神经模型可以被视为编码器-解码器对,其中编码器是一个函数,从动态图映射到节点嵌入,解码器将一个或多个节点嵌入作为输入,并进行特定于任务的预测,如节点分类或链接预测。本文的主要贡献是一种新颖的时间图网络(TGN)编码器,它应用于一个连续时间动态图,表示为一个时间戳事件序列,并在每个时间t时,得到图节点嵌入Z(t)=(z1(t),...,zn(t)(t))\mathbf{Z}(t)=(\mathbf{z}_1(t),...,\mathbf{z}_{n(t)}(t))。
3.1 CORE MODULES
记忆模块:时间tt时模型的记忆(状态)由向量si(t)\mathbf{s}_i(t)组成,用于模型到目前为止观察到的每个节点ii。一个节点的记忆在事件发生后更新(例如与另一个节点交互或节点发生变化),它的目的是用压缩格式表示该节点的历史。由于这个特定的模块,tgn能够记住图中每个节点的长期依赖关系。当遇到一个新节点时,它的内存将被初始化为零向量,然后为涉及该节点的每个事件更新它,即使在模型完成训练之后,记忆模块依旧保持更新。
还可以在模型中添加全局(图级别)记忆,以跟踪整个网络的演化,本文将此作为未来的工作。
消息函数:对于涉及节点ii的每个事件,都会计算一条消息来更新ii的记忆。当源节点ii和目标节点jj在时间tt发生交互事件eij(t)\mathbf{e}_{ij}(t)时,可以计算两条消息:
mi(t)=msgs(si(t−),sj(t−),Δt,eij(t)),mj(t)=msgd(sj(t−),si(t−),Δt,eij(t))\mathbf{m}_{i}(t)=\operatorname{msg}_{\mathrm{s}}\left(\mathbf{s}_{i}\left(t^{-}\right), \mathbf{s}_{j}\left(t^{-}\right), \Delta t, \mathbf{e}_{i j}(t)\right), \quad \mathbf{m}_{j}(t)=\operatorname{msg}_{\mathrm{d}}\left(\mathbf{s}_{j}\left(t^{-}\right), \mathbf{s}_{i}\left(t^{-}\right), \Delta t, \mathbf{e}_{i j}(t)\right)
类似地,对于节点级事件vi(t)\mathbf{v}_i(t),可以为涉及事件的节点计算单个消息:
mi(t)=msgn(si(t−),t,vi(t))\mathbf{m}_{i}(t)=\operatorname{msg}_{\mathrm{n}}\left(\mathbf{s}_{i}\left(t^{-}\right), t, \mathbf{v}_{i}(t)\right)
其中si(t−)\mathbf{s}_{i}(t^{-})是节点ii在时间tt之前的记忆(即从之前涉及ii的交互开始的时间)
msgs,msgd,msgn\operatorname{msg}_{\mathrm{s}},\operatorname{msg}_{\mathrm{d}},\operatorname{msg}_{\mathrm{n}}是可学的消息函数,例如MLP。在所有的实验中,为了简单起见,我们选择消息函数作为标识(id),它只是输入的连接。该框架还支持删除事件,在附录A.1中有介绍。
消息聚合器:由于效率原因而采用批处理可能会导致在同一批处理中涉及同一节点ii的多个事件。在本文的公式中,每个事件都会生成一条消息,我们使用一种机制来聚合消息:mi(t1),...,mi(tb)\mathbf{m}_{i}(t_1),...,\mathbf{m}_{i}(t_b),其中t1,...,tB≤t t_1,...,t_B≤t
ˉmi(t)=agg(mi(t1),...,mi(tb))\bar{\mathbf{m}}_i(t)=\operatorname{agg}(\mathbf{m}_{i}(t_1),...,\mathbf{m}_{i}(t_b))
这里,agg是一个聚合函数。虽然实现此模块可以考虑多种选择(例如rnn或attention),但为了简单起见,我们在实验中考虑了两种有效的不可学习(即无法BP)解决方案:最新消息(只保留给定节点的最新消息)和平均消息(对给定节点的所有消息进行平均)。我们将可学习聚合作为未来的研究方向。
记忆更新:如前所述,每个涉及节点自身的事件都会更新节点的记忆:
si(t)=mem(ˉmi(t),si(t−))\mathbf{s}_{i}(t)=\operatorname{mem}(\bar{\mathbf{m}}_i(t),\mathbf{s}_{i}(t^{-}))
对于涉及两个节点ii和jj的交互事件,在事件发生后更新两个节点的记忆。对于节点级事件,只更新相关节点的记忆(不对邻居做更新操作)。在这里,mem是一个可学习的记忆更新函数,例如一个RNN,如LSTM 或GRU 。
嵌入:嵌入模块用于生成节点ii在任意时刻tt的时间嵌入zi\mathbf{z}_{i}。嵌入模块的主要目标是避免所谓的记忆陈旧问题(Kazemi et al., 2020)。由于节点ii的内存只在该节点参与某个事件时才会更新,因此,在长时间没有事件发生的情况下(例如,社交网络用户在再次活跃之前停止使用该平台一段时间),ii的内存就会变得陈旧。虽然嵌入模块可以有多种实现,但本文使用的形式是:
zi(t)=emb(i,t)=∑j∈nki([0,t])h(si(t),sj(t),eij,vi(t),vj(t))\mathbf{z}_{i}(t)=\operatorname{emb}(i, t)=\sum_{j \in n_{i}^{k}([0, t])} h\left(\mathbf{s}_{i}(t), \mathbf{s}_{j}(t), \mathbf{e}_{i j}, \mathbf{v}_{i}(t), \mathbf{v}_{j}(t)\right)
其中hh为可学习函数。嵌入函数包括许多不同的公式作为特殊情况,如下:
标志Identity (id):emb(i,t)=si(t)emb(i, t) = \mathbf{s}_{i}(t),它直接使用记忆作为节点嵌入。
事件Time projection (time):emb(i,t)=(1+Δtw)∘si(t)\operatorname{emb}(i, t)=(1+\Delta t \mathbf{w}) \circ \mathbf{s}_{i}(t),其中w\mathbf{w}是可学习的参数,∆t∆t是自上次交互以来的时间,◦◦表示元素矢量乘积。Jodie采用了这种嵌入方法。投影
时间图注意Temporal Graph Attention (attn):一系列的LL层图注意层通过聚合LL跳时间邻居的信息来计算ii的嵌入。
在第L层,该方法的输入为节点ii的表示h(l−1)i(t)\mathbf{h}_i^{(l-1)}(t),当前事件戳tt,带时间戳t1,...,tNt_1,...,t_N的节点ii邻居表示{h(l−1)1(t),...,h(l−1)N(t)}{ \mathbf{h}_1^{(l-1)}(t),...,\mathbf{h}_N^{(l-1)}(t) }和特征ei1(t1),...,eiN(tN)\mathbf{e}_{i1}(t_1),...,\mathbf{e}_{iN}(t_N),对于在ii的时间邻居中形成边的每一个考虑的相互作用
h(l)i(t)=MLP(l)(h(l−1)i(t)‖˜h(l)i(t))˜h(l)i(t)=MultiHeadAttention (l)(q(l)(t),K(l)(t),V(l)(t))q(l)(t)=h(l−1)i(t)‖ϕ(0)K(l)(t)=V(l)(t)=C(l)(t)C(l)(t)=[h(l−1)1(t)‖ei1(t1)‖ϕ(t−t1),…,h(l−1)N(t)‖eiN(tN)‖ϕ(t−tN)]\begin{aligned}
\mathbf{h}_{i}^{(l)}(t) &=\operatorname{MLP}^{(l)}\left(\mathbf{h}_{i}^{(l-1)}(t) | \tilde{\mathbf{h}}_{i}^{(l)}(t)\right) \
\tilde{\mathbf{h}}_{i}^{(l)}(t) &=\operatorname{MultiHeadAttention~}^{(l)}\left(\mathbf{q}^{(l)}(t), \mathbf{K}^{(l)}(t), \mathbf{V}^{(l)}(t)\right) \
\mathbf{q}^{(l)}(t) &=\mathbf{h}_{i}^{(l-1)}(t) | \phi(0) \
\mathbf{K}^{(l)}(t) &=\mathbf{V}^{(l)}(t)=\mathbf{C}^{(l)}(t) \
\mathbf{C}^{(l)}(t) &=\left[\mathbf{h}_{1}^{(l-1)}(t)\left|\mathbf{e}_{i 1}\left(t_{1}\right)\right| \phi\left(t-t_{1}\right), \ldots, \mathbf{h}_{N}^{(l-1)}(t)\left|\mathbf{e}_{i N}\left(t_{N}\right)\right| \phi\left(t-t_{N}\right)\right]
\end{aligned}
其中
ϕ(·)\phi(·)表示一种通用时间编码
||||是连接操作符
zi(t)=emb(i,t)=h(L)i(t)\mathbf{z}_{i}(t)=\operatorname{emb}(i, t)=\mathbf{h}_i^{(L)}(t)
每一层相当于执行多头注意,其中query(q(l)(t))(\mathbf{q}^{(l)}(t))是一个参考节点(即目标节点或其l−1l−1跳邻居之一),key(k(l)(t))(\mathbf{k}^{(l)}(t))和value(V(l)(t))(\mathbf{V}^{(l)}(t))是它的邻居。最后,利用MLP将参考节点表示与聚合信息结合起来。与该层的原始公式不同,其中没有使用节点的时间特征,在本文的情况下,每个节点的输入表示h(0)j(t)=si(t)+vi(t)\mathbf{h}^{(0) }_j(t) = \mathbf{s}_{i}(t) +\mathbf{v}_{i}(t),因此它允许模型同时利用当前内存si(t)\mathbf{s}_{i}(t)和时间节点特征vi(t)\mathbf{v}_{i}(t)。
时间图求和Temporal Graph Sum (sum):图上更简单、更快的聚合:
h(l)i(t)=W(l)2(h(l−1)i(t)‖˜h(l)i(t))˜h(l)i(t)=ReLu(∑j∈ni([0,t])W(l)1(h(l−1)j(t)‖eij‖ϕ(t−tj)))\begin{aligned}
\mathbf{h}_{i}^{(l)}(t) &=\mathbf{W}_{2}^{(l)}\left(\mathbf{h}_{i}^{(l-1)}(t) | \tilde{\mathbf{h}}_{i}^{(l)}(t)\right) \
\tilde{\mathbf{h}}_{i}^{(l)}(t) &=\operatorname{ReLu}\left(\sum_{j \in n_{i}([0, t])} \mathbf{W}_{1}^{(l)}\left(\mathbf{h}_{j}^{(l-1)}(t)\left|\mathbf{e}_{i j}\right| \phi\left(t-t_{j}\right)\right)\right)
\end{aligned}
其中,ϕ(·)\phi(·)还是一种时间编码
zi(t)=emb(i,t)=h(L)i(t)\mathbf{z}_{i}(t)=\operatorname{emb}(i, t)=\mathbf{h}_i^{(L)}(t)
在实验中,本文对时间图注意和时间图和模块都使用了Time2Vec和TGAT中提出的时间编码。
图嵌入模块通过聚合来自节点邻居内存的信息来缓解陈旧的问题。当节点处于非活动状态一段时间时,他的邻居在最近可能是活跃的,通过聚集他们的记忆,TGN可以计算节点的最新嵌入。时间图注意力还能够根据特征和时间信息选择哪个邻居更重要。
3.2 TRAINING
TGN可以训练用于各种任务,如边缘预测(自我监督)或节点分类(半监督)。以链接预测为例:提供一个时间有序的相互作用列表,目标是根据过去观察到的相互作用预测未来的相互作用。图1显示了TGN对一批训练数据进行的计算。
训练策略的复杂性与记忆相关模块(消息函数、消息聚合器和记忆更新器)有关,因为它们不会直接影响损失,因此不会接收到梯度。为了解决这个问题,必须在预测批处理交互之前更新内存。然而,在使用模型预测相同的交互作用之前,用交互作用eij(t)\mathbf{e}_{ij}(t)更新内存会导致信息泄漏。为了避免这个问题,在处理批处理时,使用来自前一批(存储在原始消息存储中)的消息更新内存,然后预测交互。图2显示了内存相关模块的训练流程。训练过程的伪代码如下。

在图2中, 在任何时间t,原始消息存储包含(最多)一个原始消息rmirm_i,用于每个节点ii,这是从时间tt之前涉及ii的最后一次交互产生的。当模型处理涉及ii的下一个交互时,它的记忆使用rmirm_i更新(图2中的箭头1、2、3),然后更新的记忆用于计算节点的嵌入和批处理损失(箭头4、5、6)。最后,新交互的原始消息存储在原始消息存储中(箭头7)。其中,给定批处理中的所有预测都可以访问相同的记忆状态。虽然从批处理中的第一个交互的角度来看,记忆是最新的(因为它包含了图中所有之前交互的信息),但从批处理中的最后一个交互的角度来看,相同的内存是过时的,因为它缺乏关于同一批处理中以前交互的信息。这就不鼓励使用大的批处理大小(在批处理大小与数据集一样大的极端情况下,所有的预测都将使用初始的零内存)。作者发现批量大小为200可以很好地平衡速度和更新粒度。
Experiment
Datasets:Wikipedia、Reddit和Twitter数据集参数见表4
Baselines:
动态图
CTDNE ,JODIE,DyRep ,TGAT
静态图
GAE ,VGAE ,DeepWalk,Node2Vec,GAT,GraphSAGE
5.1 PERFORMANCE
sota见表2
时间效率见图3a,
5.2 CHOICE OF MODULES
本节介绍消融实验,比较了TGN框架的不同实例,重点是速度与精度的权衡,由模块及其组合的选择产生。表1包含实验的变体。
此节从四个方面去对比模型变体:记忆,嵌入模块,消息聚合器,模型层数
具体的性能和时间效率见图3
Summary
整体方法还是挺简单的,读起来没什么压力,以至于感觉读了没啥感觉,创新点像作者说的可能就是以前的许多方法都是tgn的具体实例吧。
转载请注明:xuhss » 论文阅读 TEMPORAL GRAPH NETWORKS FOR DEEP LEARNING ON DYNAMIC GRAPHS