? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
1. 简介
梯度下降法是一种函数极值的优化算法。在机器学习中,主要用于寻找最小化损失函数的的最优解。是算法更新模型参数的常用的方法之一。
2. 相关概念
1. 导数
- 定义
设一元函数f(x)f(x)f(x)在x0x0x_0的临域内有定义,若极限
f‘(x0)=limΔx→0f(x+Δx)−f(x)Δf‘(x0)=limΔx→0f(x+Δx)−f(x)Δf^{
}(x\_0)=\lim\_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta } 存在,则称f‘(x0)f‘(x0)f^{}(x_0)为f(x)f(x)f(x)在x=x0x=x0x=x_0处的导数。
- 意义
- 导数的绝对值大小代表了当前函数的在该处的变化速度
- 导数的正负代表了在一定临域内随着自变量xxx的增加,函数值是增大还是减小
2. 偏导数
- 定义
对于多元函数f(x),x∈Rpf(x),x∈Rpf(x),x \in R^p,f(x)f(x)f(x)在对xixix_i的偏导数定义为
∂f(x)∂xi=limΔx→0f(x1,x2,⋯,xi+Δx,⋯,xp)−f(x1,x2,⋯,xi,⋯,xp)Δx∂f(x)∂xi=limΔx→0f(x1,x2,⋯,xi+Δx,⋯,xp)−f(x1,x2,⋯,xi,⋯,xp)Δx\frac{\partial f(x)}{\partial x_i}=\lim_{\Delta x \to 0}\frac{f(x_1,x_2,\cdots,x_i+\Delta x,\cdots,x_p)-f(x_1,x_2,\cdots,x_i,\cdots,x_p)}{\Delta x}
- 意义
偏导数定义了多元函数在某个数轴方向上的变化情况。
3. 方向导数
- 定义
函数的偏导数定义了在各个数轴上的变化率,方向导数则为函数在任意方向上的变化率。以二元函数f(x,y)f(x,y)f(x,y)为例:
∇∂f(x)∂l|(x0,y0)=∂f(x)∂xcos(α)+∂f(x)∂ycos(β)∇∂f(x)∂l|(x0,y0)=∂f(x)∂xcos(α)+∂f(x)∂ycos(β)\nabla \frac{\partial f(x)}{\partial l}|_{(x_0,y_0)}=\frac{\partial f(x)}{\partial x}\cos(\alpha)+\frac{\partial f(x)}{\partial y}\cos(\beta)
- 意义
多元函数在某点处的方向导数有无数个,每一个方向导数的值代表了在该方向上的变化程度,我们要寻找在某点处函数变化最快的方向就可以转化成寻找在该点处方向导数的绝对值最大时对应的那个方向
4. 梯度
- 定义
梯度是一个矢量,表示函数沿着该方向的变化率最大,记为
f(x)=(∂f(x)∂x1,∂f(x)∂x2,⋯,∂f(x)∂xp)Tf(x)=(∂f(x)∂x1,∂f(x)∂x2,⋯,∂f(x)∂xp)Tf(x)=(\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x_2},\cdots,\frac{\partial f(x)}{\partial x_p})^T
- 为什么该方向为变化最快的方向
根据方向导数定义,
∂f(x)∂l|(x0,y0)=∂f(x)∂xcos(α)+∂f(x)∂ycos(β)=(∂f(x)∂x,∂f(x)∂y)(cos(α),cos(β))T=A⋅I(A=(∂f(x)∂x,∂f(x)∂y),I=(cos(α),cos(β))T)=||A||×||I||cos(θ)(θ为两个向量的夹角)∂f(x)∂l|(x0,y0)=∂f(x)∂xcos(α)+∂f(x)∂ycos(β)=(∂f(x)∂x,∂f(x)∂y)(cos(α),cos(β))T=A⋅I(A=(∂f(x)∂x,∂f(x)∂y),I=(cos(α),cos(β))T)=||A||×||I||cos(θ)(θ为两个向量的夹角)\begin{align}
\frac{\partial f(x)}{\partial l}|_{(x_0,y_0)}
&=\frac{\partial f(x)}{\partial x}\cos(\alpha)+\frac{\partial f(x)}{\partial y}\cos(\beta) \
&= (\frac{\partial f(x)}{\partial x},\frac{\partial f(x)}{\partial y})(\cos(\alpha),\cos(\beta))^T \
&= A\cdot I \quad\quad (A=(\frac{\partial f(x)}{\partial x},\frac{\partial f(x)}{\partial y}),I=(\cos(\alpha),\cos(\beta))^T ) \
&= ||A||\times||I||\cos(\theta) \qquad (\theta为两个向量的夹角)
\end{align}
当且仅当 θ=0θ=0\theta=0,即AAA和III通向时,方向导数取得最大值,因此梯度表示变化率最大的方向,此时方向导数为正。因此梯度指向函数增大的方向。
3 原理详解

假设在一个类是凹函数的山中放一个小球,让它自然的滚动到山谷(最小值点)处,那么小球滚动每个地点滚动的方向都是梯度的负方向。
现在有一个凹函数,要找到它的最小值,在不考虑解析解的情况下,也可以利用类似的方法去求解。先随机找一个初始点x0x0x_0,然后求出该点的梯度,利用公式x1=x0−lr∗∇f(x)x1=x0−lr∗∇f(x)x_1=x_0-lr*\nabla f(x)模拟小球的滚动,其中lrlrlr为滚动的步长,也称为学习率。
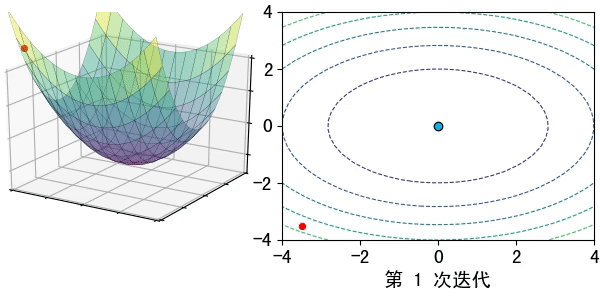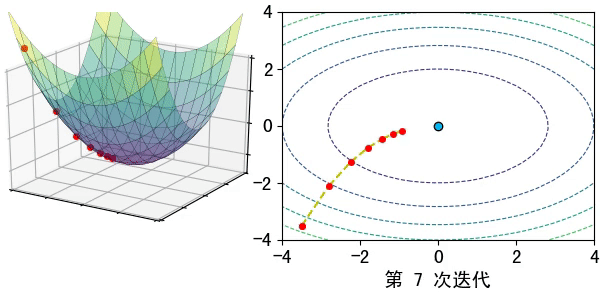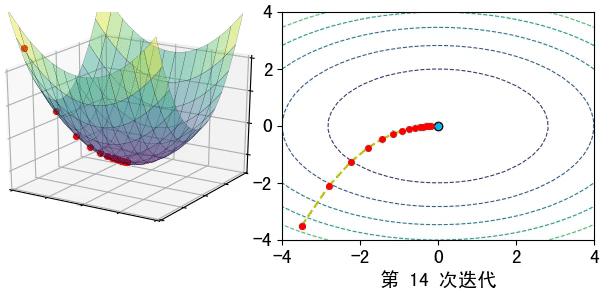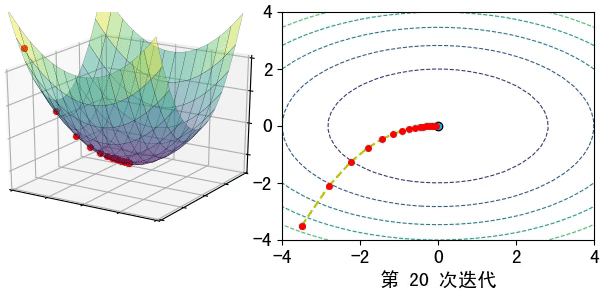
通过迭代公式 xn=xn−1−lr∗∇f(x)xn=xn−1−lr∗∇f(x)x_n=x_{n-1}-lr* \nabla f(x)一步步去逼近函数的极小值点。通常迭代的结束条件有:
- 指定迭代次数
- 计算迭代前后函数值的差距,若在一个非常小的阈值以为就可以认为已经找到最小值
4. 代码实现
案例 :f(x)=(x1−2)2+(x2−3)2+(x3−4)4f(x)=(x1−2)2+(x2−3)2+(x3−4)4f(x)=(x_1-2)^2+(x_2-3)^2+(x_3-4)^4
import numpy as np
#定义函数
def func(x):
return (x[0]-2)**2+(x[1]-3)**2+(x[2]-4)**2
#定义梯度
def gradFunc(x):
return np.array([(x[0]-2)*2,(x[1]-3)*2,(x[2]-4)*2])
# 定义梯度下降法
def SGD(init_x,func,gradFunc,lr=0.01,maxIter=100000,error=1e-10):
x=init_x
for iter in range(0,maxIter):
gd=gradFunc(x)
x_new=x-lr*gd
if(np.abs(func(x)-func(x_new))<error):
return x_new
x=x_new
return x_new
SGD(np.array([1,1,1]),func,gradFunc)
array([1.99998703, 2.99997406, 3.99996109])
SGD(np.array([10,10,10]),func,gradFunc)
array([2.00003215, 3.00002813, 4.00002411])