Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475
​ ​ ​ 线性模型最简单的形式就是输入变量的线性模型，但是，将一组输入变量的非线性函数进行线性组合，我们可以得到一类更加有用的函数，本章我们的讨论重点就是输入变量的非线性函数的线性组合。

1 线性基函数

​ ​ ​ 回归问题最简单的形式就是输入变量的线性函数，即

y(x,w)=w0+w1x1+w2x2+⋯+wDxDy(x,w)=w0+w1x1+w2x2+⋯+wDxDy(\mathbf x,\mathbf w)=w_0+w_1x_1+w_2x_2+\cdots+w_Dx_D
这称为线性回归（linear regression），更一般地

y(x,w)=w0+∑j=1M−1wjϕj(x)y(x,w)=w0+∑j=1M−1wjϕj(x)y(\mathbf x,\mathbf w)=w_0+\sum_{j=1}^{M-1}w_j\phi_j(\mathbf x)
其中ϕj(x)ϕj(x)\phi_j(\mathbf x)称为基函数（basis function），这是线性模型更一般的形式，具有更广泛的应用。参数w0w0w_0使数据中可以存在任意的偏置，故这个值通常称为偏置参数（bias parameter）。通常我们会定义ϕ0(x)=1ϕ0(x)=1\phi_0(\mathbf x)=1，那么此时

y(x,w)=∑j=0M−1wjϕj(x)=wTϕϕ(x)y(x,w)=∑j=0M−1wjϕj(x)=wTϕϕ(x)y(\mathbf x,\mathbf w)=\sum_{j=0}^{M-1}w_j\phi_j(\mathbf x)=\mathbf w^T\pmb\phi(\mathbf x)
其中w=(w0,⋯,wM−1)Tw=(w0,⋯,wM−1)T\mathbf w=(w_0,\cdots,w_{M-1})^T，ϕϕ(x)=(ϕ0(x),⋯,ϕM−1(x))Tϕϕ(x)=(ϕ0(x),⋯,ϕM−1(x))T\pmb\phi(\mathbf x)=(\phi_0(\mathbf x),\cdots,\phi_{M-1}(\mathbf x))^T。

​ ​ ​ 在PRML 基础知识一节中，我们曾经介绍过Polynomial Curve Fitting问题，那时的基函数即为ϕj(x)=xjϕj(x)=xj\phi_j(x)=x^j，这属于多项式基函数，多项基函数在许多场合很有用，但是它的一个局限性在于：它们是输入变量的全局函数，因此输入空间中一个区域的改变会影响到所有其他区域，比如，在顺序学习过程中，当我们有一个新得到的数据点，那么原则上我们只需要修改与之相近的区域，但是在多项式基函数的例子中，新得到一个数据点将会影响到所有区域。另外，如果我们要建立的模型是分段的，那么多项式基函数就有很大的局限性。对于此处出现的问题，我们可以这样解决：把输入空间切分为多个小区域，并对每个小区域用不同的多项式函数拟合。这样的函数叫做样条函数（spline function）。

​ ​ ​ 对于基函数还有其他选择，例如高斯基函数

ϕj(x)=exp{−(x−μj)22s2}ϕj(x)=exp{−(x−μj)22s2}\phi_j(x)=\text{exp}{-\frac{(x-\mu_j)^2}{2s^2}}
其中μjμj\mu_j控制了基函数在输入空间的位置，参数sss控制了基函数的空间大小。注意，虽然此种基函数称为高斯基函数，但是它未必是一个归一化的概率表达式，其归一化系数并不重要，因为它将与一个调节参数wjwjw_j相乘。另一种基函数的例子是sigmoid基函数，即

ϕj(x)=σ(x−μjs)ϕj(x)=σ(x−μjs)\phi_j(x)=\sigma(\frac{x-\mu_j}{s})
其中σ(x)=11+exp(−x)' role="presentation">σ(x)=11+exp(−x)σ(x)=11+exp(−x)\sigma(x)=\frac{1}{1+\text{exp}(-x)}，该函数是S函数（sigmoid function）的一个简单例子。因为我们已经证明S函数的另一个实例双曲正切（hyperbolic tangent）函数等价于logistic sigmoid函数的平移和缩放，即tanh(x)=2σ(2x)−1tanh⁡(x)=2σ(2x)−1\tanh(x)=2\sigma(2x)-1，所以我们也可以选择双曲正切函数作为基函数。下图展示了上述三个基函数的直观图像，从左至右依次为：多项式基函数、高斯基函数、sigmoid基函数

​ ​ ​ 基函数的选择实际上就是为了描述一个函数空间，根据所学知识，傅里叶（Fourier）函数可以描述任意的函数，因此，傅里叶基函数可以被选为基函数，这在信号处理领域是尤其重要的，这种研究产生了一类被称为小波（wavelet）的函数，为了简化应用，这些基函数被选为正交的。

​ ​ ​ 在本章中，我们通常不会关注基函数的具体形式，除非特别说明。

1.1 极大似然与最小平方

​ ​ ​ 对于一般的问题而言，极大似然方法与最小误差方法都是可行的思路，特别地，对于Polynomial Curve Fitting问题来说，就是极大似然与最小平方，现在来详细地讨论最小平方的方法与极大似然方法之间的关系。

​ ​ ​ 假设目标变量ttt由两部分组成：模型y(x,w)y(x,w)y(\mathbf x,\mathbf w)和噪声ϵϵ\epsilon组成，其中噪声ϵϵ\epsilon符合高斯分布（均值为零，精度为ββ\beta），即

t=y(x,w)+ϵt=y(x,w)+ϵt=y(\mathbf x,\mathbf w)+\epsilon
则有

p(t|x,w,β)=N(t|y(x,w),β−1)p(t|x,w,β)=N(t|y(x,w),β−1)p(t|\mathbf x,\mathbf w,\beta)=\mathcal N(t|y(\mathbf x,\mathbf w),\beta^{-1})
从PRML 基础知识5.2小节中知道，当我们新输入一个xx\mathbf x的时候，为使平方损失函数最小，目标变量ttt​的预测值应为

E(t|x)=∫tp(t|x)dt=y(x,w)E(t|x)=∫tp(t|x)dt=y(x,w)E(t|\mathbf x)=\int tp(t|\mathbf x)dt=y(\mathbf x,\mathbf w)
注意，噪声的假设说明，给定xxx的条件下，ttt的条件分布是单峰的，这对于⼀些实际应用来说是不合适的，后面一些章节将扩展到条件高斯分布的混合，那种情况下可以描述多峰的条件分布。

​ ​ ​ 现在考虑一个输入数据集X={x1⋯,xN}X={x1⋯,xN}\mathbf X={\mathbf x_1\cdots,\mathbf x_N}和对应的目标值t={t1,⋯,tN}t={t1,⋯,tN}\mathbf t={t_1,\cdots,t_N}，于是有如下的似然函数

p(t|X,w,β)=∏n=1NN(tn|wTϕϕ(xn),β−1)p(t|X,w,β)=∏n=1NN(tn|wTϕϕ(xn),β−1)p(\mathbf t|\mathbf X,\mathbf w,\beta)=\prod_{n=1}^N\mathcal N(t_n|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1})
在有监督学习（例如回归问题和分类问题）领域内，我们不是在寻找模型来对输入变量进行概率分布建模，因此xx\mathbf x总会出现在条件变量的位置上，因此此后不再在诸如p(t|x,w,β)p(t|x,w,β)p(\mathbf t|\mathbf x,\mathbf w,\beta)这类表达式中显式地写出xx\mathbf x。对上述似然函数取对数，得到

lnp(t|w,β)=∑n=1NlnN(tn|wTϕϕ(xn),β−1)=∑n=1Nln(1(2πβ−1)1/2exp{−(xn−wTϕϕ(xn))22β−1})=N2lnβ−N2ln(2π)−βED(w)ln⁡p(t|w,β)=∑n=1Nln⁡N(tn|wTϕϕ(xn),β−1)=∑n=1Nln⁡(1(2πβ−1)1/2exp{−(xn−wTϕϕ(xn))22β−1})=N2ln⁡β−N2ln⁡(2π)−βED(w)\begin{aligned}
\ln p(\mathbf t|\mathbf w,\beta)&=\sum_{n=1}^N\ln\mathcal N(t_n|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1})\
&=\sum_{n=1}^N\ln(\frac{1}{(2\pi\beta^{-1})^{1/2}}\text{exp}{-\frac{(\mathbf x_n-\mathbf w^T\pmb\phi(\mathbf x_n))^2}{2\beta^{-1}}})\
&=\frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)-\beta E_D(\mathbf w)
\end{aligned}
其中平方误差和函数为

ED(w)=12∑n=1N{tn−wTϕϕ(xn)}2ED(w)=12∑n=1N{tn−wTϕϕ(xn)}2E_D(\mathbf w)=\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2
这样，我们就得到了一个重要的结论：当噪声符合高斯分布时，极大似然方法等价于最小化平方和误差函数方法，特别地，当我们添加一个惩罚项（以保证不会过拟合）的时候，该结论仍然成立，这在PRML 基础知识的2.3小节中出现过。下面用极大似然方法确定参数ww\mathbf w和ββ\beta，上述对数似然函数对ww\mathbf w求偏导得到

∇lnp(t|w,β)=β∑n=1N{tn−wTϕϕ(xn)}ϕϕ(xn)T=0∇ln⁡p(t|w,β)=β∑n=1N{tn−wTϕϕ(xn)}ϕϕ(xn)T=0\nabla\ln p(\mathbf t|\mathbf w,\beta)=\beta\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}\pmb\phi(\mathbf x_n)^T=0
解得

wML=(ΦTΦ)−1ΦTtwML=(ΦTΦ)−1ΦTt\mathbf w_{ML}=(\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^T\mathbf t
这被称为最小平方问题的规范方程（normal equation），其中ΦΦ\mathbf\Phi是一个N×MN×MN\times M的矩阵，被称为设计矩阵（design matrix）

Φ=⎛⎝⎜⎜⎜⎜ϕ0(x1)ϕ0(x2)⋮ϕ0(xN)ϕ1(x1)ϕ1(x2)⋮ϕ1(xN)⋯⋯⋯ϕM−1(x1)ϕM−1(x2)⋮ϕM−1(xN)⎞⎠⎟⎟⎟⎟Φ=(ϕ0(x1)ϕ1(x1)⋯ϕM−1(x1)ϕ0(x2)ϕ1(x2)⋯ϕM−1(x2)⋮⋮⋮ϕ0(xN)ϕ1(xN)⋯ϕM−1(xN))\mathbf\Phi=
\left(
\begin{array}
{cccc}
\phi_0(\mathbf x_1) & \phi_1(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_1)\
\phi_0(\mathbf x_2) & \phi_1(\mathbf x_2) & \cdots & \phi_{M-1}(\mathbf x_2)\
\vdots & \vdots & & \vdots\
\phi_0(\mathbf x_N) & \phi_1(\mathbf x_N) & \cdots & \phi_{M-1}(\mathbf x_N)
\end{array}
\right)
现令Φ†=(ΦTΦ)−1ΦTΦ†=(ΦTΦ)−1ΦT\mathbf\Phi^{\dagger}=(\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^T，称为矩阵ΦΦ\mathbf\Phi的Moore-Penrose伪逆矩阵（pseudo-inverse matrix），可以视为逆矩阵概念对于非方阵的推广，如果矩阵ΦΦ\mathbf\Phi是方阵且可逆，那么有Φ−1=Φ†Φ−1=Φ†\mathbf\Phi^{-1}=\mathbf\Phi^{\dagger}。另外，当ΦTΦΦTΦ\mathbf\Phi^T\mathbf\Phi接近奇异矩阵时，直接求解规范方程会导致数值计算上的困难，此时可以通过奇异值分解（singular value decomposition or SVD）的方法解决。注意， 正则项的添加确保了矩阵是非奇异的。

​ ​ ​ 对于偏置参数w0w0w_0，如果我们显式地写出它，那么误差函数变为

ED(w)=12∑n=1N{tn−w0−∑j=1M−1wjϕj(xn)}2ED(w)=12∑n=1N{tn−w0−∑j=1M−1wjϕj(xn)}2E_D(\mathbf w)=\frac12\sum_{n=1}^N{t_n-w_0-\sum_{j=1}^{M-1}w_j\phi_j(\mathbf x_n)}^2
令其关于w0w0w_0的导数为零，解得

w0=t¯−∑j=1M−1wjϕj¯,t¯=1N∑n=1Ntn,ϕj¯=1N∑n=1Nϕj(xn)w0=t¯−∑j=1M−1wjϕj¯,t¯=1N∑n=1Ntn,ϕj¯=1N∑n=1Nϕj(xn)w_0=\bar{t}-\sum_{j=1}^{M-1}w_j\bar{\phi_j},
\quad\bar{t}=\frac1N\sum_{n=1}^Nt_n,
\quad\bar{\phi_j}=\frac1N\sum_{n=1}^N\phi_j(\mathbf x_n)
因此w0w0w_0的作用就是补偿了目标值的平均值与基函数的值的平均值的加权求和之间的差。

​ ​ ​ 类似地，上述对数似然函数对ββ\beta求偏导得到

∇lnp(t|w,β)=N2β−12∑n=1N{tn−wTϕϕ(xn)}2=0∇ln⁡p(t|w,β)=N2β−12∑n=1N{tn−wTϕϕ(xn)}2=0\nabla\ln p(\mathbf t|\mathbf w,\beta)=\frac{N}{2\beta}-\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2=0
解得

1βML=1N∑n=1N{tn−wTMLϕϕ(xn)}21βML=1N∑n=1N{tn−wMLTϕϕ(xn)}2\frac{1}{\beta_{ML}}=\frac1N\sum_{n=1}^N{t_n-\mathbf w_{ML}^T\pmb\phi(\mathbf x_n)}^2
因此我们看到噪声精度的倒数由目标值在回归函数周围的残留方差（residual variance）给出。

3.2 顺序学习

​ ​ ​ 顺序学习在数据集非常大或者数据点依次到达的情况下非常有用，一个常用的方法是随机梯度下降（stochastic gradient descent）或者称为顺序梯度下降（sequential gradient descent）

w(τ+1)=w(τ)−η∇Enw(τ+1)=w(τ)−η∇En\mathbf w^{(\tau+1)}=\mathbf w^{(\tau)}-\eta\nabla E_n
其中ττ\tau表示迭代次数，ηη\eta是学习率参数，EnEnE_n表示误差函数，对于平方和误差函数而言

w(τ+1)=w(τ)+η(tn−w(τ)Tϕϕ(xn))ϕϕ(xn)w(τ+1)=w(τ)+η(tn−w(τ)Tϕϕ(xn))ϕϕ(xn)\mathbf w^{(\tau+1)}=\mathbf w^{(\tau)}+\eta(t_n-\mathbf {w^{(\tau)}}^T\pmb\phi(\mathbf x_n))\pmb\phi(\mathbf x_n)
这和PRML 概率分布中3.9小节介绍的Robbins-Monro方法有相通的地方，该方法称为最小均方（least-mean-squares or LMS）算法，其中ηη\eta的值需要仔细选取以保证收敛。

3.3 正则化最小平方

​ ​ ​ 向误差函数中添加正则项，总误差函数变成了

12∑n=1N{tn−wTϕϕ(xn)}2+λ2wTw12∑n=1N{tn−wTϕϕ(xn)}2+λ2wTw\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2+\frac\lambda2\mathbf w^T\mathbf w
并给出如下定义

ED(w)EW(w)=12∑n=1N{tn−wTϕϕ(xn)}2=12wTwED(w)=12∑n=1N{tn−wTϕϕ(xn)}2EW(w)=12wTw\begin{aligned}
E_D(\mathbf w)&=\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2\
E_W(\mathbf w)&=\frac12\mathbf w^T\mathbf w
\end{aligned}
则可记总误差函数为ED(w)+λEW(w)ED(w)+λEW(w)E_D(\mathbf w)+\lambda E_W(\mathbf w)。注意，正则化项并不是唯一的，但其中最简单的形式就是λ2wTwλ2wTw\frac\lambda2\mathbf w^T\mathbf w。这种对于正则化项的选择方法在机器学习文献中称为权值衰减（weight decay），因为在顺序学习中，它倾向于让权值向零的方向衰减，除非有数据支持；在统计学中，它提供了一个参数收缩（parameter shrinkage）的例子，因为这种方法把参数的值向零的方向收缩。将上述总误差函数对ww\mathbf w​求偏导并令其为零，解得

w=(λI+ΦTΦ)−1ΦTtw=(λI+ΦTΦ)−1ΦTt\mathbf w=(\lambda\mathbf I+\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^T\mathbf t
这是wML=(ΦTΦ)−1ΦTtwML=(ΦTΦ)−1ΦTt\mathbf w_{ML}=(\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^T\mathbf t的一个扩展。

​ ​ ​ 正则化项可以选取其他形式，更一般地，总误差函数为

12∑n=1N{tn−wTϕϕ(xn)}2+λ2∑j=1M|wj|q12∑n=1N{tn−wTϕϕ(xn)}2+λ2∑j=1M|wj|q\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2+\frac\lambda2\sum_{j=1}^M|w_j|^q
其中q=1q=1q=1的情形称为套索（lasso），它的性质是：如果λλ\lambda合理地大，那么某些系数wjwjw_j将会等于零，从而产生了一个稀疏（sparse）模型。我们注意到最小化上述的总误差函数等价于在∑Mj=1|wj|q≤η∑j=1M|wj|q≤η\sum_{j=1}^M|w_j|^q\leq\eta（其中ηη\eta是选取的合适的值）的条件下将12∑Nn=1{tn−wTϕϕ(xn)}212∑n=1N{tn−wTϕϕ(xn)}2\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2进行最小化，不妨令∑Mj=1|wj|q=η∑j=1M|wj|q=η\sum_{j=1}^M|w_j|^q=\eta，那么这通过拉格朗日乘数法很容易求解。下面两幅图说明了q=1q=1q=1时稀疏性的来源

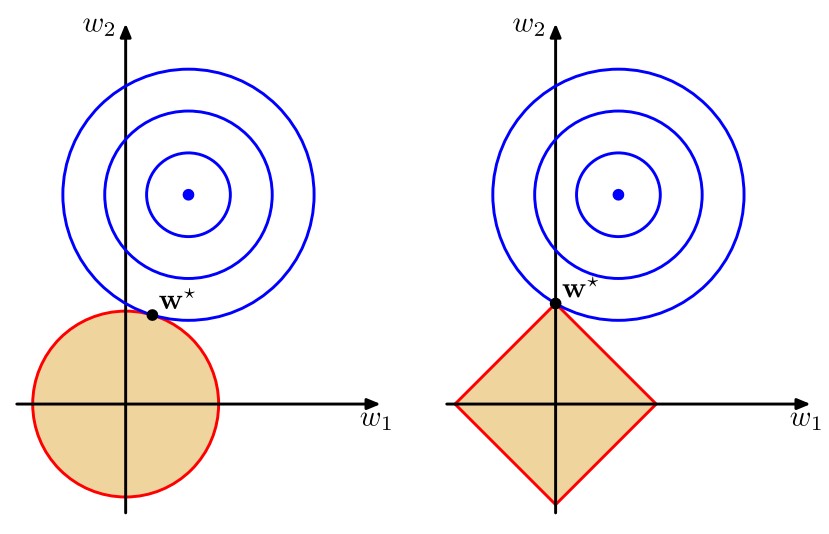
第一幅图给出了不同的qqq值对应的正则项的轮廓线，第二幅图中蓝色同心圆即为12∑Nn=1{tn−wTϕϕ(xn)}212∑n=1N{tn−wTϕϕ(xn)}2\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2等于不同值对应的图像，因此该图明确说明了当q=1q=1q=1时，解得的w∗w∗\mathbf w^*将会有某个wjwjw_j的数值为零。

3.4 多个目标变量

​ ​ ​ 在实际应用中，我们可能想要预测K>1K>1K>1个变量，此时记要预测的目标变量为t=(t1,⋯,tK)Tt=(t1,⋯,tK)T\mathbf t=(t_1,\cdots,t_K)^T，那么有两个思路处理此问题：一是对每个目标变量单独建模处理，二是引入一个整体的函数进行建模，即

y(x,w)=WTϕϕ(x)y(x,w)=WTϕϕ(x)\mathbf y(\mathbf x,\mathbf w)=\mathbf W^T\pmb\phi(\mathbf x)
其中y(x,w)y(x,w)\mathbf y(\mathbf x,\mathbf w)是一个KKK维列向量，WW\mathbf W是一个M×KM×KM\times K的参数矩阵，ϕϕ(x)ϕϕ(x)\pmb\phi(\mathbf x)是一个MMM维列向量，每个元素为ϕj(x)ϕj(x)\phi_j(\mathbf x)，并且ϕ0(x)=1ϕ0(x)=1\phi_0(\mathbf x)=1。如果我们令目标向量的条件概率分布是一个各向同性的高斯分布，则

p(t|x,W,β)=N(t|WTϕϕ(x),β−1I)p(t|x,W,β)=N(t|WTϕϕ(x),β−1I)p(\mathbf t|\mathbf x,\mathbf W,\beta)=\mathcal N(\mathbf t|\mathbf W^T\pmb\phi(\mathbf x),\beta^{-1}\mathbf I)
如果我们有观测数据集T=(tT1,⋯,tTN)TT=(t1T,⋯,tNT)T\mathbf T=(\mathbf t_1^T,\cdots,\mathbf t_N^T)^T，即该矩阵大小为N×KN×KN\times K，其中第nnn行为tTntnT\mathbf t_n^T，并将输入向量类似地组合成X=(xT1,⋯,xTN)TX=(x1T,⋯,xNT)T\mathbf X=(\mathbf x_1^T,\cdots,\mathbf x_N^T)^T，那么对数似然函数为

lnp(T|X,W,β)=∑n=1NlnN(tn|WTϕϕ(xn),β−1I)=NK2ln(β2π)−β2∑n=1N||tn−WTϕϕ(xn)||2ln⁡p(T|X,W,β)=∑n=1Nln⁡N(tn|WTϕϕ(xn),β−1I)=NK2ln⁡(β2π)−β2∑n=1N||tn−WTϕϕ(xn)||2\begin{aligned}
\ln p(\mathbf T|\mathbf X,\mathbf W,\beta)&=\sum_{n=1}^N\ln\mathcal N(\mathbf t_n|\mathbf W^T\pmb\phi(\mathbf x_n),\beta^{-1}\mathbf I)\
&=\frac{NK}{2}\ln(\frac{\beta}{2\pi})-\frac\beta2\sum_{n=1}^N||\mathbf t_n-\mathbf W^T\pmb\phi(\mathbf x_n)||^2
\end{aligned}
类似地可解出

WML=(ΦTΦ)−1ΦTTWML=(ΦTΦ)−1ΦTT\mathbf W_{ML}=(\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^TT
该结果可以分解为

wk=(ΦTΦ)−1ΦTtk=Φ†tkwk=(ΦTΦ)−1ΦTtk=Φ†tk\mathbf w_k=(\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^T\mathbf t_k=\mathbf\Phi^{\dagger}\mathbf t_k
因此不同的目标变量实际上是可以被分解出来的，伪逆矩阵Φ†Φ†\mathbf\Phi^{\dagger}是被所有目标变量所共享的，所以，单一目标变量的情形很容易扩展到多变量的情形。

2 偏置-方差分解

​ ​ ​ 频率主义和贝叶斯主义看待模型复杂度的思路是不同的，本小节介绍频率主义思路——偏置-方差分解。在PRML 基础知识中5.2节中我们已经说明了平方损失函数的期望可以写成（记h(x)=Et(t|x)h(x)=Et(t|x)h(\mathbf x)=E_t(t|\mathbf x)）

E(L)=∫(y(x)−h(x))2p(x)dx+∫var(t|x)p(x)dxE(L)=∫(y(x)−h(x))2p(x)dx+∫var(t|x)p(x)dxE(L)=\int(y(\mathbf x)−h(\mathbf x))^2p(\mathbf x)d\mathbf x+\int\text{var}(t|\mathbf x)p(\mathbf x)d\mathbf x
其中与y(x)y(x)y(\mathbf x)无关的第二项是由数据的噪声造成的（如果噪声为零，那么var(t|x)=0var(t|x)=0\text{var}(t|\mathbf x)=0）。显然，如果我们有足够多的数据点，那么就能在很高的精度上建模得到h(x)h(x)h(\mathbf x)与y(x)y(x)y(\mathbf x)很接近。

​ ​ ​ 如果我们使用由参数向量ww\mathbf w控制的函数y(x,w)y(x,w)y(\mathbf x,\mathbf w)对h(x)h(x)h(\mathbf x)建模，那么从贝叶斯主义的观点来看，模型的不确定性是通过ww\mathbf w的后验概率分布来表示的。但是，频率主义方法涉及到根据数据集DDD对ww\mathbf w进行点估计，然后试着通过下面的思想实验来表示估计的不确定性。假设我们有许多数据集，每个数据集的大小为NNN，并且每个数据集都独立地从分布p(t,x)p(t,x)p(t,\mathbf x)中抽取。对于任意给定的数据集DDD，我们可以运行我们的学习算法，得到⼀个预测函数y(x;D)y(x;D)y(\mathbf x;D)。不同的数据集会给出不同的函数，从而给出不同的平方损失的值。这样，特定的学习算法的表现就可以通过取各个数据集上的表现的平均值来进行评估。

​ ​ ​ 对一个特定的数据集DDD而言，E(L)E(L)E(L)表达式的第一项为

{y(x;D)−h(x)}2={y(x;D)−ED(y(x;D))+ED(y(x;D))−h(x)}2={y(x;D)−ED(y(x;D))}2+{ED(y(x;D))−h(x)}2+2{y(x;D)−ED(y(x;D))}⋅{ED(y(x;D))−h(x)}{y(x;D)−h(x)}2={y(x;D)−ED(y(x;D))+ED(y(x;D))−h(x)}2={y(x;D)−ED(y(x;D))}2+{ED(y(x;D))−h(x)}2+2{y(x;D)−ED(y(x;D))}⋅{ED(y(x;D))−h(x)}\begin{aligned}
{y(\mathbf x;D)-h(\mathbf x)}^2&={y(\mathbf x;D)-E_D(y(\mathbf x;D))+E_D(y(\mathbf x;D))-h(\mathbf x)}^2\
&={y(\mathbf x;D)-E_D(y(\mathbf x;D))}^2+{E_D(y(\mathbf x;D))-h(\mathbf x)}^2\
&\quad+2{y(\mathbf x;D)-E_D(y(\mathbf x;D))}\cdot{E_D(y(\mathbf x;D))-h(\mathbf x)}
\end{aligned}
现在在两侧对DDD求期望，得到

ED({y(x;D)−h(x)}2)={ED(y(x;D))−h(x)}2+ED({y(x;D)−ED(y(x;D))}2)=偏置2+方差ED({y(x;D)−h(x)}2)={ED(y(x;D))−h(x)}2+ED({y(x;D)−ED(y(x;D))}2)=偏置2+方差\begin{aligned}
E_D({y(\mathbf x;D)-h(\mathbf x)}^2)&={E_D(y(\mathbf x;D))-h(\mathbf x)}^2+E_D({y(\mathbf x;D)-E_D(y(\mathbf x;D))}^2)\
&=\text{偏置}^2+\text{方差}
\end{aligned}
其中第一项称为平方偏置（bias），表示所有数据集的平均预测与预期的回归函数之间的差异；第二项称为方差（variance），度量了对于单独的数据集，模型给出的解在平均值附近的波动情况，因此也度量了函数y(x;D)y(x;D)y(\mathbf x;D)对于特定的数据集的敏感程度。现在，我们的平方损失函数就可以分解为

E(L)=期望损失=偏置2+方差+噪声E(L)=期望损失=偏置2+方差+噪声E(L)=\text{期望损失}=\text{偏置}^2+\text{方差}+\text{噪声}
其中

偏置2方差噪声=∫{ED(y(x;D))−h(x)}2p(x)dx=∫ED({y(x;D)−ED(y(x;D))}2)dx=∬{h(x)−t}2p(x,t)dxdt=∫var(t|x)p(x)dx偏置2=∫{ED(y(x;D))−h(x)}2p(x)dx方差=∫ED({y(x;D)−ED(y(x;D))}2)dx噪声=∬{h(x)−t}2p(x,t)dxdt=∫var(t|x)p(x)dx\begin{aligned}
\text{偏置}^2&=\int{E_D(y(\mathbf x;D))-h(\mathbf x)}^2p(\mathbf x)d\mathbf x\
\text{方差}&=\int E_D({y(\mathbf x;D)-E_D(y(\mathbf x;D))}^2)d\mathbf x\
\text{噪声}&=\iint{h(\mathbf x)-t}^2p(\mathbf x,t)d\mathbf xdt=\int\text{var}(t|\mathbf x)p(\mathbf x)d\mathbf x
\end{aligned}
现在，偏置和方差是指积分后的量。

​ ​ ​ 我们的目标是最小化期望损失，它可以分解为（平方）偏置、方差和⼀个常数噪声项的和。对于非常灵活的模型来说， 偏置较小，方差较大。对于相对固定的模型来说，偏置较大，方差较小。有着最优预测能力的模型是在偏置和方差之间取得最优的平衡的模型。下图以正弦分布为例说明了这一点

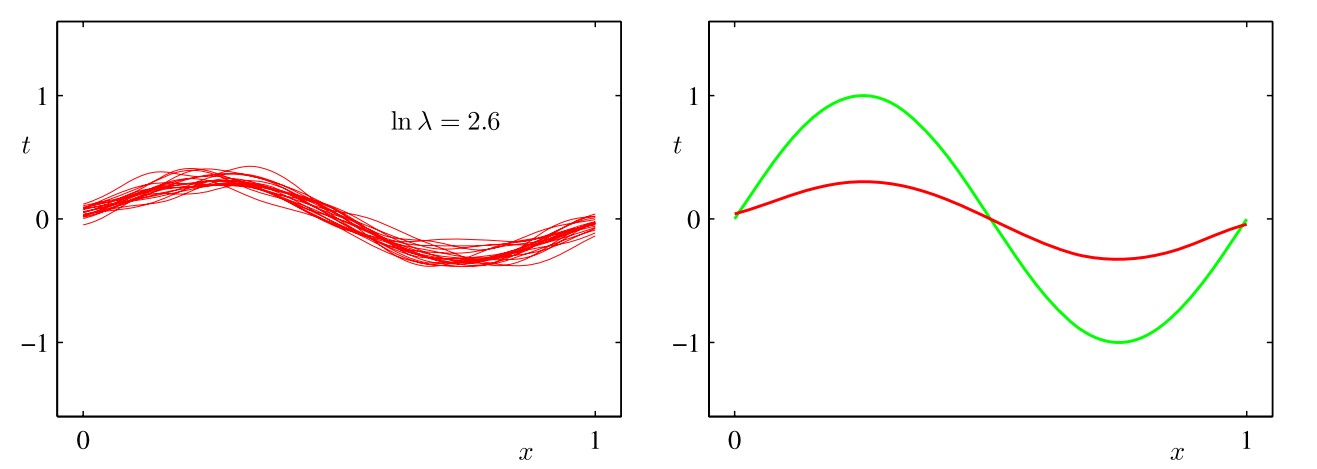
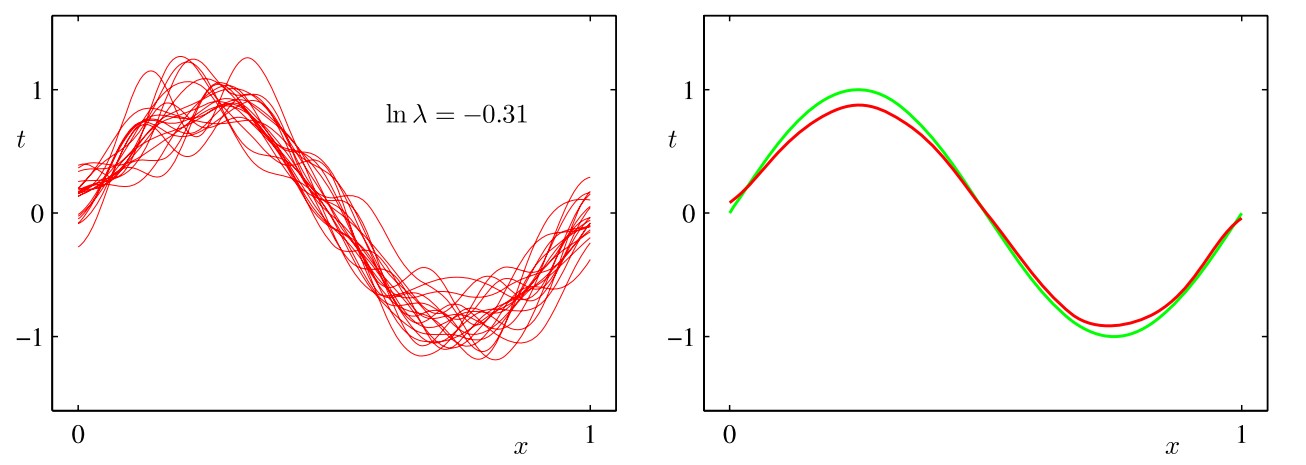
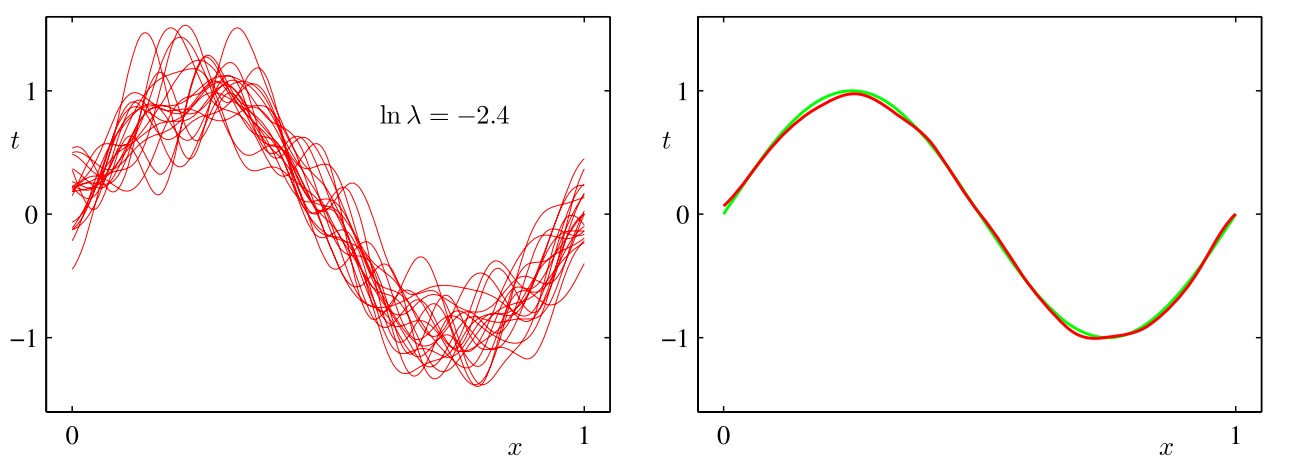
我们预先生成了符合正弦分布的若干组数据点，每个集合都包含NNN个数据点，数据集的编号为l=1,⋯,Ll=1,⋯,Ll=1,\cdots,L，并且对于每个数据集D(l)D(l)D(l)，通过最小化正则化的误差函数12∑Nn=1{tn−wTϕϕ(xn)}2+λ2wTw12∑n=1N{tn−wTϕϕ(xn)}2+λ2wTw\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2+\frac\lambda2\mathbf w^T\mathbf w拟合了⼀个带有若干个高斯基函数的模型，然后给出了预测函数y(l)(x)y(l)(x)y^{(l)}(x)，如上图所示（左侧的红色曲线表示各数据集的拟合结果，右侧的红色曲线表示左侧红色曲线的平均）。第一行对应着较大的正则化系数λλ\lambda，这样的模型的方差很小（因为左侧图中的红色曲线看起来很相似），但是偏置很大（因为右侧图中的两条曲线看起来相当不同）。相反，在最后一行，正则化系数λλ\lambda很小，这样模型的方差较大（因为左侧图中的红色曲线变化性相当大），但是偏置很小（因为平均拟合的结果与原始正弦曲线十分吻合）。从上面的内容可以直观看出，求（加权）平均是得到较为准确的模型的重要手法，这不仅在频率主义方法中起作用（此时将多个数据集得到的拟合函数求（加权）平均），而且在贝叶斯主义方法中仍然起作用（此时将多个后验概率所支持的参数进行（加权）平均）。

​ ​ ​ 下面我们仍以正弦分布为例定量分析方差-偏置中的合理平衡。平均预测为

y¯(x)=1L∑l=1Ly(l)(x)y¯(x)=1L∑l=1Ly(l)(x)\bar{y}(x)=\frac1L\sum_{l=1}^Ly^{(l)}(x)
并且积分后的平方偏置以及积分后的方差为

偏置2方差=1N∑n=1N{y¯(xn)−h(xn)}2=1N∑n=1N1L∑l=1L{y(l)(xn)−y¯(xn)}2偏置2=1N∑n=1N{y¯(xn)−h(xn)}2方差=1N∑n=1N1L∑l=1L{y(l)(xn)−y¯(xn)}2\begin{aligned}
\text{偏置}^2&=\frac1N\sum_{n=1}^N{\bar{y}(x_n)-h(x_n)}^2\
\text{方差}&=\frac1N\sum_{n=1}^N\frac1L\sum_{l=1}^L{y^{(l)}(x_n)-\bar{y}(x_n)}^2
\end{aligned}
下图直观展示了不同的λλ\lambda对应的偏置和方差以及它们的加和

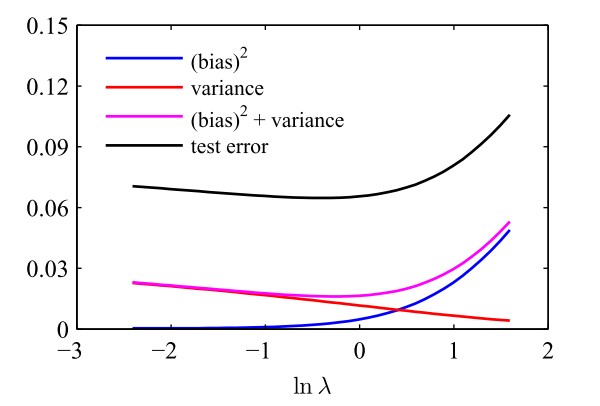
明显可以看出：当λλ\lambda较小时，惩罚项的重要程度较低，此时模型倾向于过拟合（即对噪声过于重视），因此偏置较小但方差较大；当λλ\lambda较大时，惩罚项的重要程度较高，此时模型容易拟合不足，因此偏置较大但方差较小。只有λλ\lambda适中时，才能取到偏置2+方差偏置2+方差\text{偏置}^2+\text{方差}的最小值。

​ ​ ​ 虽然偏置-方差分解能够从频率主义的角度对模型的复杂度提供思路，但是它的实用价值很有限。这是因为偏置-方差分解依赖于对所有的数据集求平均，而在实际应用中我们常常只有⼀个观测数据集。另外，如果我们有大量的已知规模的独立的训练数据集，那么把它们组合成一个更大的训练数据集显然会降低给定复杂度的模型的过拟合程度，这个思路比求平均更加有用。 由于有这么多局限性，因此我们在下⼀节将讨论线性基函数模型的贝叶斯观点。它不仅提供了对于过拟合现象的深刻认识，还提出了解决模型复杂度问题的实用的方法。

3 贝叶斯线性回归

​ ​ ​ 线性回归的贝叶斯方法避免了过拟合问题，并引出了使用数据本身确定模型复杂度的自动化方法。

3.1 参数分布

​ ​ ​ 在PRML 概率分布中的3.7节我们证明了，当有如下形式的边缘分布（先验概率）和条件高斯分布（似然函数）

p(x)p(y|x)=N(x|μμ,ΛΛ−1)=N(y|Ax+b,L−1)p(x)=N(x|μμ,ΛΛ−1)p(y|x)=N(y|Ax+b,L−1)\begin{aligned}
p(\mathbf x)&=\mathcal N(\mathbf x|\pmb\mu,\pmb\Lambda^{-1})\
p(\mathbf y|\mathbf x)&=\mathcal N(\mathbf y|\mathbf A\mathbf x+\mathbf b,\mathbf L^{-1})
\end{aligned}
的时候，可得

p(y)p(x|y)=N(y|Aμμ+b,L−1+AΛ−1AT)=N(x|Σ{ATL(y−b)+ΛΛμμ},Σ)p(y)=N(y|Aμμ+b,L−1+AΛ−1AT)p(x|y)=N(x|Σ{ATL(y−b)+ΛΛμμ},Σ)\begin{aligned}
p(\mathbf y)&=\mathcal N(\mathbf y|\mathbf A\pmb\mu+\mathbf b,\mathbf L^{-1}+\mathbf A\mathbf\Lambda^{-1}\mathbf A^T)\
p(\mathbf x|\mathbf y)&=\mathcal N(\mathbf x|\mathbf\Sigma{\mathbf A^T\mathbf L(\mathbf y-\mathbf b)+\pmb\Lambda\pmb\mu},\mathbf\Sigma)
\end{aligned}
其中Σ=(ΛΛ+ATLA)−1Σ=(ΛΛ+ATLA)−1\mathbf\Sigma=(\pmb\Lambda+\mathbf A^T\mathbf L\mathbf A)^{-1}。

​ ​ ​ 现在，似然函数p(t|w)p(t|w)p(\mathbf t|\mathbf w)为

p(t|w)=∏n=1NN(tn|wTϕϕ(xn),β−1I)∝N(t|Φw,β−1I)p(t|w)=∏n=1NN(tn|wTϕϕ(xn),β−1I)∝N(t|Φw,β−1I)p(\mathbf t|\mathbf w)=\prod_{n=1}^N\mathcal N(t_n|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1}\mathbf I)\varpropto\mathcal N(\mathbf t|\mathbf\Phi\mathbf w,\beta^{-1}\mathbf I)
为了保证共轭性，参数ww\mathbf w的先验分布可设为高斯分布

p(w)=N(w|m0,S0)p(w)=N(w|m0,S0)p(\mathbf w)=\mathcal N(\mathbf w|\mathbf m_0,\mathbf S_0)
其中m0m0\mathbf m_0为（先验的）均值，S0S0\mathbf S_0为（先验的）协方差。那么根据上面的结论，我们可以得到参数ww\mathbf w的后验分布为

p(w|t)=N(w|SN{βΦTt+S−10m0},SN)S−1N=S−10+βΦTΦp(w|t)=N(w|SN{βΦTt+S0−1m0},SN)SN−1=S0−1+βΦTΦp(\mathbf w|\mathbf t)=\mathcal N(\mathbf w|\mathbf S_N{\beta\mathbf\Phi^T\mathbf t+\mathbf S_0^{-1}\mathbf m_0},\mathbf S_N)\
\mathbf S_N^{-1}=\mathbf S_0^{-1}+\beta\mathbf\Phi^T\mathbf\Phi
如果我们令（先验的）协方差S0=α−1IS0=α−1I\mathbf S_0=\alpha^{-1}\mathbf I，其中α→0α→0\alpha\rightarrow0，那么在实际意义上就给定了一个无限宽的先验分布，相当于没有先验分布，此时的均值mN=(ΦTΦ)−1ΦTt=wMLmN=(ΦTΦ)−1ΦTt=wML\mathbf m_N=(\mathbf\Phi^T\mathbf\Phi)^{-1}\mathbf\Phi^T\mathbf t=\mathbf w_{ML}，这就是极大似然方法中的规范方程。在本章的剩余部分，为简便起见，我们假设先验分布p(w)p(w)p(\mathbf w)是各向同性的零均值高斯分布，即

p(w)=N(w|0,α−1I)p(w)=N(w|0,α−1I)p(\mathbf w)=\mathcal N(\mathbf w|\mathbf 0,\alpha^{-1}\mathbf I)
那么此时有

mNS−1N=βSNΦTt=αI+βΦTΦmN=βSNΦTtSN−1=αI+βΦTΦ\begin{aligned}
\mathbf m_N&=\beta\mathbf S_N\mathbf\Phi^T\mathbf t\
\mathbf S_N^{-1}&=\alpha\mathbf I+\beta\mathbf\Phi^T\mathbf\Phi
\end{aligned}
且后验概率的对数为

lnp(w|t)=−β2∑n=1N{tn−wTϕϕ(xn)}2−α2wTw+常数ln⁡p(w|t)=−β2∑n=1N{tn−wTϕϕ(xn)}2−α2wTw+常数\ln p(\mathbf w|\mathbf t)=-\frac\beta2\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2-\frac\alpha2\mathbf w^T\mathbf w+\text{常数}
这正好对应含正则化项的总误差函数12∑Nn=1{tn−wTϕϕ(xn)}2+λ2wTw12∑n=1N{tn−wTϕϕ(xn)}2+λ2wTw\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2+\frac\lambda2\mathbf w^T\mathbf w中令λ=αβλ=αβ\lambda=\frac\alpha\beta。需要注意的是，在贝叶斯线性回归中，我们没有引入任何“惩罚项”的概念，这就说明在贝叶斯线性回归中过拟合问题自动地被避免了。

​ ​ ​ 现在以直线拟合为例说明线性基函数的贝叶斯学习过程，以及后验概率分布的顺序更新过程。考虑单一输入变量xxx和单一目标变量ttt，以及线性模型y(x,w)=w0+w1xy(x,w)=w0+w1xy(x,\mathbf w)=w_0+w_1x。预先生成满足f(x,a)=a0+a1xf(x,a)=a0+a1xf(x,\mathbf a)=a_0+a_1x的一组点，其中a0=−0.3a0=−0.3a_0=−0.3且a1=0.5a1=0.5a_1=0.5，并增加⼀个标准差为0.20.20.2的高斯噪声，得到数据集（目标变量为ttt）。现在我们想从数据集中恢复出a0a0a_0和a1a1a_1的值，并且想研究模型对于数据集规模的依赖关系。我们假设噪声方差是已知的，因此我们把精度参数设置为它的真实值β=(10.2)2=25β=(10.2)2=25\beta=(\frac{1}{0.2})^2=25。类似地，我们令α=2.0α=2.0\alpha=2.0（稍后会简短讨论从训练集中确定αα\alpha和ββ\beta的值的策略）。下图给出了当数据集的规模增加时贝叶斯学习的结果，还直观展示了贝叶斯学习的顺序本质（即当新数据点到达时，后验分布变成了先验分布）

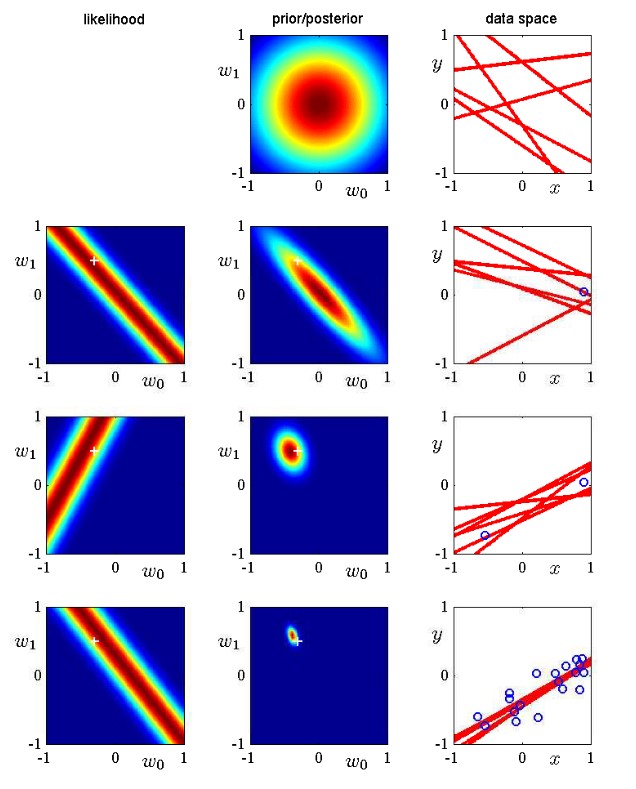
真实参数值a0=−0.3a0=−0.3a_0=−0.3以及a1=0.5a1=0.5a_1=0.5在上图中被标记为白色十字。第一行是开始训练之前的图像，即先验分布的图像，我们设参数w=(w0w1)w=(w0w1)\mathbf w=\left(\begin{array}{c}w_0\w_1\end{array}\right)先验分布为各向同性的零均值高斯分布p(w)=N(w|0,α−1I)p(w)=N(w|0,α−1I)p(\mathbf w)=\mathcal N(\mathbf w|\mathbf 0,\alpha^{-1}\mathbf I)，它的图像如第一行中间图所示，从中随机抽取六组先验参数ww\mathbf w，得到第一行右侧图中所示的六条红线。第二行中有一个数据点到达（右侧图中的蓝色圆圈），左侧图为该数据点的似然函数p(t|w)p(t|w)p(t|\mathbf w)的图像。如果我们把这个似然函数与第一行的先验概率相乘，然后归一化，我们就得到了第二行中间图给出的后验概率分布。继续从这个后验概率分布中抽取六组参数www，对应的回归函数y(x,w)y(x,w)y(x,\mathbf w)如第二行右侧图所示。注意，这些样本直线全部穿过数据点的附近位置（此处的“附近”由噪声精度ββ\beta确定）。上图第三行展示了第二个数据点到达后的效果。第四行展示了202020个数据点到达后的效果。左侧图展示了第202020个数据点自身的似然函数，中间图展示了融合了202020次观测信息的后验概率分布。注意与第三行相比，这个后验概率分布变得更加尖锐。在无穷多个数据点的极限情况下，后验概率分布会变成一个Delta函数，这个函数的中心就是用白色十字标记出的真实参数值。

​ ​ ​ 当然，除了高斯分布，先验分布p(w)p(w)p(\mathbf w)也可以取其他形式，比如高斯分布的推广形式

p(w|α)={q2(α2)1/q1Γ(1/q)}Mexp{−α2∑j=0M−1|wj|q}p(w|α)={q2(α2)1/q1Γ(1/q)}Mexp{−α2∑j=0M−1|wj|q}p(\mathbf w|\alpha)={\frac{q}{2}(\frac\alpha2)^{1/q}\frac{1}{\Gamma(1/q)}}^M\text{exp}{-\frac\alpha2\sum_{j=0}^{M-1}|w_j|^q}
其中α=2α=2\alpha=2对应高斯分布。

3.2 预测分布

​ ​ ​ 我们的预测值通常由一个分布来描述

p(t|t,α,β)=∫p(t|w)⋅p(w|t,α,β)dw=∫p(t|x,w,β)⋅p(w|t)dw=∫N(t|y(x,w),β−1)⋅N(w|SN{βΦTt+S−10m0},SN)dwp(t|t,α,β)=∫p(t|w)⋅p(w|t,α,β)dw=∫p(t|x,w,β)⋅p(w|t)dw=∫N(t|y(x,w),β−1)⋅N(w|SN{βΦTt+S0−1m0},SN)dw\begin{aligned}
p(t|\mathbf t,\alpha,\beta)&=\int p(t|\mathbf w)\cdot p(\mathbf w|\mathbf t,\alpha,\beta)d\mathbf w\
&=\int p(t|\mathbf x,\mathbf w,\beta)\cdot p(\mathbf w|\mathbf t)d\mathbf w\
&=\int\mathcal N(t|y(\mathbf x,\mathbf w),\beta^{-1})\cdot
\mathcal N(\mathbf w|\mathbf S_N{\beta\mathbf\Phi^T\mathbf t+\mathbf S_0^{-1}\mathbf m_0},\mathbf S_N)d\mathbf w
\end{aligned}
其中p(t|x,t,α,β)=N(t|mNTϕϕ(x),σN2(x))σN2(x)=1β+ϕϕ(x)TSNϕϕ(x)' role="presentation" style="position: relative;">p(t|x,t,α,β)=N(t|mTNϕϕ(x),σ2N(x))σ2N(x)=1β+ϕϕ(x)TSNϕϕ(x)p(t|x,t,α,β)=N(t|mNTϕϕ(x),σN2(x))σN2(x)=1β+ϕϕ(x)TSNϕϕ(x)

p(t|\mathbf x,\mathbf t,\alpha,\beta)=\mathcal N(t|\mathbf m_N^T\pmb\phi(\mathbf x),\sigma_N^2(\mathbf x))\
\sigma_N^2(\mathbf x)=\frac1\beta+\pmb\phi(\mathbf x)^T\mathbf S_N\pmb\phi(\mathbf x)
其中预测分布的方差σ2N(x)σN2(x)\sigma_N^2(\mathbf x)中的第一项表示数据的噪声，第二项反映了与参数ww\mathbf w相关联的不确定性。由于噪声和ww\mathbf w的分布是相互独立的高斯分布，因此它们的值是可以直接相加的。当新的数据点到达的时候，方差会缩小，因此可以证明σ2N+1(x)≤σ2N(x)σN+12(x)≤σN2(x)\sigma_{N+1}^2(\mathbf x)\leq\sigma_N^2(\mathbf x)，进而当N→∞N→∞N\rightarrow\infty时，第二项会趋于零，从而预测分布的方差只与参数ββ\beta控制的具有可加性的噪声有关。

​ ​ ​ 在前一小节我们以直线拟合为例介绍了线性基函数的贝叶斯学习过程，以及后验概率分布的顺序更新过程。现在，我们考虑一个更具体的例子——正弦分布，并以此为例说明贝叶斯线性回归模型的预测分布，其中基函数选为高斯基函数。在下图中，绿线表示正弦曲线，生成的数据以此为基础并附加一定的高斯噪声

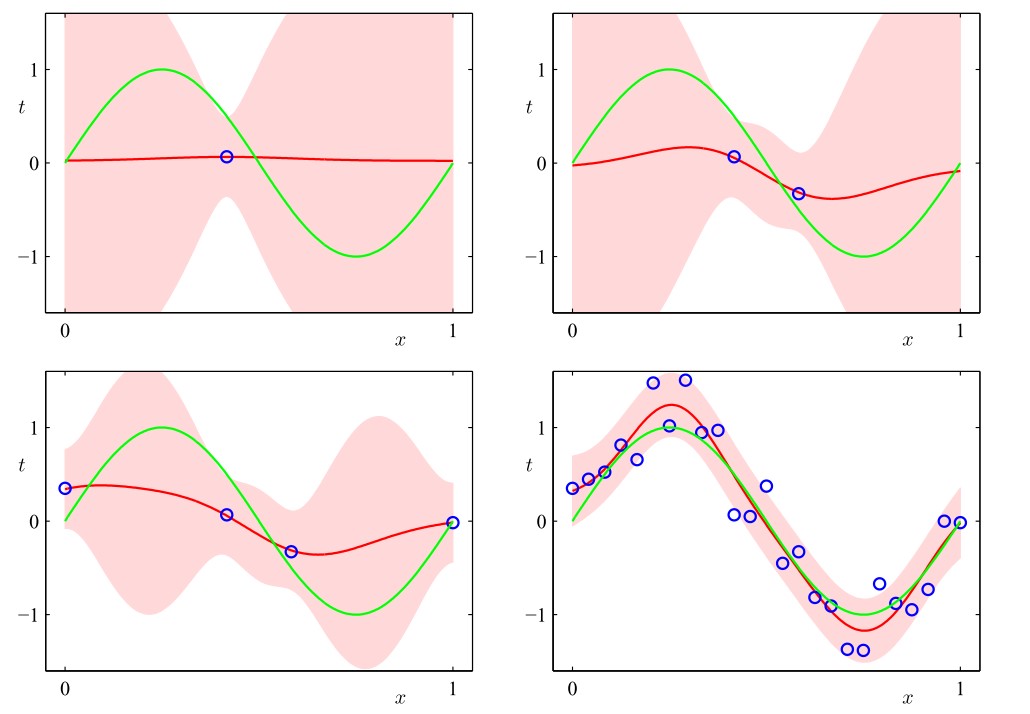
蓝色圆圈表示数据点，红线表示对应的高斯预测分布的均值，红色阴影区域是均值两侧的一个标准差范围的区域。注意，预测的不确定性依赖于xxx，并且在数据点的邻域内最小。还要注意，不确定性的程度随着观测到的数据点的增多而逐渐减小。上图只给出了每个点处的预测方差与xxx的函数关系。为了更加深刻地认识对于不同的xxx值的预测之间的协方差，我们可以从ww\mathbf w的后验概率分布中抽取若干样本，然后画出对应的函数y(x,w)y(x,w)y(x,\mathbf w)，如下图

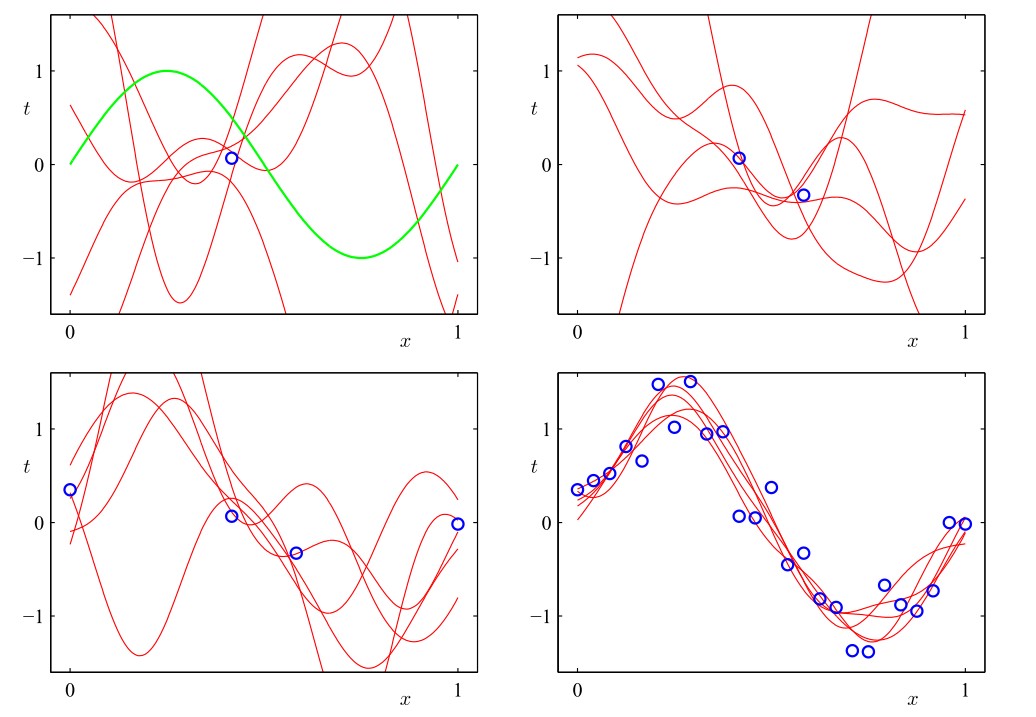
​ ​ ​ 如果我们使用局部的基函数（例如高斯基函数），那么在距离基函数中心比较远的区域，σ2N(x)σN2(x)\sigma_N^2(\mathbf x)表达式中的第二项将会趋于零，只剩下第一项（噪声）β−1β−1\beta^{-1}。因此，当对基函数所在的区域之外的区域进行外插的时候，模型对于它做出的预测会变得相当确定（因为与训练数据集无关，仅与ββ\beta相关的高斯分布有关），这种结果通常是不准确的，使用被称为高斯过程（Gaussian process）的另一种贝叶斯回归方法可以避免这个问题。

​ ​ ​ 最后，如果p(w,β)' role="presentation" style="position: relative;">p(w,β)p(w,β)p(\mathbf w,\beta)是一个高斯-Gamma分布，此时的预测分布是一个t分布。

3.3 等价核

​ ​ ​ 如果我们将mN=βSNΦTtmN=βSNΦTt\mathbf m_N=\beta\mathbf S_N\mathbf\Phi^T\mathbf t视为参数ww\mathbf w的估计值并将其代入y(x,w)=wTϕϕ(x)y(x,w)=wTϕϕ(x)y(\mathbf x,\mathbf w)=\mathbf w^T\pmb\phi(\mathbf x)，那么得到

y(x,w)=y(x,mN)=(βSNΦTt)Tϕϕ(x)y(x,w)=y(x,mN)=(βSNΦTt)Tϕϕ(x)y(\mathbf x,\mathbf w)=y(\mathbf x,\mathbf m_N)=(\beta\mathbf S_N\mathbf\Phi^T\mathbf t)^T\pmb\phi(\mathbf x)
使用PRML 概率分布中3.2小节介绍的Dirac符号，我们可以发现，βSNΦTtβSNΦTt\beta\mathbf S_N\mathbf\Phi^T\mathbf t的形式为|⋯⟩|⋯⟩|\cdots\rangle，因此(βSNΦTt)T(βSNΦTt)T(\beta\mathbf S_N\mathbf\Phi^T\mathbf t)^T的形式为⟨⋯|⟨⋯|\langle\cdots|，又因为ϕϕ(x)ϕϕ(x)\pmb\phi(\mathbf x)的形式为|⋯⟩|⋯⟩|\cdots\rangle，那么(βSNΦTt)Tϕϕ(x)(βSNΦTt)Tϕϕ(x)(\beta\mathbf S_N\mathbf\Phi^T\mathbf t)^T\pmb\phi(\mathbf x)的形式即为⟨⋯⟩⟨⋯⟩\langle\cdots\rangle，即一个数值（而非向量）（因为我们只估计一个目标变量ttt，这一点亦是显而易见的），那么上式可以写成

y(x,mN)=ϕϕ(x)T(βSNΦTt)=∑n=1Nβϕϕ(x)TSNϕϕ(xn)tn=∑n=1Nk(x,xn)tny(x,mN)=ϕϕ(x)T(βSNΦTt)=∑n=1Nβϕϕ(x)TSNϕϕ(xn)tn=∑n=1Nk(x,xn)tny(\mathbf x,\mathbf m_N)=\pmb\phi(\mathbf x)^T(\beta\mathbf S_N\mathbf\Phi^T\mathbf t)=\sum_{n=1}^N\beta\pmb\phi(\mathbf x)^T\mathbf S_N\pmb\phi(\mathbf x_n)t_n=\sum_{n=1}^Nk(\mathbf x,\mathbf x_n)t_n
其中S−1N=αI+βΦTΦSN−1=αI+βΦTΦ\mathbf S_N^{-1}=\alpha\mathbf I+\beta\mathbf\Phi^T\mathbf\Phi，函数k(x,x′)=βϕϕ(x)TSNϕϕ(x′)k(x,x′)=βϕϕ(x)TSNϕϕ(x′)k(\mathbf x,\mathbf x')=\beta\pmb\phi(\mathbf x)^T\mathbf S_N\pmb\phi(\mathbf x')称为平滑矩阵（smoother matrix）或者等价核（equivalent kernel）。像这样的回归函数，通过对目标值进行线性组合做预测，被称为线性平滑（linear smoother）。注意，等价核依赖于训练集（因为SNSN\mathbf S_N的表达式中含有ΦΦ\mathbf\Phi，而ΦΦ\mathbf\Phi的表达式中含有训练集的XX\mathbf X）。

​ ​ ​ 关于等价核，我们可以更加细致地讨论。因为参数xx\mathbf x满足p(w|t)=N(w|mN,SN)p(w|t)=N(w|mN,SN)p(\mathbf w|\mathbf t)=\mathcal N(\mathbf w|\mathbf m_N,\mathbf S_N)，则y(x)y(x)y(\mathbf x)与y(x′)y(x′)y(\mathbf x')的协方差为

cov(y(x),y(x′))=cov(wTϕϕ(x),wTϕϕ(x′))=cov(ϕϕ(x)Tw,wTϕϕ(x′))=E(ϕϕ(x)Tw⋅wTϕϕ(x′))−E(ϕϕ(x)Tw)E(wTϕϕ(x′))=ϕϕ(x)T⋅E(wwT)⋅ϕϕ(x′)−ϕϕ(x)T⋅E(w)⋅E(wT)⋅ϕϕ(x′)=ϕϕ(x)T⋅(E(wwT)−E(w)E(wT))⋅ϕϕ(x′)=ϕϕ(x)T⋅cov(w,wT)⋅ϕϕ(x′)=ϕϕ(x)TSNϕϕ(x′)=β−1k(x,x′)cov(y(x),y(x′))=cov(wTϕϕ(x),wTϕϕ(x′))=cov(ϕϕ(x)Tw,wTϕϕ(x′))=E(ϕϕ(x)Tw⋅wTϕϕ(x′))−E(ϕϕ(x)Tw)E(wTϕϕ(x′))=ϕϕ(x)T⋅E(wwT)⋅ϕϕ(x′)−ϕϕ(x)T⋅E(w)⋅E(wT)⋅ϕϕ(x′)=ϕϕ(x)T⋅(E(wwT)−E(w)E(wT))⋅ϕϕ(x′)=ϕϕ(x)T⋅cov(w,wT)⋅ϕϕ(x′)=ϕϕ(x)TSNϕϕ(x′)=β−1k(x,x′)\begin{aligned}
\text{cov}(y(\mathbf x),y(\mathbf x'))&=\text{cov}(\mathbf w^T\pmb\phi(\mathbf x),\mathbf w^T\pmb\phi(\mathbf x'))\
&=\text{cov}(\pmb\phi(\mathbf x)^T\mathbf w,\mathbf w^T\pmb\phi(\mathbf x'))\
&=
E(\pmb\phi(\mathbf x)^T\mathbf w\cdot\mathbf w^T\pmb\phi(\mathbf x'))-E(\pmb\phi(\mathbf x)^T\mathbf w)E(\mathbf w^T\pmb\phi(\mathbf x'))\
&=\pmb\phi(\mathbf x)^T\cdot E(\mathbf w\mathbf w^T)\cdot\pmb\phi(\mathbf x')-\pmb\phi(\mathbf x)^T\cdot E(\mathbf w)\cdot E(\mathbf w^T)\cdot\pmb\phi(\mathbf x')\
&=\pmb\phi(\mathbf x)^T\cdot(E(\mathbf w\mathbf w^T)-E(\mathbf w)E(\mathbf w^T))\cdot\pmb\phi(\mathbf x')\
&=\pmb\phi(\mathbf x)^T\cdot\text{cov}{(\mathbf w,\mathbf w^T)}\cdot\pmb\phi(\mathbf x')\
&=\pmb\phi(\mathbf x)^T\mathbf S_N\pmb\phi(\mathbf x')\
&=\beta^{-1}k(\mathbf x,\mathbf x')
\end{aligned}
由此我们知道，在已知数据点x′x′\mathbf x'附近进行预测，得到的y(x)y(x)y(\mathbf x)和已知的y(x′)y(x′)y(\mathbf x')相关性较高，而对于较远的xx\mathbf x而言，相关性就较低，上面的几幅图让我们可以直观地感受到这一点。

​ ​ ​ 上面的式子y(x,mN)=∑Nn=1k(x,xn)tny(x,mN)=∑n=1Nk(x,xn)tny(\mathbf x,\mathbf m_N)=\sum_{n=1}^Nk(\mathbf x,\mathbf x_n)t_n暗示了解决回归问题的另一种方法：不显式地引入一组基函数（它隐式地定义了一个等价的核），而是显式地定义一个局部的核函数（它隐式地定义了基函数），然后在给定训练数据集的条件下，用这个核函数对新的输入变量xxx做预测。这就引出了用于回归问题（以及分类问题）的很实用的框架，被称为高斯过程（Gaussian process）。这将在后续内容中讨论。

​ ​ ​ 我们已经看到，一个等价核定义了模型的权值。通过这个权值，训练数据集中的目标值被重新（线性）组合，作为新输入的xx\mathbf x的预测值。可以证明这些权值的和等于111，即∑Nn=1k(x,xn)=1∑n=1Nk(x,xn)=1\sum_{n=1}^Nk(\mathbf x,\mathbf x_n)=1对所有的xx\mathbf x均成立。

​ ​ ​ 对于等价核k(x,x′)=βϕϕ(x)TSNϕϕ(x′)k(x,x′)=βϕϕ(x)TSNϕϕ(x′)k(\mathbf x,\mathbf x')=\beta\pmb\phi(\mathbf x)^T\mathbf S_N\pmb\phi(\mathbf x')而言，它是核函数的一个具体例子。核函数可以为正也可以为负，但必须满足加和为111的限制，除此之外，任意核函数均可以表示为非线性函数的向量ψψ(x)ψψ(x)\pmb\psi(\mathbf x)的内积的形式，即

k(x,z)=ψψ(x)Tψψ(z)k(x,z)=ψψ(x)Tψψ(z)k(\mathbf x,\mathbf z)=\pmb\psi(\mathbf x)^T\pmb\psi(\mathbf z)
对于我们的例子而言，其中ψψ(x)=β1/2S1/2Nϕϕ(x)ψψ(x)=β1/2SN1/2ϕϕ(x)\pmb\psi(\mathbf x)=\beta^{1/2}\mathbf S_N^{1/2}\pmb\phi(\mathbf x)。

4 贝叶斯模型比较

4.1 后验概率与预测分布

​ ​ ​ 在贝叶斯方法中，我们比较不同模型之间的唯一思路就是概率，现假设我们想要比较LLL个模型{Mi}{Mi}{\mathcal M_i}，其中i=1,⋯,Li=1,⋯,Li=1,\cdots,L，“一个模型”指的是训练数据集DDD上的概率分布。在Polynomial Curve Fitting问题中，我们用数据集XX\mathbf X和与之相关的tt\mathbf t表示出了一个模型，这时“概率分布”指的是关于新的目标变量tt\mathbf t的一个概率分布，而输入变量xx\mathbf x是已知的。在一般化的问题中，“概率分布”指的是关于输入变量xx\mathbf x和目标变量tt\mathbf t的一个联合分布p(x,t)p(x,t)p(\mathbf x,\mathbf t)，我们通过积分（连续变量情况下）或者求和（离散变量情况下）得到边缘分布p(x)p(x)p(\mathbf x)和p(t)p(t)p(\mathbf t)。对于LLL个模型中某个模型MiMi\mathcal M_i而言，其后验概率为

p(Mi|D)∝p(Mi)p(D|Mi)p(Mi|D)∝p(Mi)p(D|Mi)p(\mathcal M_i|D)\varpropto p(\mathcal M_i)p(D|\mathcal M_i)
如果后验概率较大，则说明数据集DDD比较支持这个模型MiMi\mathcal M_i，如果后验概率较小则说明其不支持该模型。如果所有的模型都有相同的先验概率p(Mi)p(Mi)p(\mathcal M_i)，那么项p(D|Mi)p(D|Mi)p(D|\mathcal M_i)就表达了数据展现出的不同模型的优先级，该项称为模型证据（model evidence）或者边缘似然（marginal likelihood）（被称为边缘似然因为该项可以视为联合分布p(Mi,D)p(Mi,D)p(\mathcal M_i,D)进行积分或求和得到）。两个模型的模型证据的比值p(D|Mi)p(D|Mj)p(D|Mi)p(D|Mj)\frac{p(D|\mathcal M_i)}{p(D|\mathcal M_j)}称为贝叶斯因子（Bayes factor）。

​ ​ ​ 如果我们知道了所有的模型的后验概率p(Mi|D)p(Mi|D)p(\mathcal M_i|D)，那么就掌握了在（训练）数据集DDD下，LLL个模型的可能性，故此时预测分布为

p(t|x,D)=∑i=1Lp(t|x,Mi,D)p(Mi|D)p(t|x,D)=∑i=1Lp(t|x,Mi,D)p(Mi|D)p(t|\mathbf x,D)=\sum_{i=1}^Lp(t|\mathbf x,\mathcal M_i,D)p(\mathcal M_i|D)
这实际上就是对各个模型的预测分布p(t|x,Mi,D)p(t|x,Mi,D)p(t|\mathbf x,\mathcal M_i,D)进行加权平均，可视作混合分布（mixture distribution）的一个例子。如果有两个模型的后验概率分布p(Mi|D)=p(Mj|D)p(Mi|D)=p(Mj|D)p(\mathcal M_i|D)=p(\mathcal M_j|D)，且一个模型预测为t=at=at=a附近的一个很窄的分布、一个模型预测为t=bt=bt=b附近的一个很窄的分布，那么总体将会是一个双峰分布（而不是t=a+b2t=a+b2t=\frac{a+b}{2}附近的单峰分布）。在具体应用中，一个粗略的思路就是从LLL个模型中选出后验概率最大的模型进行预测。

4.2 模型证据

​ ​ ​ 现在来展开说说模型证据这个概念。对于由参数ww\mathbf w控制的模型而言，其模型证据（边缘似然）为

p(D|Mi)=∫p(D,w|Mi)dw=∫p(D|w,Mi)p(w|Mi)dwp(D|Mi)=∫p(D,w|Mi)dw=∫p(D|w,Mi)p(w|Mi)dwp(D|\mathcal M_i)=\int p(D,\mathbf w|\mathcal M_i)d\mathbf w=\int p(D|\mathbf w,\mathcal M_i)p(\mathbf w|\mathcal M_i)d\mathbf w
从取样的角度来说，这个边缘似然p(D|Mi)p(D|Mi)p(D|\mathcal M_i)可以视作从模型MiMi\mathcal M_i中生成数据集DDD的概率，而模型MiMi\mathcal M_i的参数ww\mathbf w是从先验分布p(w)p(w)p(\mathbf w)（在预先训练一定次数的时候，先验分布就是之前的后验分布p(w|D)p(w|D)p(\mathbf w|D)）中随机取样的。

​ ​ ​ 先来看一个简化的情况：模型只有一个参数www，那么p(w|D)∝p(D|w)p(w)p(w|D)∝p(D|w)p(w)p(w|D)\varpropto p(D|w)p(w)（其中省去了MiMi\mathcal M_i）。如果后验分布在极大似然估计wMAPwMAPw_{MAP}附近有一个尖峰，宽度为Δw后验Δw后验\Delta w_{\text{后验}}，并进一步假设先验分布是平的，且宽度为Δw先验Δw先验\Delta w_{\text{先验}}（即p(w)=1Δw先验p(w)=1Δw先验p(w)=\frac{1}{\Delta w_{\text{先验}}}），那么

p(D|Mi)=∫p(D,w|Mi)dw=∫p(D|w,Mi)p(w|Mi)dw∼p(D|wMAP,Mi)Δw后验Δw先验p(D|Mi)=∫p(D,w|Mi)dw=∫p(D|w,Mi)p(w|Mi)dw∼p(D|wMAP,Mi)Δw后验Δw先验p(D|\mathcal M_i)=\int p(D,w|\mathcal M_i)dw=\int p(D|w,\mathcal M_i)p(w|\mathcal M_i)dw\sim p(D|w_{MAP},\mathcal M_i)\frac{\Delta w_{\text{后验}}}{\Delta w_{\text{先验}}}
取对数可得

lnp(D|Mi)∼lnp(D|wMAP,Mi)+ln(Δw后验Δw先验)ln⁡p(D|Mi)∼ln⁡p(D|wMAP,Mi)+ln⁡(Δw后验Δw先验)\ln p(D|\mathcal M_i)\sim\ln p(D|w_{MAP},\mathcal M_i)+\ln(\frac{\Delta w_{\text{后验}}}{\Delta w_{\text{先验}}})
其中第一项表示由最可能的参数wMAPwMAPw_{MAP}给出的数据，第二项用于根据模型的复杂度来惩罚模型。由于Δw后验<Δw先验Δw后验<Δw先验\Delta w_{\text{后验}}<\Delta w_{\text{先验}}（随着学习过程的进行，不确定度会减小，即会越来越趋于某个尖峰），因此，如果参数精确地调整为后验分布的数据，那么ln(Δw后验Δw先验)<0ln⁡(Δw后验Δw先验)<0\ln(\frac{\Delta w_{\text{后验}}}{\Delta w_{\text{先验}}})<0将会非常小，这非常不利于后验概率p(D|Mi)p(D|Mi)p(D|\mathcal M_i)最大化。

​ ​ ​ 现在来看一般的情况，如果一个模型具有MMM个参数，我们可以对每个参数进行类似的近似，假设所有参数的Δw后验Δw先验Δw后验Δw先验\frac{\Delta w_{\text{后验}}}{\Delta w_{\text{先验}}}均相同，那么

lnp(D|Mi)∼lnp(D|wMAP,Mi)+Mln(Δw后验Δw先验)ln⁡p(D|Mi)∼ln⁡p(D|wMAP,Mi)+Mln⁡(Δw后验Δw先验)\ln p(D|\mathcal M_i)\sim\ln p(D|\mathbf w_{MAP},\mathcal M_i)+M\ln(\frac{\Delta w_{\text{后验}}}{\Delta w_{\text{先验}}})
因此，在这种非常简单的近似下，复杂度惩罚项（上式第二项）的大小（负数）随着可调节参数数量MMM的增加而越来越小。另外，随着MMM的增加，模型能够更加精确地描述数据集，也就是第一项会变大。这就带来了一个矛盾：更多的参数能够更好地描述数据集，但是复杂度上升也会招致惩罚，我们需要在这两方面进行折中。

​ ​ ​ 一般而言，对两个模型∫p(D|Mi)ln⁡(p(D|Mi)p(D|Mj))dD' role="presentation" style="text-align: center; position: relative;">∫p(D|Mi)ln(p(D|Mi)p(D|Mj))dD∫p(D|Mi)ln⁡(p(D|Mi)p(D|Mj))dD\int p(D|\mathcal M_i)\ln(\frac{p(D|\mathcal M_i)}{p(D|\mathcal M_j)})dD
如果模型MjMj\mathcal M_j和模型MiMi\mathcal M_i完全一致，那么上面的KL散度为零，否则恒为正。

​ ​ ​ 我们已经看到，贝叶斯框架避免了过拟合的问题，并且使得模型能够随着训练次数的增加而得到优化。但是贝叶斯方法需要对模型的形式作出假设，并且如果这些假设不合理，那么结果就会出错。特别地，我们从上图可以看出，模型证据对先验分布的很多方面都很敏感，例如在低概率处的行为等等。如果先验分布是反常的，那么模型证据无法定义，因为反常的先验分布有着任意的缩放因子（换句话说，归一化系数无法定义，因为分布根本无法被归一化）。如果我们考虑一个正常的先验分布，然后取一个适当的极限来获得一个反常的先验（例如高斯先验中，我们令方差为无穷大），那么模型证据就会趋于零。但是这种情况下也可能通过首先考虑两个模型的证据比值，然后取极限的方式来得到⼀个有意义的答案。 因此，在实际应用中，一种明智的做法是，保留一个独立的测试数据集，这个数据集用来评估最终系统的整体表现。

5 证据近似

5.1 基本框架介绍

​ ​ ​ 在经典的贝叶斯方法中，我们预先确定了模型的超参数（现在我们假设有两个参数αα\alpha和ββ\beta），然后计算后验概率p(w|D,α,β)p(w|D,α,β)p(\mathbf w|D,\alpha,\beta)，再确定出预测分布p(t|w,x)p(t|w,x)p(t|\mathbf w,\mathbf x)。如果我们引入的是超参数的先验分布（而不是具体的值），那么预测分布需要通过积分方法来求解，即

p(t|t)=∭p(t|w,β)p(w|t,α,β)p(α,β|t)dwdαdβp(t|t)=∭p(t|w,β)p(w|t,α,β)p(α,β|t)dwdαdβp(t|\mathbf t)=\iiint p(t|\mathbf w,\beta)p(\mathbf w|\mathbf t,\alpha,\beta)p(\alpha,\beta|\mathbf t)d\mathbf wd\alpha d\beta
为了记号简洁，上述式子省略了预测分布对xx\mathbf x的依赖。其中p(w|t,α,β)p(w|t,α,β)p(\mathbf w|\mathbf t,\alpha,\beta)为此时参数的后验分布，p(t|w,β)p(t|w,β)p(t|\mathbf w,\beta)为确定参数ww\mathbf w时的预测分布N(t|y(x,w),β−1)N(t|y(x,w),β−1)\mathcal N(t|y(\mathbf x,\mathbf w),\beta^{-1})，p(α,β|t)p(α,β|t)p(\alpha,\beta|\mathbf t)为在训练数据集tt\mathbf t条件下模型超参数αα\alpha和ββ\beta的后验（联合）分布（且该分布p(α,β|t)∝p(t|α,β)p(α,β)p(α,β|t)∝p(t|α,β)p(α,β)p(\alpha,\beta|\mathbf t)\varpropto p(\mathbf t|\alpha,\beta)p(\alpha,\beta)），所以，如果我们先对参数ww\mathbf w进行积分得到边缘似然函数（marginal likelihood function），那么预测分布就是超参数的积分，从统计意义上来说，关于超参数的积分即为超参数条件下预测目标变量ttt的条件分布），故只需要考虑将这个边缘似然函数最大化，便能得到超参数的值，这个框架在统计学文献中称为经验贝叶斯（empirical Bayes）或者第二类极大似然（type 2 maximum likelihood）或者推广的最大似然（generalized maximum likelihood），在机器学习文献中，这种方法也被称为证据近似（evidence approximation）。考虑到p(α,β|t)∝p(t|α,β)p(α,β)p(α,β|t)∝p(t|α,β)p(α,β)p(\alpha,\beta|\mathbf t)\varpropto p(\mathbf t|\alpha,\beta)p(\alpha,\beta)，如果先验分布p(α,β)p(α,β)p(\alpha,\beta)比较平，那么边缘似然函数最大化就等价于将证据函数p(t|α,β)p(t|α,β)p(\mathbf t|\alpha,\beta)最大化，这样得到的参数αα\alpha和ββ\beta的极大似然估计不妨记为α^α^\hat{\alpha}和β^β^\hat{\beta}。一个简单的近似情况是：如果后验分布p(α,β|t)p(α,β|t)p(\alpha,\beta|\mathbf t)在α^α^\hat{\alpha}和β^β^\hat{\beta}附近有峰值，那么上述积分可以近似为

p(t|t)∼p(t|t,α^,β^)=∫p(t|w,β^)p(w|t,α^,β^)dwp(t|t)∼p(t|t,α^,β^)=∫p(t|w,β^)p(w|t,α^,β^)dwp(t|\mathbf t)\sim p(t|\mathbf t,\hat{\alpha},\hat{\beta})=\int p(t|\mathbf w,\hat{\beta})p(\mathbf w|\mathbf t,\hat{\alpha},\hat{\beta})d\mathbf w
​ ​ ​ 在上面介绍的方法中，模型超参数αα\alpha和ββ\beta是通过训练数据集得到的，这种方法具有很好的实用性。对于证据函数p(t|α,β)p(t|α,β)p(\mathbf t|\alpha,\beta)最大化而言，有两种常见的方法：一是计算证据函数并令证据函数的导数等于零，这将在接下来进行讨论；二是期望最大化（EM）方法，这将在后续章节进行讨论。

5.2 计算证据函数

​ ​ ​ 求证据函数的第一步是对权值参数ww\mathbf w进行积分，即

p(t|α,β)=∫p(t|w,α,β)p(w|α)dw=∫N(t|wTϕϕ(xn),β−1)⋅N(w|0,α−1I)dw=∫∏n=1NN(tn|wTϕϕ(xn),β−1)⋅∏m=1MN(wm|0,α−1I)dw=(β2π)N/2(α2π)M/2∫N(tn|wTϕϕ(xn),β−1)⋅N(wm|0,α−1I)dw=(β2π)N/2(α2π)M/2∬⋯∫N(tn|wTϕϕ(xn),β−1)⋅N(wm|0,α−1I)dw1dw2⋯dwM=⋯p(t|α,β)=∫p(t|w,α,β)p(w|α)dw=∫N(t|wTϕϕ(xn),β−1)⋅N(w|0,α−1I)dw=∫∏n=1NN(tn|wTϕϕ(xn),β−1)⋅∏m=1MN(wm|0,α−1I)dw=(β2π)N/2(α2π)M/2∫N(tn|wTϕϕ(xn),β−1)⋅N(wm|0,α−1I)dw=(β2π)N/2(α2π)M/2∬⋯∫N(tn|wTϕϕ(xn),β−1)⋅N(wm|0,α−1I)dw1dw2⋯dwM=⋯\begin{aligned}
p(\mathbf t|\alpha,\beta)&=\int p(\mathbf t|\mathbf w,\alpha,\beta)p(\mathbf w|\alpha)d\mathbf w\
&=\int\mathcal N(\mathbf t|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1})\cdot\mathcal N(\mathbf w|\mathbf 0,\alpha^{-1}\mathbf I)d\mathbf w\
&=\int\prod_{n=1}^N\mathcal N(t_n|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1})\cdot\prod_{m=1}^M\mathcal N(w_m|\mathbf 0,\alpha^{-1}\mathbf I)d\mathbf w\
&=(\frac{\beta}{2\pi})^{N/2}(\frac{\alpha}{2\pi})^{M/2}\int\mathcal N(t_n|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1})\cdot\mathcal N(w_m|\mathbf 0,\alpha^{-1}\mathbf I)d\mathbf w\
&=(\frac{\beta}{2\pi})^{N/2}(\frac{\alpha}{2\pi})^{M/2}\iint\cdots\int\mathcal N(t_n|\mathbf w^T\pmb\phi(\mathbf x_n),\beta^{-1})\cdot\mathcal N(w_m|\mathbf 0,\alpha^{-1}\mathbf I)dw_1dw_2\cdots dw_M\
&=\cdots
\end{aligned}
除了上面逐步推导的思路，我们还可以用PRML 概率分布中3.7小节介绍的结论，得到

p(t|α,β)=(β2π)N/2(α2π)M/2∫exp(−E(w))dwE(w)=βED(w)+αEW(w)=β2||t−Φw||2+α2wTwp(t|α,β)=(β2π)N/2(α2π)M/2∫exp(−E(w))dwE(w)=βED(w)+αEW(w)=β2||t−Φw||2+α2wTwp(\mathbf t|\alpha,\beta)=(\frac{\beta}{2\pi})^{N/2}(\frac{\alpha}{2\pi})^{M/2}\int\text{exp}(-E(\mathbf w))d\mathbf w\
E(\mathbf w)=\beta E_D(\mathbf w)+\alpha E_W(\mathbf w)=\frac\beta2||\mathbf t-\mathbf\Phi\mathbf w||^2+\frac\alpha2\mathbf w^T\mathbf w
其中E(w)E(w)E(\mathbf w)在形式上和正则化的误差函数12∑Nn=1{tn−wTϕϕ(xn)}2+λ2wTw12∑n=1N{tn−wTϕϕ(xn)}2+λ2wTw\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2+\frac\lambda2\mathbf w^T\mathbf w相似。我们现在对参数ww\mathbf w配方，过程如下

E(w)=β2||t−Φw||2+α2wTw=β2(t−Φw)T(t−Φw)+α2wTw=β2(tTt−tTΦw−(Φw)Tt+(Φw)T(Φw))+α2wTw=β2(tTt−tTΦw−(Φw)Tt)+12(wT(βΦTΦ)w+wT(αI)w)=β2(tTt−tTΦw−(Φw)Tt)+12wTAw,A=βΦTΦ+αI=S−1N=12(βtTt−βtTΦw−β(Φw)Tt+wTAw)=12(βtTt−2βtTΦw+wTAw)=12((w−mN)TA(w−mN)−mTNAmN+βtTt),mN=βSNΦTt+12(β(t−ΦmN)T(t−ΦmN)−β(t−ΦmN)T(t−ΦmN))=12((w−mN)TA(w−mN)−mTNAmN+βtTt)+12(β(t−ΦmN)T(t−ΦmN)−βtTt+2βtTΦmN−βmTN(ΦTΦ)mN)=12(−mTNAmN+βtTt−βtTt+2βtTΦmN−βmTN(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mTNAmN+2βtTΦmN−βmTN(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mTNAmN+2β(β−1mTNAT)mN−βmTN(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mTNAmN+2β(β−1mTNA)mN−βmTN(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mTNAmN+2mTNAmN−βmTN(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(mTNAmN−mTN(βΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12mTN(αI)mN+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=α2mTNmN+12(w−mN)TA(w−mN)+β2||t−ΦmN||2=E(mN)+12(w−mN)TA(w−mN)E(w)=β2||t−Φw||2+α2wTw=β2(t−Φw)T(t−Φw)+α2wTw=β2(tTt−tTΦw−(Φw)Tt+(Φw)T(Φw))+α2wTw=β2(tTt−tTΦw−(Φw)Tt)+12(wT(βΦTΦ)w+wT(αI)w)=β2(tTt−tTΦw−(Φw)Tt)+12wTAw,A=βΦTΦ+αI=SN−1=12(βtTt−βtTΦw−β(Φw)Tt+wTAw)=12(βtTt−2βtTΦw+wTAw)=12((w−mN)TA(w−mN)−mNTAmN+βtTt),mN=βSNΦTt+12(β(t−ΦmN)T(t−ΦmN)−β(t−ΦmN)T(t−ΦmN))=12((w−mN)TA(w−mN)−mNTAmN+βtTt)+12(β(t−ΦmN)T(t−ΦmN)−βtTt+2βtTΦmN−βmNT(ΦTΦ)mN)=12(−mNTAmN+βtTt−βtTt+2βtTΦmN−βmNT(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mNTAmN+2βtTΦmN−βmNT(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mNTAmN+2β(β−1mNTAT)mN−βmNT(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mNTAmN+2β(β−1mNTA)mN−βmNT(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(−mNTAmN+2mNTAmN−βmNT(ΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12(mNTAmN−mNT(βΦTΦ)mN)+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=12mNT(αI)mN+12(w−mN)TA(w−mN)+12β(t−ΦmN)T(t−ΦmN)=α2mNTmN+12(w−mN)TA(w−mN)+β2||t−ΦmN||2=E(mN)+12(w−mN)TA(w−mN)\begin{aligned}
E(\mathbf w)&=\frac\beta2||\mathbf t-\mathbf\Phi\mathbf w||^2+\frac\alpha2\mathbf w^T\mathbf w\
&=\frac\beta2(\mathbf t-\mathbf\Phi\mathbf w)^T(\mathbf t-\mathbf\Phi\mathbf w)+\frac\alpha2\mathbf w^T\mathbf w\
&=\frac\beta2(\mathbf t^T\mathbf t-\mathbf t^T\mathbf\Phi\mathbf w-(\mathbf\Phi\mathbf w)^T\mathbf t+(\mathbf\Phi\mathbf w)^T(\mathbf\Phi\mathbf w))+\frac\alpha2\mathbf w^T\mathbf w\
&=\frac\beta2(\mathbf t^T\mathbf t-\mathbf t^T\mathbf\Phi\mathbf w-(\mathbf\Phi\mathbf w)^T\mathbf t)+\frac12(\mathbf w^T(\beta\mathbf\Phi^T\mathbf\Phi)\mathbf w+\mathbf w^T(\alpha\mathbf I)\mathbf w)\
&=\frac\beta2(\mathbf t^T\mathbf t-\mathbf t^T\mathbf\Phi\mathbf w-(\mathbf\Phi\mathbf w)^T\mathbf t)+\frac12\mathbf w^T\mathbf A\mathbf w,\quad\mathbf A=\beta\mathbf\Phi^T\mathbf\Phi+\alpha\mathbf I=\mathbf S_N^{-1}\
&=\frac12(\beta\mathbf t^T\mathbf t-\beta\mathbf t^T\mathbf\Phi\mathbf w-\beta(\mathbf\Phi\mathbf w)^T\mathbf t+\mathbf w^T\mathbf A\mathbf w)\
&=\frac12(\beta\mathbf t^T\mathbf t-2\beta\mathbf t^T\mathbf\Phi\mathbf w+\mathbf w^T\mathbf A\mathbf w)\
&=\frac12((\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)-\mathbf m_N^T\mathbf A\mathbf m_N+\beta\mathbf t^T\mathbf t),\quad\mathbf m_N=\beta\mathbf S_N\mathbf\Phi^T\mathbf t\
&\qquad+\frac12(\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)-\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N))\
&=\frac12((\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)-\mathbf m_N^T\mathbf A\mathbf m_N+\beta\mathbf t^T\mathbf t)\
&\qquad+\frac12(\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)-\beta\mathbf t^T\mathbf t+2\beta\mathbf t^T\mathbf\Phi\mathbf m_N-\beta\mathbf m_N^T(\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&=\frac12(-\mathbf m_N^T\mathbf A\mathbf m_N+\beta\mathbf t^T\mathbf t-\beta\mathbf t^T\mathbf t+2\beta\mathbf t^T\mathbf\Phi\mathbf m_N-\beta\mathbf m_N^T(\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&\qquad+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac12(-\mathbf m_N^T\mathbf A\mathbf m_N+2\beta\mathbf t^T\mathbf\Phi\mathbf m_N-\beta\mathbf m_N^T(\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&\qquad+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac12(-\mathbf m_N^T\mathbf A\mathbf m_N+2\beta(\beta^{-1}\mathbf m_N^T\mathbf A^T)\mathbf m_N-\beta\mathbf m_N^T(\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&\qquad+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac12(-\mathbf m_N^T\mathbf A\mathbf m_N+2\beta(\beta^{-1}\mathbf m_N^T\mathbf A)\mathbf m_N-\beta\mathbf m_N^T(\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&\qquad+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac12(-\mathbf m_N^T\mathbf A\mathbf m_N+2\mathbf m_N^T\mathbf A\mathbf m_N-\beta\mathbf m_N^T(\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&\qquad+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac12(\mathbf m_N^T\mathbf A\mathbf m_N-\mathbf m_N^T(\beta\mathbf\Phi^T\mathbf\Phi)\mathbf m_N)\
&\qquad+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac12\mathbf m_N^T(\alpha\mathbf I)\mathbf m_N+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac12\beta(\mathbf t-\mathbf\Phi\mathbf m_N)^T(\mathbf t-\mathbf\Phi\mathbf m_N)\
&=\frac\alpha2\mathbf m_N^T\mathbf m_N+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)+\frac\beta2||\mathbf t-\mathbf\Phi\mathbf m_N||^2\
&=E(\mathbf m_N)+\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)
\end{aligned}
其中E(mN)=β2||t−ΦmN||2+α2mTNmNE(mN)=β2||t−ΦmN||2+α2mNTmNE(\mathbf m_N)=\frac\beta2||\mathbf t-\mathbf\Phi\mathbf m_N||^2+\frac\alpha2\mathbf m_N^T\mathbf m_N，此时矩阵AA\mathbf A就是误差函数E(w)E(w)E(\mathbf w)的二阶导数∇∇E(w)∇∇E(w)\nabla\nabla E(\mathbf w)，称为Hessian矩阵。上述推导过程还得到一个副产品A=S−1NA=SN−1\mathbf A=\mathbf S_N^{-1}，这给出了方差的数学依据。

​ ​ ​ 现在，关于ww\mathbf w的积分∫exp(−E(w))dw∫exp(−E(w))dw\int\text{exp}(-E(\mathbf w))d\mathbf w可以计算为

∫exp(−E(w))dw=exp(E(mN))∫exp{12(w−mN)TA(w−mN)}dw=exp(E(mN))⋅(2π)M/2|A|−1/2∫exp(−E(w))dw=exp(E(mN))∫exp{12(w−mN)TA(w−mN)}dw=exp(E(mN))⋅(2π)M/2|A|−1/2\begin{aligned}
\int\text{exp}(-E(\mathbf w))d\mathbf w&=\text{exp}(E(\mathbf m_N))\int\text{exp}{\frac12(\mathbf w-\mathbf m_N)^T\mathbf A(\mathbf w-\mathbf m_N)}d\mathbf w\
&=\text{exp}(E(\mathbf m_N))\cdot(2\pi)^{M/2}|\mathbf A|^{-1/2}
\end{aligned}
则边缘似然函数p(t|α,β)p(t|α,β)p(\mathbf t|\alpha,\beta)的对数可以写为

lnp(t|α,β)=M2lnα+N2lnβ−E(mN)−12ln|A|−N2ln(2π)ln⁡p(t|α,β)=M2ln⁡α+N2ln⁡β−E(mN)−12ln⁡|A|−N2ln⁡(2π)\ln p(\mathbf t|\alpha,\beta)=\frac{M}{2}\ln\alpha+\frac{N}{2}\ln\beta-E(\mathbf m_N)-\frac12\ln|\mathbf A|-\frac{N}{2}\ln(2\pi)
这就是证据函数的表达式。

​ ​ ​ 现在，如果我们将证据函数关于αα\alpha（ββ\beta）求偏导，那么便可以分析得到αα\alpha（ββ\beta）取何值时，证据函数有极值，也就是说，此时的参数αα\alpha（和参数ββ\beta）是在训练过程中确定的，而12∑Nn=1{tn−wTϕϕ(xn)}2+λ2wTw12∑n=1N{tn−wTϕϕ(xn)}2+λ2wTw\frac12\sum_{n=1}^N{t_n-\mathbf w^T\pmb\phi(\mathbf x_n)}^2+\frac\lambda2\mathbf w^T\mathbf w的惩罚项因子λλ\lambda却是预先确定的，当值选取不合适的时候，模型拟合效果就会很差，在训练过程中不断修正参数值的思路比预先确定参数的值要更好、所得到的模型拟合得也更好。

5.3 最大化证据函数

​ ​ ​ 先考虑边缘似然函数p(t|α,β)p(t|α,β)p(\mathbf t|\alpha,\beta)对参数αα\alpha的最大化，在lnp(t|α,β)ln⁡p(t|α,β)\ln p(\mathbf t|\alpha,\beta)中，M2lnα−E(mN)M2ln⁡α−E(mN)\frac{M}{2}\ln\alpha-E(\mathbf m_N)可以直接地对αα\alpha求偏导，N2lnβ−N2ln(2π)N2ln⁡β−N2ln⁡(2π)\frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)与αα\alpha无关，所以现在只需要考虑如何对ln|A|ln⁡|A|\ln|\mathbf A|求αα\alpha的偏导即可。考虑到A=βΦTΦ+αIA=βΦTΦ+αI\mathbf A=\beta\mathbf\Phi^T\mathbf\Phi+\alpha\mathbf I，矩阵βΦTΦβΦTΦ\beta\mathbf\Phi^T\mathbf\Phi的特征值满足(βΦTΦ)ui=λiui(βΦTΦ)ui=λiui(\beta\mathbf\Phi^T\mathbf\Phi)\mathbf u_i=\lambda_i\mathbf u_i，因此AA\mathbf A的特征值为λi+αλi+α\lambda_i+\alpha，因此|A|=∏i=1(λi+α)|A|=∏i=1(λi+α)|\mathbf A|=\prod_{i=1}(\lambda_i+\alpha)​，故驻点满足

∂∂αlnp(t|α,β)=M2α−∂∂αE(mN)−12∂∂αln|A|=M2α−12mTNmN−12∑i1λi+α=0∂∂αln⁡p(t|α,β)=M2α−∂∂αE(mN)−12∂∂αln⁡|A|=M2α−12mNTmN−12∑i1λi+α=0\begin{aligned}
\frac{\partial}{\partial\alpha}\ln p(\mathbf t|\alpha,\beta)&=\frac{M}{2\alpha}-\frac{\partial}{\partial\alpha}E(\mathbf m_N)-\frac12\frac{\partial}{\partial\alpha}\ln|\mathbf A|\
&=\frac{M}{2\alpha}-\frac12\mathbf m_N^T\mathbf m_N-\frac12\sum_i\frac{1}{\lambda_i+\alpha}=0
\end{aligned}
解得

α=γmTNmN,其中γ=∑iλiλi+αα=γmNTmN,其中γ=∑iλiλi+α\alpha=\frac{\gamma}{\mathbf m_N^T\mathbf m_N},\quad\text{其中}\gamma=\sum_i\frac{\lambda_i}{\lambda_i+\alpha}
这是αα\alpha的一个隐式解，在实际应用中，我们采用迭代的方法求解：首先选定一个初始的αα\alpha的值，使用这个值计算出mN=βSNΦTtmN=βSNΦTt\mathbf m_N=\beta\mathbf S_N\mathbf\Phi^T\mathbf t的值，然后计算出此时的γγ\gamma，从而得到新的αα\alpha的值。注意，由于矩阵ΦTΦΦTΦ\mathbf\Phi^T\mathbf\Phi是固定的，因此可以在最开始计算以此特征值，然后接下来只需要乘以ββ\beta就可以得到λiλi\lambda_i的值。

​ ​ ​ 此时的参数αα\alpha仅通过训练参数集确定的，最极大似然方法不同，最优化模型复杂度不需要单独的数据集。

​ ​ ​ 接下来考虑参数ββ\beta，lnp(t|α,β)ln⁡p(t|α,β)\ln p(\mathbf t|\alpha,\beta)对ββ\beta​求偏导得到

∂∂βlnp(t|α,β)=N2β−∂∂βE(mN)−12∂∂βln|A|=N2β−12∑n=1N{tn−mTNϕϕ(xn)}2−γ2β=0∂∂βln⁡p(t|α,β)=N2β−∂∂βE(mN)−12∂∂βln⁡|A|=N2β−12∑n=1N{tn−mNTϕϕ(xn)}2−γ2β=0\begin{aligned}
\frac{\partial}{\partial\beta}\ln p(\mathbf t|\alpha,\beta)&=\frac{N}{2\beta}-\frac{\partial}{\partial\beta}E(\mathbf m_N)-\frac12\frac{\partial}{\partial\beta}\ln|\mathbf A|\
&=\frac{N}{2\beta}-\frac12\sum_{n=1}^N{t_n-\mathbf m_N^T\pmb\phi(\mathbf x_n)}^2-\frac{\gamma}{2\beta}=0
\end{aligned}
需要注意，虽然mNmN\mathbf m_N的表达式中仍含有参数ββ\beta，但在迭代方法中，这个ββ\beta是预先确定的，因此不需要考虑偏导。解得

1β=1N−γ∑n=1N{tn−mTNϕϕ(xn)}21β=1N−γ∑n=1N{tn−mNTϕϕ(xn)}2\frac1\beta=\frac1{N-\gamma}\sum_{n=1}^N{t_n-\mathbf m_N^T\pmb\phi(\mathbf x_n)}^2
这也是ββ\beta的一个隐式解，使用和αα\alpha类似的迭代方法可以求解。

5.4 参数的有效数量

​ ​ ​ 先分析下面的一幅图从而得到一些有趣的结论

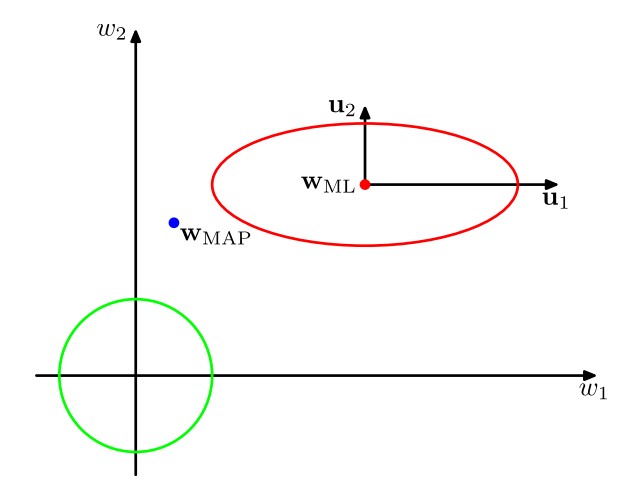
图中绿线表示似然函数ui' role="presentation" style="position: relative;">uiui\mathbf u_i就是椭球各个轴的方向，当时的特征值λiλi\lambda_i指的是协方差ΣΣ\mathbf\Sigma的特征值，此时的λiλi\lambda_i越大则椭球在对应的方向uiui\mathbf u_i上越突出（因为在此方向上的不确定性大）；而这里的特征值λiλi\lambda_i指的是矩阵βΦTΦβΦTΦ\beta\mathbf\Phi^T\mathbf\Phi的特征值，这个矩阵是从S−1N=αI+βΦTΦSN−1=αI+βΦTΦ\mathbf S_N^{-1}=\alpha\mathbf I+\beta\mathbf\Phi^T\mathbf\Phi中得到的、即是从协方差矩阵的逆矩阵得到的，因此此时的λiλi\lambda_i越大则椭球在对应方向uiui\mathbf u_i上越不突出。另外，由于矩阵βΦTΦβΦTΦ\beta\mathbf\Phi^T\mathbf\Phi是正定的，因此比值λiλi+αλiλi+α\frac{\lambda_i}{\lambda_i+\alpha}介于000与111之间，所以γ=∑iλiλi+αγ=∑iλiλi+α\gamma=\sum_i\frac{\lambda_i}{\lambda_i+\alpha}介于000与MMM之间，如果某方向上的λi>>αλi>>α\lambda_i>>\alpha（即比值λiλi+αλiλi+α\frac{\lambda_i}{\lambda_i+\alpha}接近111），那么对应的参数wiwiw_i会与它的极大似然解相近，这样的参数称为良好确定的（well determined），因为它们的值被数据紧紧地限制着。相反，对于λi<<αλi<<α\lambda_i<<\alpha的方向，对应的参数wiwiw_i会与它的先验更加相近（在上图中，即与000更加相近）。特别地，如果所有的特征值λiλi\lambda_i都特别小，那么我们的训练结果wMAPwMAP\mathbf w_{MAP}将会极为接近先验的零均值，在实际意义上，这就相当于我们白训练了、训练基本没什么效果。因此，γ=∑iλiλi+αγ=∑iλiλi+α\gamma=\sum_i\frac{\lambda_i}{\lambda_i+\alpha}度量了良好确定的参数的有效总数。

​ ​ ​ 对于满足高斯分布的单一变量xxx而言，方差的极大似然估计为

σ2ML=1N∑n=1N(xn−μML)2σML2=1N∑n=1N(xn−μML)2\sigma_{ML}^2=\frac1N\sum_{n=1}^N(x_n-\mu_{ML})^2
但是这个估计是有偏的，因为均值的极大似然解μMLμML\mu_{ML}拟合了数据中的一些噪声。方差的无偏估计为

σ2MAP=1N−1∑n=1N(xn−μML)2σMAP2=1N−1∑n=1N(xn−μML)2\sigma_{MAP}^2=\frac1{N-1}\sum_{n=1}^N(x_n-\mu_{ML})^2
而对于线性模型的一般结果，目标分布的均值现在由函数wTϕϕ(x)wTϕϕ(x)\mathbf w^T\pmb\phi(\mathbf x)给出，这包含了MMM个参数，但是由数据良好确定的参数的有效总数仅为γγ\gamma（而非MMM）个，剩余的M−γM−γM-\gamma个参数应该被先验地设为较小的值（因为此时对应的参数wiwiw_i会与它的先验更加相近，即相当于白训练了，故先验会较大程度地影响最后的结果，所以需要尽可能减小先验对最终结果的影响）。对于极限情况N>>MN>>MN>>M（即训练数据集中数据点的数量NNN远大于参数的数量MMM），那么矩阵βΦTΦβΦTΦ\beta\mathbf\Phi^T\mathbf\Phi的模|βΦTΦ||βΦTΦ||\beta\mathbf\Phi^T\mathbf\Phi|将会变得很大（因为模等于特征值之积），所以现在0≤γ≤M0≤γ≤M0\leq\gamma\leq M中的γγ\gamma将会大大倾向于MMM，在极限情况γ=Mγ=M\gamma=M的情况下，参数估计为

α=γmTNmN∼M2EW(mN)β=N−γ∑Nn=1{tn−mTNϕϕ(xn)}2∼N2ED(mN)α=γmNTmN∼M2EW(mN)β=N−γ∑n=1N{tn−mNTϕϕ(xn)}2∼N2ED(mN)\alpha=\frac{\gamma}{\mathbf m_N^T\mathbf m_N}\sim\frac{M}{2E_W(\mathbf m_N)}\
\beta=\frac{N-\gamma}{\sum_{n=1}^N{t_n-\mathbf m_N^T\pmb\phi(\mathbf x_n)}^2}\sim\frac{N}{2E_D(\mathbf m_N)}
其中EWEWE_W和EDEDE_D的定义在前面已经提到过，ββ\beta的分子本来应该近似为N−MN−MN-M，但由于N>>MN>>MN>>M，因此也可以近似为NNN。这些结果可以用作完整的重新估计公式的简化计算的近似，因为它们不需要计算Hessian矩阵的一系列特征值。

6 固定基函数的局限性

​ ​ ​ 在本章中，我们已经关注了由固定的非线性基函数的线性组合组成的模型。我们已经看到，对于参数的线性性质的假设产生了一系列有用的性质，包括最小平方问题的解析解，以及容易计算的贝叶斯方法。此外，对于一个合适的基函数的选择，我们可以建立输入向量到目标值之间的任意非线性映射。在下一章中，我们会研究类似的用于分类的模型。

​ ​ ​ 因此，似乎这样的模型建立的解决模式是识别问题的通用框架。不幸的是，线性模型有一些重要的局限性，这使得我们在后续的章节中要转而关注更加复杂的模型，例如支持向量机和神经网络。

​ ​ ​ 困难的产生主要是因为我们假设了基函数在观测到任何数据之前就被固定了下来，而这正是维数灾难问题的一个表现形式。结果，基函数的数量随着输入空间的维度DDD迅速增长（通常是指数方式增长）。

​ ​ ​ 幸运的是，真实数据集有两个性质，可以帮助我们缓解这个问题。第一，数据向量{xn}{xn}{x_n}通常位于一个非线性流形内部。由于输入变量之间的相关性，这个流形本身的维度小于输入空间的维度。我们将在后面讨论手写数字识别时给出一个例子来说明这一点。如果我们使用局部基函数，那么我们可以让基函数只分布在输入空间中包含数据的区域。这种方法被用在径向基函数网络中，也被用在支持向量机和相关向量机当中。神经网络模型使用可调节的基函数，这些基函数有着sigmoid非线性的性质。神经网络可以通过调节参数，使得在输入空间的区域中基函数会按照数据流形发生变化。第二，目标变量可能只依赖于数据流形中的少量可能的方向。利用这个性质，神经网络可以通过选择输入空间中基函数产生响应的方向。

7 参考资料

• Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006
• Markus Svensen, Christopher M. Bishop, Pattern Recognition and Machine Learning - Solutions to the Exercises: Tutors’ Edition, Springer, 2009
• 马春鹏，《模式识别与机器学习》（本文部分名词翻译来自此书），PRML的网传中文版，2014
• S函数
• 双曲函数
• 偏置-方差分解
• 数据科学导论 Page47
• Delta函数
• PRML 模式识别和机器学习 从零开始的公式推导 3.5 证据近似 3.5.1 计算证据函数
• PRML 模式识别和机器学习 从零开始的公式推导 3.5.3参数的有效数量 3.6固定基函数的局限性
  

转载请注明：xuhss » PRML 回归的线性模型