前言

前期回顾： Python机器学习基础篇一《为什么用Python进行机器学习》

前面说过，监督学习是最常用也是最成功的机器学习类型之一。本章将会详细介绍监督学 习，并解释几种常用的监督学习算法。我们在第 1 章已经见过一个监督学习的应用：利用 物理测量数据将鸢尾花分成几个品种。

记住，每当想要根据给定输入预测某个结果，并且还有输入 / 输出对的示例时，都应该使 用监督学习。这些输入 / 输出对构成了训练集，我们利用它来构建机器学习模型。我们的 目标是对从未见过的新数据做出准确预测。监督学习通常需要人力来构建训练集，但之后 的任务本来非常费力甚至无法完成，现在却可以自动完成，通常速度也更快。

2.1　分类与回归

监督机器学习问题主要有两种，分别叫作分类（classification）与回归（regression）。

分类问题的目标是预测类别标签（class label），这些标签来自预定义的可选列表。第 1 章讲过一个例子，即将鸢尾花分到三个可能的品种之一。分类问题有时可分为二分类 （binary classification，在两个类别之间进行区分的一种特殊情况）和多分类（multiclass classification，在两个以上的类别之间进行区分）。你可以将二分类看作是尝试回答一道是 / 否问题。将电子邮件分为垃圾邮件和非垃圾邮件就是二分类问题的实例。在这个二分类任 务中，要问的是 / 否问题为：“这封电子邮件是垃圾邮件吗？”

在二分类问题中，我们通常将其中一个类别称为正类（positive class），另一个类别称为反 类（negative class）。这里的“正”并不代表好的方面或正数，而是代表研究对象。因此在 寻找垃圾邮件时，“正”可能指的是垃圾邮件这一类别。将两个类别中的哪一个作为“正 类”，往往是主观判断，与具体的领域有关。

另一方面，鸢尾花的例子则属于多分类问题。另一个多分类的例子是根据网站上的文本预测网站所用的语言。这里的类别就是预定义的语言列表。

回归任务的目标是预测一个连续值，编程术语叫作浮点数（floating-point number），数学术 语叫作实数（real number）。根据教育水平、年龄和居住地来预测一个人的年收入，这就是 回归的一个例子。在预测收入时，预测值是一个金额（amount），可以在给定范围内任意 取值。回归任务的另一个例子是，根据上一年的产量、天气和农场员工数等属性来预测玉 米农场的产量。同样，产量也可以取任意数值。

区分分类任务和回归任务有一个简单方法，就是问一个问题：输出是否具有某种连续性。 如果在可能的结果之间具有连续性，那么它就是一个回归问题。想想预测年收入的例子。 输出具有非常明显的连续性。一年赚 40 000 美元还是 40 001 美元并没有实质差别，即使 两者金额不同。如果我们的算法在本应预测 40 000 美元时的预测结果是 39 999 美元或 40 001 美元，不必过分在意。

与此相反，对于识别网站语言的任务（这是一个分类问题）来说，并不存在程度问题。网 站使用的要么是这种语言，要么是那种语言。在语言之间不存在连续性，在英语和法语之 间不存在其他语言。

2.2　泛化、过拟合与欠拟合

在监督学习中，我们想要在训练数据上构建模型，然后能够对没见过的新数据（这些新数据与训练集具有相同的特性）做出准确预测。如果一个模型能够对没见过的数据做出准确 预测，我们就说它能够从训练集泛化（generalize）到测试集。我们想要构建一个泛化精度 尽可能高的模型。

通常来说，我们构建模型，使其在训练集上能够做出准确预测。如果训练集和测试集足够 相似，我们预计模型在测试集上也能做出准确预测。不过在某些情况下这一点并不成立。 例如，如果我们可以构建非常复杂的模型，那么在训练集上的精度可以想多高就多高。

为了说明这一点，我们来看一个虚构的例子。比如有一个新手数据科学家，已知之前船的 买家记录和对买船不感兴趣的顾客记录，想要预测某个顾客是否会买船。目标是向可能购 买的人发送促销电子邮件，而不去打扰那些不感兴趣的顾客。

假设我们有顾客记录，如表 2-1 所示。

表2-1：顾客数据示例

对数据观察一段时间之后，我们的新手数据科学家发现了以下规律：“如果顾客年龄大于 45 岁，并且子女少于 3 个或没有离婚，那么他就想要买船。”如果你问他这个规律的效果 如何，我们的数据科学家会回答：“100% 准确！”的确，对于表中的数据，这条规律完全 正确。我们还可以发现好多规律，都可以完美解释这个数据集中的某人是否想要买船。数 据中的年龄都没有重复，因此我们可以这样说：66、52、53 和 58 岁的人想要买船，而其 他年龄的人都不想买。虽然我们可以编出许多条适用于这个数据集的规律，但要记住，我 们感兴趣的并不是对这个数据集进行预测，我们已经知道这些顾客的答案。我们想知道新 顾客是否可能会买船。因此，我们想要找到一条适用于新顾客的规律，而在训练集上实现 100% 的精度对此并没有帮助。我们可能认为数据科学家发现的规律无法适用于新顾客。 它看起来过于复杂，而且只有很少的数据支持。例如，规律里“或没有离婚”这一条对应 的只有一名顾客。

判断一个算法在新数据上表现好坏的唯一度量，就是在测试集上的评估。然而从直觉上 看 3 ，我们认为简单的模型对新数据的泛化能力更好。如果规律是“年龄大于 50 岁的人想 要买船”，并且这可以解释所有顾客的行为，那么我们将更相信这条规律，而不是与年 龄、子女和婚姻状况都有关系的那条规律。因此，我们总想找到最简单的模型。构建一 个对现有信息量来说过于复杂的模型，正如我们的新手数据科学家做的那样，这被称为 过拟合（overfitting）。如果你在拟合模型时过分关注训练集的细节，得到了一个在训练 集上表现很好、但不能泛化到新数据上的模型，那么就存在过拟合。与之相反，如果你 的模型过于简单——比如说，“有房子的人都买船”——那么你可能无法抓住数据的全部 内容以及数据中的变化，你的模型甚至在训练集上的表现就很差。选择过于简单的模型 被称为欠拟合（underfitting）。

我们的模型越复杂，在训练数据上的预测结果就越好。但是，如果我们的模型过于复杂， 我们开始过多关注训练集中每个单独的数据点，模型就不能很好地泛化到新数据上。

二者之间存在一个最佳位置，可以得到最好的泛化性能。这就是我们想要的模型。

图 2-1 给出了过拟合与欠拟合之间的权衡。

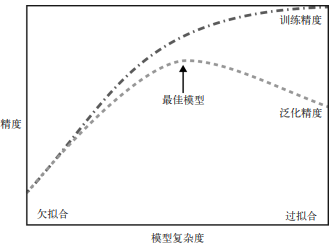
模型复杂度与数据集大小的关系

需要注意，模型复杂度与训练数据集中输入的变化密切相关：数据集中包含的数据点的变 化范围越大，在不发生过拟合的前提下你可以使用的模型就越复杂。通常来说，收集更多 的数据点可以有更大的变化范围，所以更大的数据集可以用来构建更复杂的模型。但是， 仅复制相同的数据点或收集非常相似的数据是无济于事的。

回到前面卖船的例子，如果我们查看了 10 000 多行的顾客数据，并且所有数据都符合 这条规律：“如果顾客年龄大于 45 岁，并且子女少于 3 个或没有离婚，那么他就想要买 船”，那么我们就更有可能相信这是一条有效的规律，比从表 2-1 中仅 12 行数据得出来 的更为可信。

收集更多数据，适当构建更复杂的模型，对监督学习任务往往特别有用。本书主要关注固 定大小的数据集。在现实世界中，你往往能够决定收集多少数据，这可能比模型调参更为 有效。永远不要低估更多数据的力量！

2.3　监督学习算法

现在开始介绍最常用的机器学习算法，并解释这些算法如何从数据中学习以及如何预测。 我们还会讨论每个模型的复杂度如何变化，并概述每个算法如何构建模型。我们将说明每 个算法的优点和缺点，以及它们最适应用于哪类数据。此外还会解释最重要的参数和选项 的含义。4 许多算法都有分类和回归两种形式，两者我们都会讲到。

没有必要通读每个算法的详细描述，但理解模型可以让你更好地理解机器学习算法的各种 工作原理。本章还可以用作参考指南，当你不确定某个算法的工作原理时，就可以回来查 看本章内容。

2.3.1　一些样本数据集

我们将使用一些数据集来说明不同的算法。其中一些数据集很小，而且是模拟的，其目的 是强调算法的某个特定方面。其他数据集都是现实世界的大型数据集。

一个模拟的二分类数据集示例是 forge 数据集，它有两个特征。下列代码将绘制一个散点 图（图 2-2），将此数据集的所有数据点可视化。图像以第一个特征为 x 轴，第二个特征为 y 轴。正如其他散点图那样，每个数据点对应图像中的一点。每个点的颜色和形状对应其 类别：

In[2]:
# 生成数据集
X, y = mglearn.datasets.make_forge()
# 数据集绘图
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.legend(["Class 0", "Class 1"], loc=4)
plt.xlabel("First feature")
plt.ylabel("Second feature")
print("X.shape: {}".format(X.shape))

Out[2]:
X.shape: (26, 2)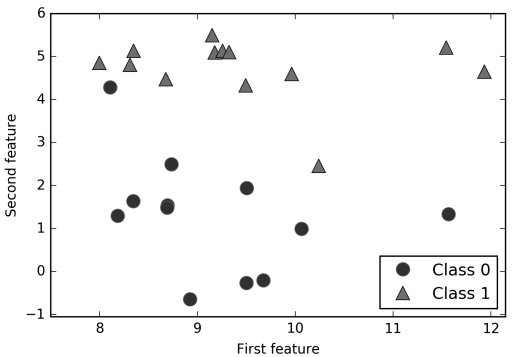

图 2-2：forge 数据集的散点图

从 X.shape 可以看出，这个数据集包含 26 个数据点和 2 个特征。

我们用模拟的 wave 数据集来说明回归算法。wave 数据集只有一个输入特征和一个连续的 目标变量（或响应），后者是模型想要预测的对象。下面绘制的图像（图 2-3）中单一特征 位于 x 轴，回归目标（输出）位于 y 轴：

In[3]:
X, y = mglearn.datasets.make_wave(n_samples=40)
plt.plot(X, y, 'o')
plt.ylim(-3, 3)
plt.xlabel("Feature")
plt.ylabel("Target")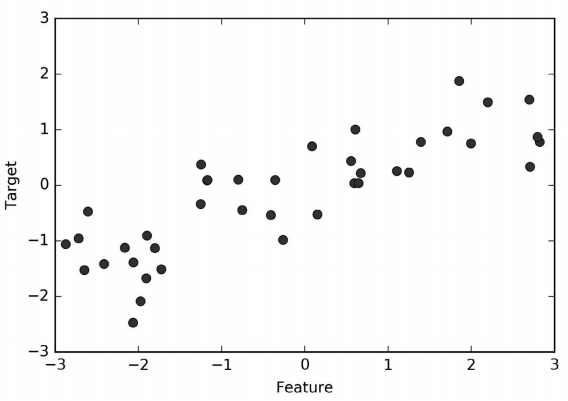

图 2-3：wave 数据集的图像，x 轴表示特征，y 轴表示回归目标

我们之所以使用这些非常简单的低维数据集，是因为它们的可视化非常简单——书页只有 两个维度，所以很难展示特征数超过两个的数据。从特征较少的数据集（也叫低维数据 集）中得出的结论可能并不适用于特征较多的数据集（也叫高维数据集）。只要你记住这 一点，那么在低维数据集上研究算法也是很有启发的。

除了上面这些小型的模拟的数据集，我们还将补充两个现实世界中的数据集，它们都包含 在 scikit-learn 中。其中一个是威斯康星州乳腺癌数据集（简称 cancer），里面记录了乳 腺癌肿瘤的临床测量数据。每个肿瘤都被标记为“良性”（benign，表示无害肿瘤）或“恶 性”（malignant，表示癌性肿瘤），其任务是基于人体组织的测量数据来学习预测肿瘤是否 为恶性。

可以用 scikit-learn 模块的 load_breast_cancer 函数来加载数据：

In[4]:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys(): \n{}".format(cancer.keys()))

Out[4]:
cancer.keys():
dict_keys(['feature_names', 'data', 'DESCR', 'target', 'target_names'])

包含在 scikit-learn 中的数据集通常被保存为 Bunch 对象，里面包含真实 数据以及一些数据集信息。关于 Bunch 对象，你只需要知道它与字典很相 似，而且还有一个额外的好处，就是你可以用点操作符来访问对象的值（比 如用 bunch.key 来代替 bunch['key']）。

这个数据集共包含 569 个数据点，每个数据点有 30 个特征：

In[5]:
print("Shape of cancer data: {}".format(cancer.data.shape))

Out[5]:
Shape of cancer data: (569, 30)

在 569 个数据点中，212 个被标记为恶性，357 个被标记为良性：

In[6]:
print("Sample counts per class:\n{}".format(
 {n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))}))

Out[6]:
Sample counts per class:
{'benign': 357, 'malignant': 212}

为了得到每个特征的语义说明，我们可以看一下 feature_names 属性：

In[7]:
print("Feature names:\n{}".format(cancer.feature_names))

Out[7]:
Feature names:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']

感兴趣的话，你可以阅读 cancer.DESCR 来了解数据的更多信息。

我们还会用到一个现实世界中的回归数据集，即波士顿房价数据集。与这个数据集相关的 任务是，利用犯罪率、是否邻近查尔斯河、公路可达性等信息，来预测 20 世纪 70 年代波 士顿地区房屋价格的中位数。这个数据集包含 506 个数据点和 13 个特征：

In[8]:
from sklearn.datasets import load_boston
boston = load_boston()
print("Data shape: {}".format(boston.data.shape))

Out[8]:
Data shape: (506, 13)

同样，你可以阅读 boston 对象的 DESCR 属性来了解数据集的更多信息。对于我们的目的而言，我们需要扩展这个数据集，输入特征不仅包括这 13 个测量结果，还包括这些特征之间的乘积（也叫交互项）。换句话说，我们不仅将犯罪率和公路可达性作为特征，还将 犯罪率和公路可达性的乘积作为特征。像这样包含导出特征的方法叫作特征工程（feature engineering），将在第 4 章中详细讲述。这个导出的数据集可以用 load_extended_boston 函数加载：

In[9]:
X, y = mglearn.datasets.load_extended_boston()
print("X.shape: {}".format(X.shape))

Out[9]:
X.shape: (506, 104)

最初的 13 个特征加上这 13 个特征两两组合（有放回）得到的 91 个特征，一共有 104 个 特征。

我们将利用这些数据集对不同机器学习算法的性质进行解释说明。但目前来说，先来看算 法本身。首先重新学习上一章见过的 k 近邻（k-NN）算法。

2.3.2 k近邻

k-NN 算法可以说是最简单的机器学习算法。构建模型只需要保存训练数据集即可。想要 对新数据点做出预测，算法会在训练数据集中找到最近的数据点，也就是它的“最近邻”。

1. k近邻分类

k-NN 算法最简单的版本只考虑一个最近邻，也就是与我们想要预测的数据点最近的训练 数据点。预测结果就是这个训练数据点的已知输出。图 2-4 给出了这种分类方法在 forge 数据集上的应用：

In[10]:
mglearn.plots.plot_knn_classification(n_neighbors=1)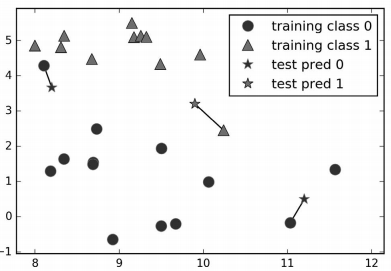

图 2-4：单一最近邻模型对 forge 数据集的预测结果

这里我们添加了 3 个新数据点（用五角星表示）。对于每个新数据点，我们标记了训练集 中与它最近的点。单一最近邻算法的预测结果就是那个点的标签（对应五角星的颜色）。

除了仅考虑最近邻，我还可以考虑任意个（k 个）邻居。这也是 k 近邻算法名字的来历。 在考虑多于一个邻居的情况时，我们用“投票法”（voting）来指定标签。也就是说，对 于每个测试点，我们数一数多少个邻居属于类别 0，多少个邻居属于类别 1。然后将出现 次数更多的类别（也就是 k 个近邻中占多数的类别）作为预测结果。下面的例子（图 2-5） 用到了 3 个近邻：

In[11]:
mglearn.plots.plot_knn_classification(n_neighbors=3)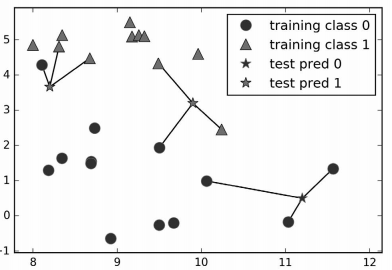

图 2-5：3 近邻模型对 forge 数据集的预测结果

和上面一样，预测结果可以从五角星的颜色看出。你可以发现，左上角新数据点的预测结 果与只用一个邻居时的预测结果不同。

虽然这张图对应的是一个二分类问题，但方法同样适用于多分类的数据集。对于多分类问 题，我们数一数每个类别分别有多少个邻居，然后将最常见的类别作为预测结果。

现在看一下如何通过 scikit-learn 来应用 k 近邻算法。首先，正如第 1 章所述，将数据分 为训练集和测试集，以便评估泛化性能：

In[12]:
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

然后，导入类并将其实例化。这时可以设定参数，比如邻居的个数。这里我们将其设为 3：

In[13]:
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)

现在，利用训练集对这个分类器进行拟合。对于 KNeighborsClassifier 来说就是保存数据 集，以便在预测时计算与邻居之间的距离：

In[14]:
clf.fit(X_train, y_train)

调用 predict 方法来对测试数据进行预测。对于测试集中的每个数据点，都要计算它在训 练集的最近邻，然后找出其中出现次数最多的类别：

In[15]:
print("Test set predictions: {}".format(clf.predict(X_test)))

Out[15]:
Test set predictions: [1 0 1 0 1 0 0]

为了评估模型的泛化能力好坏，我们可以对测试数据和测试标签调用 score 方法：

In[16]:
print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))

Out[16]:
Test set accuracy: 0.86

可以看到，我们的模型精度约为 86%，也就是说，在测试数据集中，模型对其中 86% 的 样本预测的类别都是正确的。

2. 分析KNeighborsClassifier

对于二维数据集，我们还可以在 xy 平面上画出所有可能的测试点的预测结果。我们根据 平面中每个点所属的类别对平面进行着色。这样可以查看决策边界（decision boundary）， 即算法对类别 0 和类别 1 的分界线。

下列代码分别将 1 个、3 个和 9 个邻居三种情况的决策边界可视化，见图 2-6：

In[17]:
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([1, 3, 9], axes):
 # fit方法返回对象本身，所以我们可以将实例化和拟合放在一行代码中
 clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
 mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
 mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
 ax.set_title("{} neighbor(s)".format(n_neighbors))
 ax.set_xlabel("feature 0")
 ax.set_ylabel("feature 1")
axes[0].legend(loc=3)

图 2-6：不同 n_neighbors 值的 k 近邻模型的决策边界

从左图可以看出，使用单一邻居绘制的决策边界紧跟着训练数据。随着邻居个数越来越 多，决策边界也越来越平滑。更平滑的边界对应更简单的模型。换句话说，使用更少的邻 居对应更高的模型复杂度（如图 2-1 右侧所示），而使用更多的邻居对应更低的模型复杂度 （如图 2-1 左侧所示）。假如考虑极端情况，即邻居个数等于训练集中所有数据点的个数， 那么每个测试点的邻居都完全相同（即所有训练点），所有预测结果也完全相同（即训练 集中出现次数最多的类别）。

我们来研究一下能否证实之前讨论过的模型复杂度和泛化能力之间的关系。我们将在现实 世界的乳腺癌数据集上进行研究。先将数据集分成训练集和测试集，然后用不同的邻居个 数对训练集和测试集的性能进行评估。输出结果见图 2-7：

In[18]:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, stratify=cancer.target, random_state=66)
training_accuracy = []
test_accuracy = []
# n_neighbors取值从1到10
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
# 构建模型
 clf = KNeighborsClassifier(n_neighbors=n_neighbors)
 clf.fit(X_train, y_train)
 # 记录训练集精度
 training_accuracy.append(clf.score(X_train, y_train))
 # 记录泛化精度
 test_accuracy.append(clf.score(X_test, y_test))
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()

图像的 x 轴是 n_neighbors，y 轴是训练集精度和测试集精度。虽然现实世界的图像很少有 非常平滑的，但我们仍可以看出过拟合与欠拟合的一些特征（注意，由于更少的邻居对应 更复杂的模型，所以此图相对于图 2-1 做了水平翻转）。仅考虑单一近邻时，训练集上的预 测结果十分完美。但随着邻居个数的增多，模型变得更简单，训练集精度也随之下降。单 一邻居时的测试集精度比使用更多邻居时要低，这表示单一近邻的模型过于复杂。与之相 反，当考虑 10 个邻居时，模型又过于简单，性能甚至变得更差。最佳性能在中间的某处， 邻居个数大约为 6。不过最好记住这张图的坐标轴刻度。最差的性能约为 88% 的精度，这 个结果仍然可以接受。

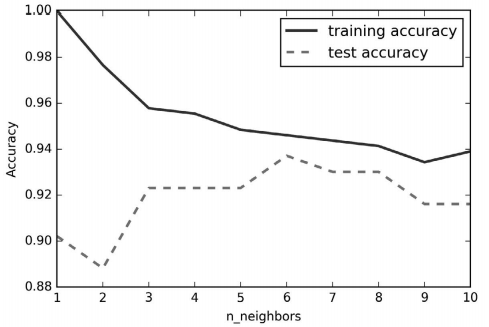
图 2-7：以 n_neighbors 为自变量，对比训练集精度和测试集精度

3. k近邻回归

k 近邻算法还可以用于回归。我们还是先从单一近邻开始，这次使用 wave 数据集。我们添 加了 3 个测试数据点，在 x 轴上用绿色五角星表示。利用单一邻居的预测结果就是最近邻 的目标值。在图 2-8 中用蓝色五角星表示：

In[19]:
mglearn.plots.plot_knn_regression(n_neighbors=1)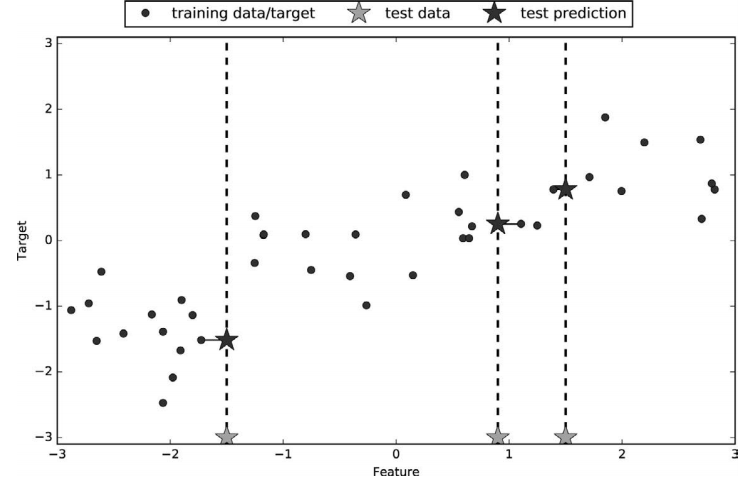

图 2-8：单一近邻回归对 wave 数据集的预测结果

同样，也可以用多个近邻进行回归。在使用多个近邻时，预测结果为这些邻居的平均值 （图 2-9）：

In[20]:
mglearn.plots.plot_knn_regression(n_neighbors=3)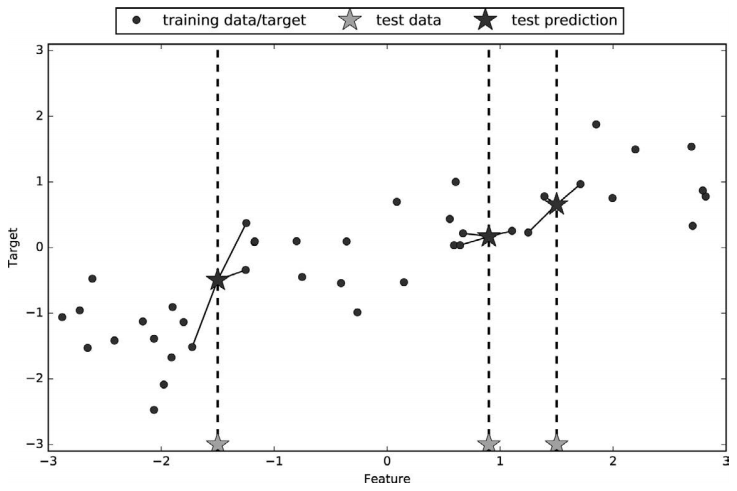

图 2-9：3 个近邻回归对 wave 数据集的预测结果

用于回归的 k 近邻算法在 scikit-learn 的 KNeighborsRegressor 类中实现。其用法与 KNeighborsClassifier 类似：

In[21]:
from sklearn.neighbors import KNeighborsRegressor
X, y = mglearn.datasets.make_wave(n_samples=40)
# 将wave数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 模型实例化，并将邻居个数设为3
reg = KNeighborsRegressor(n_neighbors=3)
# 利用训练数据和训练目标值来拟合模型
reg.fit(X_train, y_train)

现在可以对测试集进行预测：

In[22]:
print("Test set predictions:\n{}".format(reg.predict(X_test)))

Out[22]:
Test set predictions:
[-0.054 0.357 1.137 -1.894 -1.139 -1.631 0.357 0.912 -0.447 -1.139]

我们还可以用 score 方法来评估模型，对于回归问题，这一方法返回的是 R2 分数。R2 分 数也叫作决定系数，是回归模型预测的优度度量，位于 0 到 1 之间。R2 等于 1 对应完美预 测，R2 等于 0 对应常数模型，即总是预测训练集响应（y_train）的平均值：

In[23]:
print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test)))

Out[23]:
Test set R^2: 0.83

这里的分数是 0.83，表示模型的拟合相对较好。

4. 分析KNeighborsRegressor

对于我们的一维数据集，可以查看所有特征取值对应的预测结果（图 2-10）。为了便于绘 图，我们创建一个由许多点组成的测试数据集：

In[24]:
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 创建1000个数据点，在-3和3之间均匀分布
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
 # 利用1个、3个或9个邻居分别进行预测
 reg = KNeighborsRegressor(n_neighbors=n_neighbors)
 reg.fit(X_train, y_train)
 ax.plot(line, reg.predict(line))
 ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
 ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
  ax.set_title(
 "{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(
 n_neighbors, reg.score(X_train, y_train),
 reg.score(X_test, y_test)))
 ax.set_xlabel("Feature")
 ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target",
 "Test data/target"], loc="best")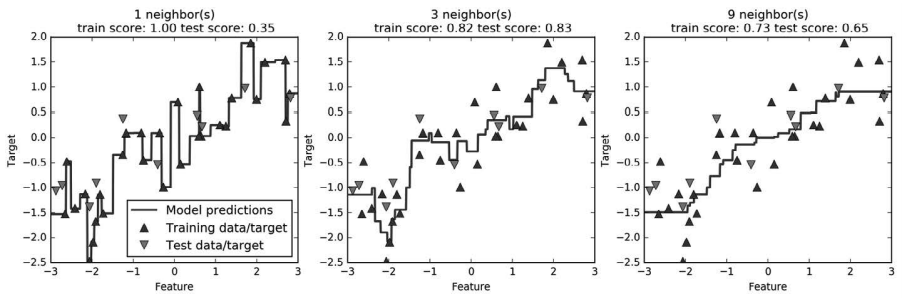

图 2-10：不同 n_neighbors 值的 k 近邻回归的预测结果对比

从图中可以看出，仅使用单一邻居，训练集中的每个点都对预测结果有显著影响，预测结 果的图像经过所有数据点。这导致预测结果非常不稳定。考虑更多的邻居之后，预测结果 变得更加平滑，但对训练数据的拟合也不好。

5. 优点、缺点和参数

一般来说，KNeighbors 分类器有 2 个重要参数：邻居个数与数据点之间距离的度量方法。 在实践中，使用较小的邻居个数（比如 3 个或 5 个）往往可以得到比较好的结果，但你应 该调节这个参数。选择合适的距离度量方法超出了本书的范围。默认使用欧式距离，它在 许多情况下的效果都很好。

k-NN 的优点之一就是模型很容易理解，通常不需要过多调节就可以得到不错的性能。在 考虑使用更高级的技术之前，尝试此算法是一种很好的基准方法。构建最近邻模型的速度 通常很快，但如果训练集很大（特征数很多或者样本数很大），预测速度可能会比较慢。 使用 k-NN 算法时，对数据进行预处理是很重要的（见第 3 章）。这一算法对于有很多特 征（几百或更多）的数据集往往效果不好，对于大多数特征的大多数取值都为 0 的数据集 （所谓的稀疏数据集）来说，这一算法的效果尤其不好。

虽然 k 近邻算法很容易理解，但由于预测速度慢且不能处理具有很多特征的数据集，所以 在实践中往往不会用到。下面介绍的这种方法就没有这两个缺点。

2.3.3　线性模型

线性模型是在实践中广泛使用的一类模型，几十年来被广泛研究，它可以追溯到一百多年 前。线性模型利用输入特征的线性函数（linear function）进行预测，稍后会对此进行解释。

1. 用于回归的线性模型

对于回归问题，线性模型预测的一般公式如下：

ŷ = w[0] * x[0] + w[1] * x[1] + … + w[p] * x[p] + b

这里 x[0] 到 x[p] 表示单个数据点的特征（本例中特征个数为 p+1），w 和 b 是学习模型的 参数，ŷ 是模型的预测结果。对于单一特征的数据集，公式如下：

ŷ = w[0] * x[0] + b

你可能还记得，这就是高中数学里的直线方程。这里 w[0] 是斜率，b 是 y 轴偏移。对于有 更多特征的数据集，w 包含沿每个特征坐标轴的斜率。或者，你也可以将预测的响应值看 作输入特征的加权求和，权重由 w 的元素给出（可以取负值）。

下列代码可以在一维 wave 数据集上学习参数 w[0] 和 b：

In[25]:
mglearn.plots.plot_linear_regression_wave()

Out[25]:
w[0]: 0.393906 b: -0.031804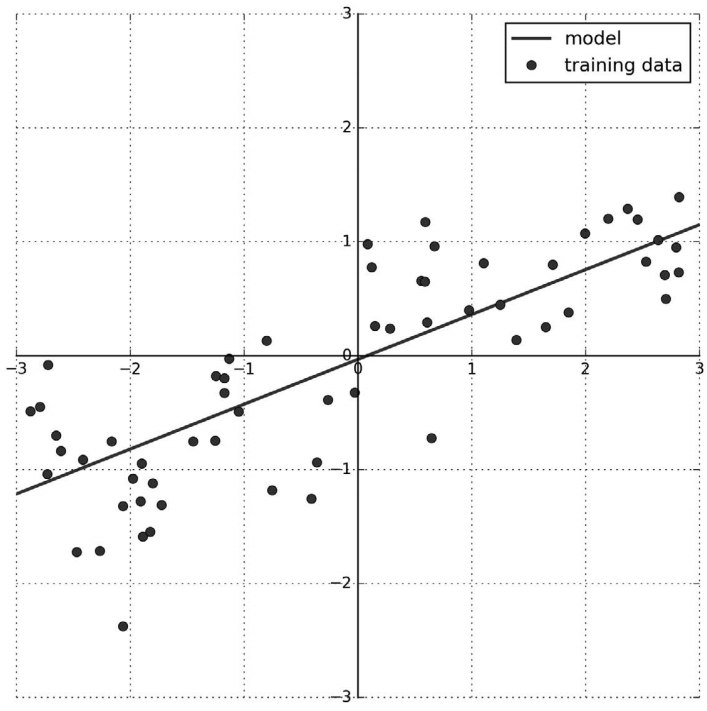

图 2-11：线性模型对 wave 数据集的预测结果

我们在图中添加了坐标网格，便于理解直线的含义。从 w[0] 可以看出，斜率应该在 0.4 左 右，在图像中也可以直观地确认这一点。截距是指预测直线与 y 轴的交点：比 0 略小，也 可以在图像中确认。

用于回归的线性模型可以表示为这样的回归模型：对单一特征的预测结果是一条直线，两 个特征时是一个平面，或者在更高维度（即更多特征）时是一个超平面。

如果将直线的预测结果与图 2-10 中 KNeighborsRegressor 的预测结果进行比较，你会发现 直线的预测能力非常受限。似乎数据的所有细节都丢失了。从某种意义上来说，这种说法 是正确的。假设目标 y 是特征的线性组合，这是一个非常强的（也有点不现实的）假设。 但观察一维数据得出的观点有些片面。对于有多个特征的数据集而言，线性模型可以非常 强大。特别地，如果特征数量大于训练数据点的数量，任何目标 y 都可以（在训练集上） 用线性函数完美拟合 。

有许多不同的线性回归模型。这些模型之间的区别在于如何从训练数据中学习参数 w 和 b，以及如何控制模型复杂度。下面介绍最常见的线性回归模型。

2. 线性回归（又名普通最小二乘法）

线性回归，或者普通最小二乘法（ordinary least squares，OLS），是回归问题最简单也最经 典的线性方法。线性回归寻找参数 w 和 b，使得对训练集的预测值与真实的回归目标值 y 之间的均方误差最小。均方误差（mean squared error）是预测值与真实值之差的平方和除 以样本数。线性回归没有参数，这是一个优点，但也因此无法控制模型的复杂度。

下列代码可以生成图 2-11 中的模型：

In[26]:
from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
lr = LinearRegression().fit(X_train, y_train)

“斜率”参数（w，也叫作权重或系数）被保存在 coef 属性中，而偏移或截距（b）被保 存在 intercept 属性中：

In[27]:
print("lr.coef_: {}".format(lr.coef_))
print("lr.intercept_: {}".format(lr.intercept_))

Out[27]:
lr.coef_: [ 0.394]
lr.intercept_: -0.031804343026759746

你可能注意到了 coef 和 intercept 结尾处奇怪的下划线。scikit-learn 总是将从训练数据中得出的值保存在以下划线结尾的属性中。这是为了将其 与用户设置的参数区分开。

intercept 属性是一个浮点数，而 coef 属性是一个 NumPy 数组，每个元素对应一个输 入特征。由于 wave 数据集中只有一个输入特征，所以 lr.coef_ 中只有一个元素。

我们来看一下训练集和测试集的性能：

In[28]:
print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))

Out[28]:
Training set score: 0.67
Test set score: 0.66

R2 约为 0.66，这个结果不是很好，但我们可以看到，训练集和测试集上的分数非常接近。 这说明可能存在欠拟合，而不是过拟合。对于这个一维数据集来说，过拟合的风险很小， 因为模型非常简单（或受限）。然而，对于更高维的数据集（即有大量特征的数据集），线 性模型将变得更加强大，过拟合的可能性也会变大。我们来看一下 LinearRegression 在更 复杂的数据集上的表现，比如波士顿房价数据集。记住，这个数据集有 506 个样本和 105 个导出特征。首先，加载数据集并将其分为训练集和测试集。然后像前面一样构建线性回 归模型：

In[29]:
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)

比较一下训练集和测试集的分数就可以发现，我们在训练集上的预测非常准确，但测试集 上的 R2 要低很多：

In[30]:
print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))

Out[30]:
Training set score: 0.95
Test set score: 0.61

训练集和测试集之间的性能差异是过拟合的明显标志，因此我们应该试图找到一个可以控 制复杂度的模型。标准线性回归最常用的替代方法之一就是岭回归（ridge regression），下 面来看一下。

3. 岭回归

岭回归也是一种用于回归的线性模型，因此它的预测公式与普通最小二乘法相同。但在岭 回归中，对系数（w）的选择不仅要在训练数据上得到好的预测结果，而且还要拟合附加 约束。我们还希望系数尽量小。换句话说，w 的所有元素都应接近于 0。直观上来看，这 意味着每个特征对输出的影响应尽可能小（即斜率很小），同时仍给出很好的预测结果。 这种约束是所谓正则化（regularization）的一个例子。正则化是指对模型做显式约束，以避免过拟合。岭回归用到的这种被称为 L2 正则化。

岭回归在 linear_model.Ridge 中实现。来看一下它对扩展的波士顿房价数据集的效 果如何：

In[31]:
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test)))

Out[31]:
Training set score: 0.89
Test set score: 0.75

可以看出，Ridge 在训练集上的分数要低于 LinearRegression，但在测试集上的分数更高。 这和我们的预期一致。线性回归对数据存在过拟合。Ridge 是一种约束更强的模型，所以 更不容易过拟合。复杂度更小的模型意味着在训练集上的性能更差，但泛化性能更好。由 于我们只对泛化性能感兴趣，所以应该选择 Ridge 模型而不是 LinearRegression 模型。

Ridge 模型在模型的简单性（系数都接近于 0）与训练集性能之间做出权衡。简单性和训练 集性能二者对于模型的重要程度可以由用户通过设置 alpha 参数来指定。在前面的例子中， 我们用的是默认参数 alpha=1.0。但没有理由认为这会给出最佳权衡。alpha 的最佳设定 值取决于用到的具体数据集。增大 alpha 会使得系数更加趋向于 0，从而降低训练集性能， 但可能会提高泛化性能。例如：

In[32]:
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test)))

Out[32]:
Training set score: 0.79
Test set score: 0.64

减小 alpha 可以让系数受到的限制更小，即在图 2-1 中向右移动。对于非常小的 alpha 值， 系数几乎没有受到限制，我们得到一个与 LinearRegression 类似的模型：

In[33]:
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge01.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge01.score(X_test, y_test)))

Out[33]:
Training set score: 0.93
Test set score: 0.77

这里 alpha=0.1 似乎效果不错。我们可以尝试进一步减小 alpha 以提高泛化性能。现在，注 意参数 alpha 与图 2-1 中的模型复杂度的对应关系。第 5 章将会讨论选择参数的正确方法。

我们还可以查看 alpha 取不同值时模型的 coef 属性，从而更加定性地理解 alpha 参数是 如何改变模型的。更大的 alpha 表示约束更强的模型，所以我们预计大 alpha 对应的 coef 元素比小 alpha 对应的 coef_ 元素要小。这一点可以在图 2-12 中得到证实：

In[34]:
plt.plot(ridge.coef_, 's', label="Ridge alpha=1")
plt.plot(ridge10.coef_, '^', label="Ridge alpha=10")
plt.plot(ridge01.coef_, 'v', label="Ridge alpha=0.1")
plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()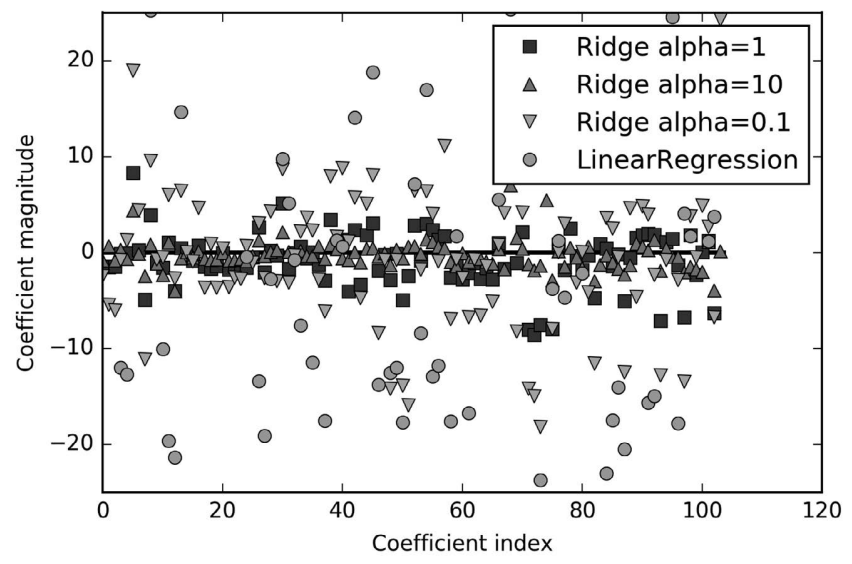

图 2-12：不同 alpha 值的岭回归与线性回归的系数比较

这里 x 轴对应 coef_ 的元素：x=0 对应第一个特征的系数，x=1 对应第二个特征的系数，以 此类推，一直到 x=100。y 轴表示该系数的具体数值。这里需要记住的是，对于 alpha=10， 系数大多在 -3 和 3 之间。对于 alpha=1 的 Ridge 模型，系数要稍大一点。对于 alpha=0.1， 点的范围更大。对于没有做正则化的线性回归（即 alpha=0），点的范围很大，许多点都超 出了图像的范围。

还有一种方法可以用来理解正则化的影响，就是固定 alpha 值，但改变训练数据量。对于图 2-13 来说，我们对波士顿房价数据集做二次抽样，并在数据量逐渐增加的子数据集上分 别对 LinearRegression 和 Ridge(alpha=1) 两个模型进行评估（将模型性能作为数据集大小 的函数进行绘图，这样的图像叫作学习曲线）：

In[35]:
mglearn.plots.plot_ridge_n_samples()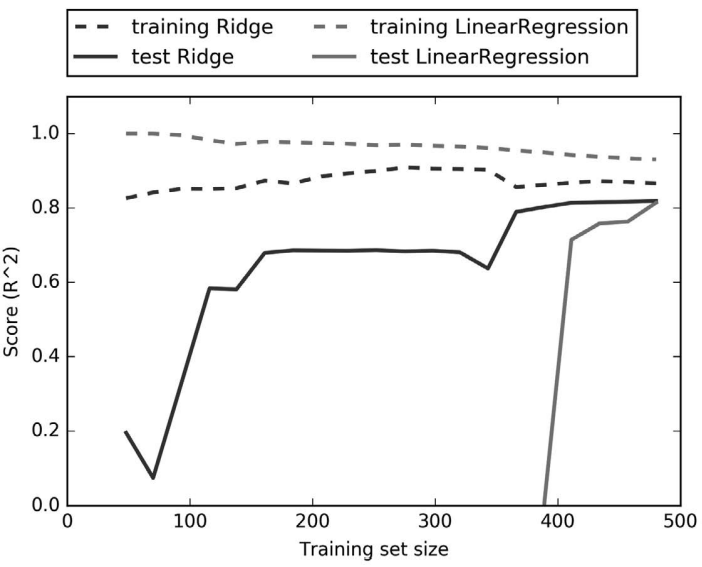

图 2-13：岭回归和线性回归在波士顿房价数据集上的学习曲线

正如所预计的那样，无论是岭回归还是线性回归，所有数据集大小对应的训练分数都要高 于测试分数。由于岭回归是正则化的，因此它的训练分数要整体低于线性回归的训练分 数。但岭回归的测试分数要更高，特别是对较小的子数据集。如果少于 400 个数据点，线 性回归学不到任何内容。随着模型可用的数据越来越多，两个模型的性能都在提升，最终 线性回归的性能追上了岭回归。这里要记住的是，如果有足够多的训练数据，正则化变得 不那么重要，并且岭回归和线性回归将具有相同的性能（在这个例子中，二者相同恰好发 生在整个数据集的情况下，这只是一个巧合）。图 2-13 中还有一个有趣之处，就是线性回 归的训练性能在下降。如果添加更多数据，模型将更加难以过拟合或记住所有的数据。

4. lasso

除了 Ridge，还有一种正则化的线性回归是 Lasso。与岭回归相同，使用 lasso 也是约束系 数使其接近于 0，但用到的方法不同，叫作 L1 正则化。8 L1 正则化的结果是，使用 lasso 时 某些系数刚好为 0。这说明某些特征被模型完全忽略。这可以看作是一种自动化的特征选 择。某些系数刚好为 0，这样模型更容易解释，也可以呈现模型最重要的特征。

我们将 lasso 应用在扩展的波士顿房价数据集上：

In[36]:
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ != 0)))

Out[36]:
Training set score: 0.29
Test set score: 0.21
Number of features used: 4

如你所见，Lasso 在训练集与测试集上的表现都很差。这表示存在欠拟合，我们发现模型 只用到了 105 个特征中的 4 个。与 Ridge 类似，Lasso 也有一个正则化参数 alpha，可以控 制系数趋向于 0 的强度。在上一个例子中，我们用的是默认值 alpha=1.0。为了降低欠拟 合，我们尝试减小 alpha。这么做的同时，我们还需要增加 max_iter 的值（运行迭代的最 大次数）：

In[37]:
# 我们增大max_iter的值，否则模型会警告我们，说应该增大max_iter
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso001.coef_ != 0)))

Out[37]:
Training set score: 0.90
Test set score: 0.77
Number of features used: 33

alpha 值变小，我们可以拟合一个更复杂的模型，在训练集和测试集上的表现也更好。模 型性能比使用 Ridge 时略好一点，而且我们只用到了 105 个特征中的 33 个。这样模型可能 更容易理解。

但如果把 alpha 设得太小，那么就会消除正则化的效果，并出现过拟合，得到与 LinearRegression 类似的结果：

In[38]:
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso00001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso00001.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso00001.coef_ != 0)))

Out[38]:
Training set score: 0.95
Test set score: 0.64
Number of features used: 94

再次像图 2-12 那样对不同模型的系数进行作图，见图 2-14：

In[39]:
plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001")
plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")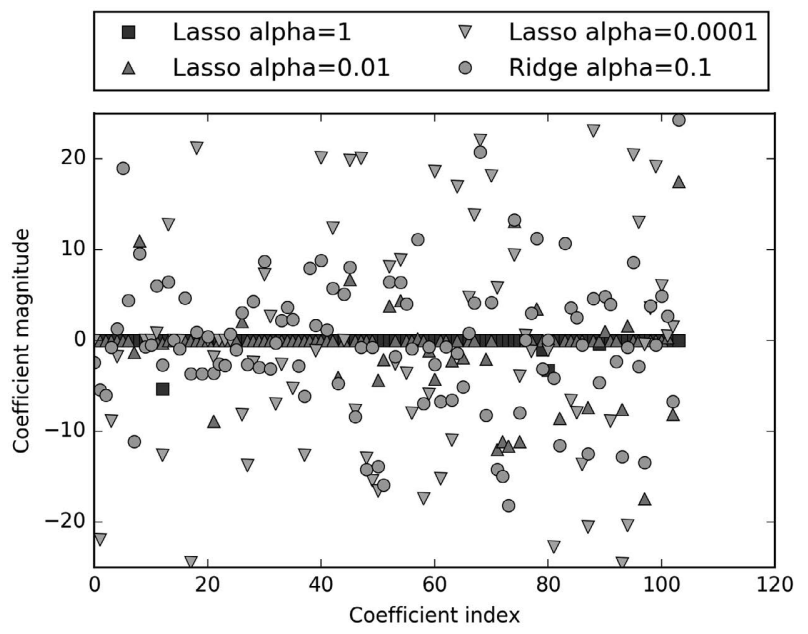

图 2-14：不同 alpha 值的 lasso 回归与岭回归的系数比较

在 alpha=1 时，我们发现不仅大部分系数都是 0（我们已经知道这一点），而且其他系 数也都很小。将 alpha 减小至 0.01，我们得到图中向上的三角形，大部分特征等于 0。 alpha=0.0001 时，我们得到正则化很弱的模型，大部分系数都不为 0，并且还很大。为 了便于比较，图中用圆形表示 Ridge 的最佳结果。alpha=0.1 的 Ridge 模型的预测性能与 alpha=0.01 的 Lasso 模型类似，但 Ridge 模型的所有系数都不为 0。

在实践中，在两个模型中一般首选岭回归。但如果特征很多，你认为只有其中几个是重要 的，那么选择 Lasso 可能更好。同样，如果你想要一个容易解释的模型，Lasso 可以给出 更容易理解的模型，因为它只选择了一部分输入特征。scikit-learn 还提供了 ElasticNet 类，结合了 Lasso 和 Ridge 的惩罚项。在实践中，这种结合的效果最好，不过代价是要调 节两个参数：一个用于 L1 正则化，一个用于 L2 正则化。

5. 用于分类的线性模型

线性模型也广泛应用于分类问题。我们首先来看二分类。这时可以利用下面的公式进行 预测：

ŷ = w[0] * x[0] + w[1] * x[1] + …+ w[p] * x[p] + b > 0

这个公式看起来与线性回归的公式非常相似，但我们没有返回特征的加权求和，而是为预 测设置了阈值（0）。如果函数值小于 0，我们就预测类别 -1；如果函数值大于 0，我们就 预测类别 +1。对于所有用于分类的线性模型，这个预测规则都是通用的。同样，有很多种 不同的方法来找出系数（w）和截距（b）。

对于用于回归的线性模型，输出 ŷ 是特征的线性函数，是直线、平面或超平面（对于更高 维的数据集）。对于用于分类的线性模型，决策边界是输入的线性函数。换句话说，（二 元）线性分类器是利用直线、平面或超平面来分开两个类别的分类器。本节我们将看到这 方面的例子。

学习线性模型有很多种算法。这些算法的区别在于以下两点：

• 系数和截距的特定组合对训练数据拟合好坏的度量方法；
• 是否使用正则化，以及使用哪种正则化方法。

不同的算法使用不同的方法来度量“对训练集拟合好坏”。由于数学上的技术原因，不可 能调节 w 和 b 使得算法产生的误分类数量最少。对于我们的目的，以及对于许多应用而 言，上面第一点（称为损失函数）的选择并不重要。

最常见的两种线性分类算法是 Logistic 回归（logistic regression）和线性支持向量机（linear support vector machine，线性 SVM），前者在 linear_model.LogisticRegression 中实现， 后者在 svm.LinearSVC（SVC 代表支持向量分类器）中实现。虽然 LogisticRegression 的名字中含有回归（regression），但它是一种分类算法，并不是回归算法，不应与 LinearRegression 混淆。

我们可以将 LogisticRegression 和 LinearSVC 模型应用到 forge 数据集上，并将线性模型 找到的决策边界可视化（图 2-15）：

In[40]:
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X, y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
 clf = model.fit(X, y)
 mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5,
 ax=ax, alpha=.7)
 mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
 ax.set_title("{}".format(clf.__class__.__name__))
 ax.set_xlabel("Feature 0")
 ax.set_ylabel("Feature 1")
axes[0].legend()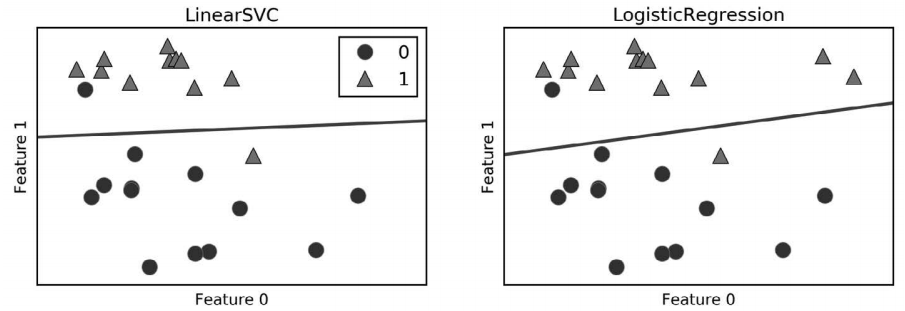

图 2-15：线性 SVM 和 Logistic 回归在 forge 数据集上的决策边界（均为默认参数）

在这张图中，forge 数据集的第一个特征位于 x 轴，第二个特征位于 y 轴，与前面相同。 图中分别展示了 LinearSVC 和 LogisticRegression 得到的决策边界，都是直线，将顶部归 为类别 1 的区域和底部归为类别 0 的区域分开了。换句话说，对于每个分类器而言，位于 黑线上方的新数据点都会被划为类别 1，而在黑线下方的点都会被划为类别 0。

两个模型得到了相似的决策边界。注意，两个模型中都有两个点的分类是错误的。两个模 型都默认使用 L2 正则化，就像 Ridge 对回归所做的那样。

对于 LogisticRegression 和 LinearSVC，决定正则化强度的权衡参数叫作 C。C 值越 大，对应的正则化越弱。换句话说，如果参数 C 值较大，那么 LogisticRegression 和 LinearSVC 将尽可能将训练集拟合到最好，而如果 C 值较小，那么模型更强调使系数向量 （w）接近于 0。

参数 C 的作用还有另一个有趣之处。较小的 C 值可以让算法尽量适应“大多数”数据点， 而较大的 C 值更强调每个数据点都分类正确的重要性。下面是使用 LinearSVC 的图示 （图 2-16）：

In[41]:
mglearn.plots.plot_linear_svc_regularization()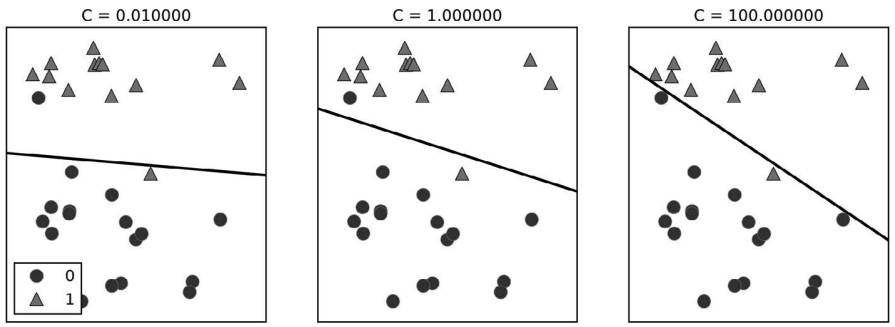

图 2-16：不同 C 值的线性 SVM 在 forge 数据集上的决策边界

在左侧的图中，C 值很小，对应强正则化。大部分属于类别 0 的点都位于底部，大部分属 于类别 1 的点都位于顶部。强正则化的模型会选择一条相对水平的线，有两个点分类错 误。在中间的图中，C 值稍大，模型更关注两个分类错误的样本，使决策边界的斜率变大。 最后，在右侧的图中，模型的 C 值非常大，使得决策边界的斜率也很大，现在模型对类 别 0 中所有点的分类都是正确的。类别 1 中仍有一个点分类错误，这是因为对这个数据集 来说，不可能用一条直线将所有点都分类正确。右侧图中的模型尽量使所有点的分类都正 确，但可能无法掌握类别的整体分布。换句话说，这个模型很可能过拟合。

与回归的情况类似，用于分类的线性模型在低维空间中看起来可能非常受限，决策边界只 能是直线或平面。同样，在高维空间中，用于分类的线性模型变得非常强大，当考虑更多 特征时，避免过拟合变得越来越重要。

我们在乳腺癌数据集上详细分析 LogisticRegression：

In[42]:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, stratify=cancer.target, random_state=42)
logreg = LogisticRegression().fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg.score(X_train, y_train)))
print("Test set score: {:.3f}".format(logreg.score(X_test, y_test)))

Out[42]:
Training set score: 0.953
Test set score: 0.958

C=1 的默认值给出了相当好的性能，在训练集和测试集上都达到 95% 的精度。但由于训练 集和测试集的性能非常接近，所以模型很可能是欠拟合的。我们尝试增大 C 来拟合一个更 灵活的模型：

In[43]:
logreg100 = LogisticRegression(C=100).fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg100.score(X_train, y_train)))
print("Test set score: {:.3f}".format(logreg100.score(X_test, y_test)))

Out[43]:
Training set score: 0.972
Test set score: 0.965

使用 C=100 可以得到更高的训练集精度，也得到了稍高的测试集精度，这也证实了我们的 直觉，即更复杂的模型应该性能更好。

我们还可以研究使用正则化更强的模型时会发生什么。设置 C=0.01：

In[44]:
logreg001 = LogisticRegression(C=0.01).fit(X_train, y_train)
print("Training set score: {:.3f}".format(logreg001.score(X_train, y_train)))
print("Test set score: {:.3f}".format(logreg001.score(X_test, y_test)))

Out[44]:
Training set score: 0.934
Test set score: 0.930

正如我们所料，在图 2-1 中将已经欠拟合的模型继续向左移动，训练集和测试集的精度都 比采用默认参数时更小。

最后，来看一下正则化参数 C 取三个不同的值时模型学到的系数（图 2-17）：

In[45]:
plt.plot(logreg.coef_.T, 'o', label="C=1")
plt.plot(logreg100.coef_.T, '^', label="C=100")
plt.plot(logreg001.coef_.T, 'v', label="C=0.001")
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0, 0, cancer.data.shape[1])
plt.ylim(-5, 5)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.legend()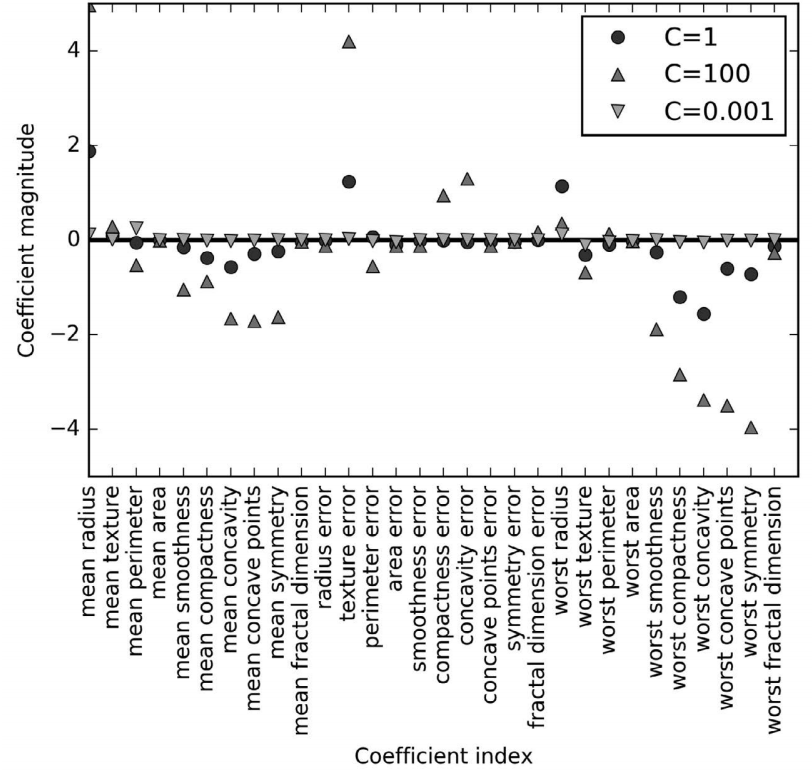

图 2-17：不同 C 值的 Logistic 回归在乳腺癌数据集上学到的系数

由于 LogisticRegression 默认应用 L2 正则化，所以其结果与图 2-12 中 Ridge 的结果类似。更强的正则化使得系数更趋向于 0，但系数永远不会正 好等于 0。进一步观察图像，还可以在第 3 个系数那里发现有趣之处，这个 系数是“平均周长”（mean perimeter）。C=100 和 C=1 时，这个系数为负，而 C=0.001 时这个系数为正，其绝对值比 C=1 时还要大。在解释这样的模型时， 人们可能会认为，系数可以告诉我们某个特征与哪个类别有关。例如，人 们可能会认为高“纹理错误”（texture error）特征与“恶性”样本有关。但 “平均周长”系数的正负号发生变化，说明较大的“平均周长”可以被当作 “良性”的指标或“恶性”的指标，具体取决于我们考虑的是哪个模型。这 也说明，对线性模型系数的解释应该始终持保留态度。

如果想要一个可解释性更强的模型，使用 L1 正则化可能更好，因为它约束模型只使用少 数几个特征。下面是使用 L1 正则化的系数图像和分类精度（图 2-18）。

图 2-18：对于不同的 C 值，L1 惩罚的 Logistic 回归在乳腺癌数据集上学到的系数

In[46]:
for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']):
 lr_l1 = LogisticRegression(C=C, penalty="l1").fit(X_train, y_train)
 print("Training accuracy of l1 logreg with C={:.3f}: {:.2f}".format(
 C, lr_l1.score(X_train, y_train)))
 print("Test accuracy of l1 logreg with C={:.3f}: {:.2f}".format(
 C, lr_l1.score(X_test, y_test)))
plt.plot(lr_l1.coef_.T, marker, label="C={:.3f}".format(C))
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0, 0, cancer.data.shape[1])
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.ylim(-5, 5)
plt.legend(loc=3)

Out[46]:
Training accuracy of l1 logreg with C=0.001: 0.91
Test accuracy of l1 logreg with C=0.001: 0.92
Training accuracy of l1 logreg with C=1.000: 0.96
Test accuracy of l1 logreg with C=1.000: 0.96
Training accuracy of l1 logreg with C=100.000: 0.99
Test accuracy of l1 logreg with C=100.000: 0.98

如你所见，用于二分类的线性模型与用于回归的线性模型有许多相似之处。与用于回归的 线性模型一样，模型的主要差别在于 penalty 参数，这个参数会影响正则化，也会影响模 型是使用所有可用特征还是只选择特征的一个子集。

6. 用于多分类的线性模型

许多线性分类模型只适用于二分类问题，不能轻易推广到多类别问题（除了 Logistic 回 归）。将二分类算法推广到多分类算法的一种常见方法是“一对其余”（one-vs.-rest）方 法。在“一对其余”方法中，对每个类别都学习一个二分类模型，将这个类别与所有其 他类别尽量分开，这样就生成了与类别个数一样多的二分类模型。在测试点上运行所有 二类分类器来进行预测。在对应类别上分数最高的分类器“胜出”，将这个类别标签返回 作为预测结果。

每个类别都对应一个二类分类器，这样每个类别也都有一个系数（w）向量和一个截距 （b）。下面给出的是分类置信方程，其结果中最大值对应的类别即为预测的类别标签：

w[0] * x[0] + w[1] * x[1] + … + w[p] * x[p] + b

多分类 Logistic 回归背后的数学与“一对其余”方法稍有不同，但它也是对每个类别都有 一个系数向量和一个截距，也使用了相同的预测方法。

我们将“一对其余”方法应用在一个简单的三分类数据集上。我们用到了一个二维数据 集，每个类别的数据都是从一个高斯分布中采样得出的（见图 2-19）：

In[47]:
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])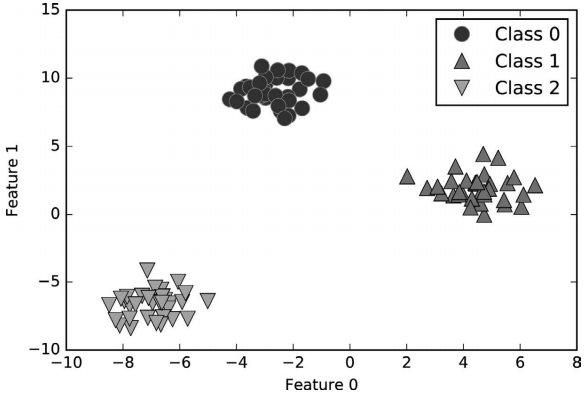

图 2-19：包含 3 个类别的二维玩具数据集

现在，在这个数据集上训练一个 LinearSVC 分类器：

In[48]:
linear_svm = LinearSVC().fit(X, y)
print("Coefficient shape: ", linear_svm.coef_.shape)
print("Intercept shape: ", linear_svm.intercept_.shape)

Out[48]:
Coefficient shape: (3, 2)
Intercept shape: (3,)

我们看到，coef 的形状是 (3, 2)，说明 coef 每行包含三个类别之一的系数向量，每列 包含某个特征（这个数据集有 2 个特征）对应的系数值。现在 intercept_ 是一维数组，保 存每个类别的截距。

我们将这 3 个二类分类器给出的直线可视化（图 2-20）：

In[49]:
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
 ['b', 'r', 'g']):
 plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
 'Line class 2'], loc=(1.01, 0.3))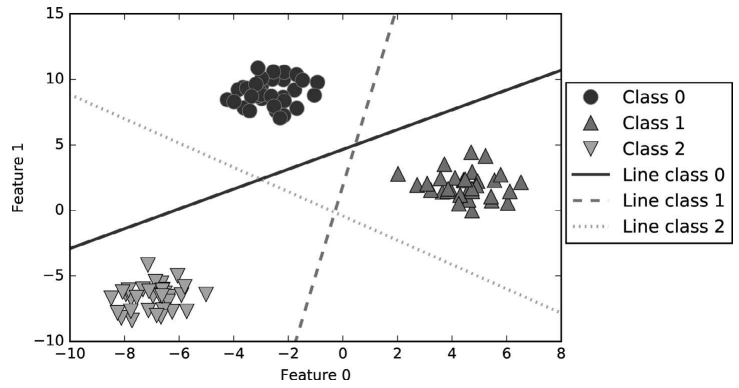

图 2-20：三个“一对其余”分类器学到的决策边界

你可以看到，训练集中所有属于类别 0 的点都在与类别 0 对应的直线上方，这说明它们位 于这个二类分类器属于“类别 0”的那一侧。属于类别 0 的点位于与类别 2 对应的直线上 方，这说明它们被类别 2 的二类分类器划为“其余”。属于类别 0 的点位于与类别 1 对应 的直线左侧，这说明类别 1 的二元分类器将它们划为“其余”。因此，这一区域的所有点 都会被最终分类器划为类别 0（类别 0 的分类器的分类置信方程的结果大于 0，其他两个 类别对应的结果都小于 0）。

但图像中间的三角形区域属于哪一个类别呢，3 个二类分类器都将这一区域内的点划为 “其余”。这里的点应该划归到哪一个类别呢？答案是分类方程结果最大的那个类别，即最 接近的那条线对应的类别。

下面的例子（图 2-21）给出了二维空间中所有区域的预测结果：

In[50]:
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
 ['b', 'r', 'g']):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
 'Line class 2'], loc=(1.01, 0.3))
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")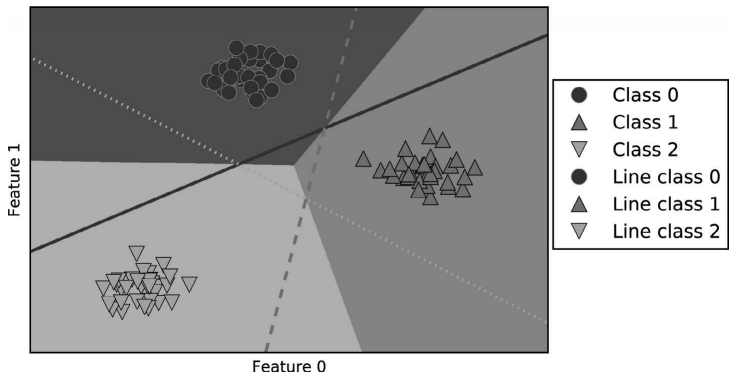

图 2-21：三个“一对其余”分类器得到的多分类决策边界

7. 优点、缺点和参数

线性模型的主要参数是正则化参数，在回归模型中叫作 alpha，在 LinearSVC 和 LogisticRegression 中叫作 C。alpha 值较大或 C 值较小，说明模型比较简单。特别是对于回归模型 而言，调节这些参数非常重要。通常在对数尺度上对 C 和 alpha 进行搜索。你还需要确定 的是用 L1 正则化还是 L2 正则化。如果你假定只有几个特征是真正重要的，那么你应该用 L1 正则化，否则应默认使用 L2 正则化。如果模型的可解释性很重要的话，使用 L1 也会 有帮助。由于 L1 只用到几个特征，所以更容易解释哪些特征对模型是重要的，以及这些 特征的作用。

线性模型的训练速度非常快，预测速度也很快。这种模型可以推广到非常大的数据集，对 稀疏数据也很有效。如果你的数据包含数十万甚至上百万个样本，你可能需要研究如何使 用 LogisticRegression 和 Ridge 模型的 solver='sag' 选项，在处理大型数据时，这一选项 比默认值要更快。其他选项还有 SGDClassifier 类和 SGDRegressor 类，它们对本节介绍的 线性模型实现了可扩展性更强的版本。

线性模型的另一个优点在于，利用我们之间见过的用于回归和分类的公式，理解如何进 行预测是相对比较容易的。不幸的是，往往并不完全清楚系数为什么是这样的。如果你 的数据集中包含高度相关的特征，这一问题尤为突出。在这种情况下，可能很难对系数 做出解释。

如果特征数量大于样本数量，线性模型的表现通常都很好。它也常用于非常大的数据集， 只是因为训练其他模型并不可行。但在更低维的空间中，其他模型的泛化性能可能更好。 2.3.7 节会介绍几个线性模型不适用的例子。

方法链

scikit-learn 中所有模型的 fit 方法返回的都是 self。这允许你像下面这样编写代码 （我们在本章已经用过很多次了）：

In[51]:
# 用一行代码初始化模型并拟合
logreg = LogisticRegression().fit(X_train, y_train)

这里我们利用 fit 的返回值（即 self）将训练后的模型赋值给变量 logreg。这种方 法调用的拼接（先调用 init，然后调用 fit）被称为方法链（method chaining）。 scikit-learn 中方法链的另一个常见用法是在一行代码中同时 fit 和 predict：

In[52]:
logreg = LogisticRegression()
y_pred = logreg.fit(X_train, y_train).predict(X_test)

最后，你甚至可以在一行代码中完成模型初始化、拟合和预测：

In[53]:
y_pred = LogisticRegression().fit(X_train, y_train).predict(X_test)

不过这种非常简短的写法并不完美。一行代码中发生了很多事情，可能会使代码变得 难以阅读。此外，拟合后的回归模型也没有保存在任何变量中，所以我们既不能查看 它也不能用它来预测其他数据。

2.3.4　朴素贝叶斯分类器

朴素贝叶斯分类器是与上一节介绍的线性模型非常相似的一种分类器，但它的训练速度往 往更快。这种高效率所付出的代价是，朴素贝叶斯模型的泛化能力要比线性分类器（如 LogisticRegression 和 LinearSVC）稍差。

朴素贝叶斯模型如此高效的原因在于，它通过单独查看每个特征来学习参数，并从每 个特征中收集简单的类别统计数据。scikit-learn 中实现了三种朴素贝叶斯分类器： GaussianNB、BernoulliNB 和 MultinomialNB。GaussianNB 可 应 用 于 任 意 连 续 数 据， 而 BernoulliNB 假定输入数据为二分类数据，MultinomialNB 假定输入数据为计数数据（即每 个特征代表某个对象的整数计数，比如一个单词在句子里出现的次数）。BernoulliNB 和 MultinomialNB 主要用于文本数据分类。

BernoulliNB 分类器计算每个类别中每个特征不为 0 的元素个数。用一个例子来说明会很 容易理解：

In[54]:
X = np.array([[0, 1, 0, 1],
 [1, 0, 1, 1],
 [0, 0, 0, 1],
 [1, 0, 1, 0]])
y = np.array([0, 1, 0, 1])

这里我们有 4 个数据点，每个点有 4 个二分类特征。一共有两个类别：0 和 1。对于类别 0 （第 1、3 个数据点），第一个特征有 2 个为零、0 个不为零，第二个特征有 1 个为零、1 个 不为零，以此类推。然后对类别 1 中的数据点计算相同的计数。计算每个类别中的非零元 素个数，大体上看起来像这样：

In[55]:
counts = {}
for label in np.unique(y):
 # 对每个类别进行遍历
 # 计算（求和）每个特征中1的个数
 counts[label] = X[y == label].sum(axis=0)
print("Feature counts:\n{}".format(counts))

Out[55]:
Feature counts:
{0: array([0, 1, 0, 2]), 1: array([2, 0, 2, 1])}

另外两种朴素贝叶斯模型（MultinomialNB 和 GaussianNB）计算的统计数据类型略有不同。 MultinomialNB 计算每个类别中每个特征的平均值，而 GaussianNB 会保存每个类别中每个 特征的平均值和标准差。

要想做出预测，需要将数据点与每个类别的统计数据进行比较，并将最匹配的类别作为预 测结果。有趣的是，MultinomialNB 和 BernoulliNB 预测公式的形式都与线性模型完全相同 （见 2.3.3 节）。不幸的是，朴素贝叶斯模型 coef 的含义与线性模型稍有不同，因为 coef 不同于 w。

优点、缺点和参数

MultinomialNB 和 BernoulliNB 都只有一个参数 alpha，用于控制模型复杂度。alpha 的工作 原理是，算法向数据中添加 alpha 这么多的虚拟数据点，这些点对所有特征都取正值。这 可以将统计数据“平滑化”（smoothing）。alpha 越大，平滑化越强，模型复杂度就越低。 算法性能对 alpha 值的鲁棒性相对较好，也就是说，alpha 值对模型性能并不重要。但调 整这个参数通常都会使精度略有提高。

GaussianNB 主要用于高维数据，而另外两种朴素贝叶斯模型则广泛用于稀疏计数数据，比 如文本。MultinomialNB 的性能通常要优于 BernoulliNB，特别是在包含很多非零特征的数 据集（即大型文档）上。

朴素贝叶斯模型的许多优点和缺点都与线性模型相同。它的训练和预测速度都很快，训练 过程也很容易理解。该模型对高维稀疏数据的效果很好，对参数的鲁棒性也相对较好。朴 素贝叶斯模型是很好的基准模型，常用于非常大的数据集，在这些数据集上即使训练线性 模型可能也要花费大量时间。

2.3.5　决策树

决策树是广泛用于分类和回归任务的模型。本质上，它从一层层的 if/else 问题中进行学 习，并得出结论。

这些问题类似于你在“20 Questions”游戏 9 中可能会问的问题。想象一下，你想要区分下 面这四种动物：熊、鹰、企鹅和海豚。你的目标是通过提出尽可能少的 if/else 问题来得到 正确答案。你可能首先会问：这种动物有没有羽毛，这个问题会将可能的动物减少到只有 两种。如果答案是“有”，你可以问下一个问题，帮你区分鹰和企鹅。例如，你可以问这 种动物会不会飞。如果这种动物没有羽毛，那么可能是海豚或熊，所以你需要问一个问题 来区分这两种动物——比如问这种动物有没有鳍。

这一系列问题可以表示为一棵决策树，如图 2-22 所示。

In[56]:
mglearn.plots.plot_animal_tree()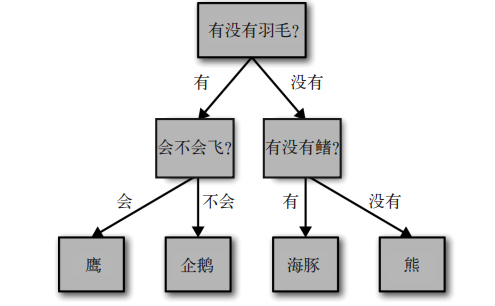

图 2-22：区分几种动物的决策树

在这张图中，树的每个结点代表一个问题或一个包含答案的终结点（也叫叶结点）。树的 边将问题的答案与将问的下一个问题连接起来。

用机器学习的语言来说就是，为了区分四类动物（鹰、企鹅、海豚和熊），我们利用三个 特征（“有没有羽毛”“会不会飞”和“有没有鳍”）来构建一个模型。我们可以利用监督 学习从数据中学习模型，而无需人为构建模型。

1. 构造决策树

我们在图 2-23 所示的二维分类数据集上构造决策树。这个数据集由 2 个半月形组成，每个 类别都包含 50 个数据点。我们将这个数据集称为 two_moons。

学习决策树，就是学习一系列 if/else 问题，使我们能够以最快的速度得到正确答案。在机器 学习中，这些问题叫作测试（不要与测试集弄混，测试集是用来测试模型泛化性能的数据）。 数据通常并不是像动物的例子那样具有二元特征（是 / 否）的形式，而是表示为连续特征， 比如图 2-23 所示的二维数据集。用于连续数据的测试形式是：“特征 i 的值是否大于 a ？”

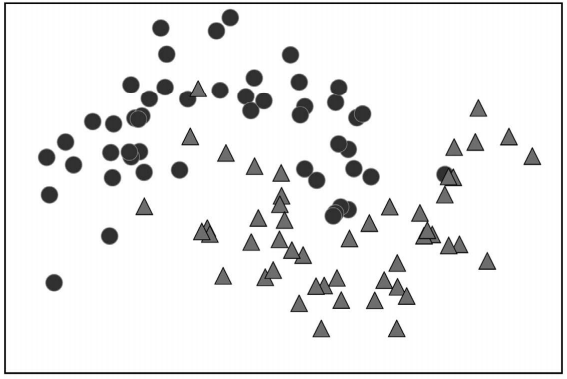
图 2-23：用于构造决策树的 two_moons 数据集

为了构造决策树，算法搜遍所有可能的测试，找出对目标变量来说信息量最大的那一个。 图 2-24 展示了选出的第一个测试。将数据集在 x[1]=0.0596 处垂直划分可以得到最多信 息，它在最大程度上将类别 0 中的点与类别 1 中的点进行区分。顶结点（也叫根结点）表 示整个数据集，包含属于类别 0 的 50 个点和属于类别 1 的 50 个点。通过测试 x[1] <= 0.0596 的真假来对数据集进行划分，在图中表示为一条黑线。如果测试结果为真，那么将 这个点分配给左结点，左结点里包含属于类别 0 的 2 个点和属于类别 1 的 32 个点。否则 将这个点分配给右结点，右结点里包含属于类别 0 的 48 个点和属于类别 1 的 18 个点。这 两个结点对应于图 2-24 中的顶部区域和底部区域。尽管第一次划分已经对两个类别做了很 好的区分，但底部区域仍包含属于类别 0 的点，顶部区域也仍包含属于类别 1 的点。我们 可以在两个区域中重复寻找最佳测试的过程，从而构建出更准确的模型。图 2-25 展示了信 息量最大的下一次划分，这次划分是基于 x[0] 做出的，分为左右两个区域。

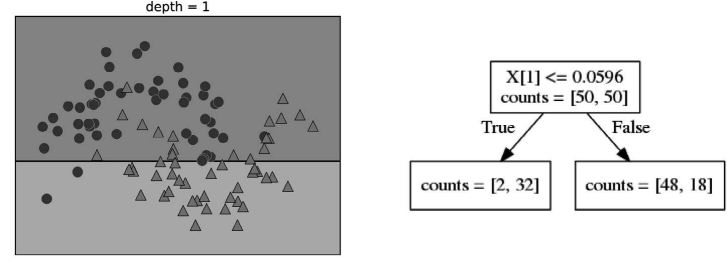
图 2-24：深度为 1 的树的决策边界（左）与相应的树（右）

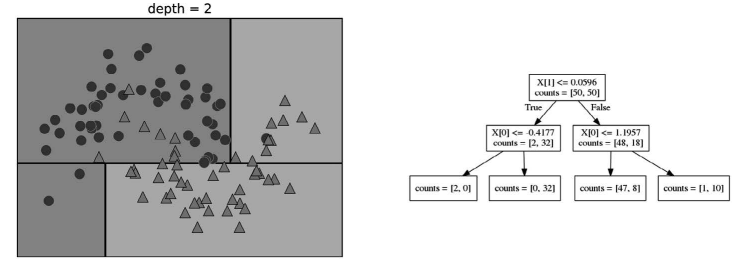
图 2-25：深度为 2 的树的决策边界（左）与相应的树（右）

这一递归过程生成一棵二元决策树，其中每个结点都包含一个测试。或者你可以将每个测 试看成沿着一条轴对当前数据进行划分。这是一种将算法看作分层划分的观点。由于每个 测试仅关注一个特征，所以划分后的区域边界始终与坐标轴平行。

对数据反复进行递归划分，直到划分后的每个区域（决策树的每个叶结点）只包含单一目 标值（单一类别或单一回归值）。如果树中某个叶结点所包含数据点的目标值都相同，那 么这个叶结点就是纯的（pure）。这个数据集的最终划分结果见图 2-26。

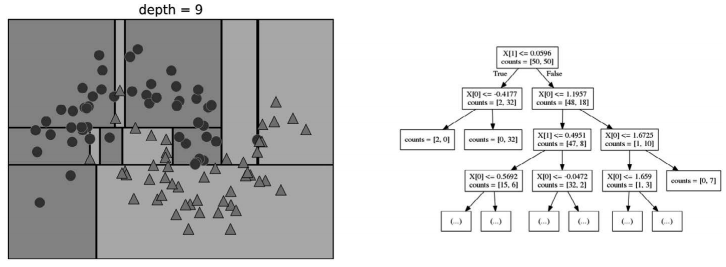
图 2-26：深度为 9 的树的决策边界（左）与相应的树的一部分（右）；完整的决策树非常大，很难可视化

想要对新数据点进行预测，首先要查看这个点位于特征空间划分的哪个区域，然后将该区 域的多数目标值（如果是纯的叶结点，就是单一目标值）作为预测结果。从根结点开始对 树进行遍历就可以找到这一区域，每一步向左还是向右取决于是否满足相应的测试。

决策树也可以用于回归任务，使用的方法完全相同。预测的方法是，基于每个结点的测试 对树进行遍历，最终找到新数据点所属的叶结点。这一数据点的输出即为此叶结点中所有 训练点的平均目标值。

2. 控制决策树的复杂度

通常来说，构造决策树直到所有叶结点都是纯的叶结点，这会导致模型非常复杂，并且对 训练数据高度过拟合。纯叶结点的存在说明这棵树在训练集上的精度是 100%。训练集中 的每个数据点都位于分类正确的叶结点中。在图 2-26 的左图中可以看出过拟合。你可以看 到，在所有属于类别 0 的点中间有一块属于类别 1 的区域。另一方面，有一小条属于类别 0 的区域，包围着最右侧属于类别 0 的那个点。这并不是人们想象中决策边界的样子，这 个决策边界过于关注远离同类别其他点的单个异常点。

防止过拟合有两种常见的策略：一种是及早停止树的生长，也叫预剪枝（pre-pruning）； 另一种是先构造树，但随后删除或折叠信息量很少的结点，也叫后剪枝（post-pruning）或 剪枝（pruning）。预剪枝的限制条件可能包括限制树的最大深度、限制叶结点的最大数目， 或者规定一个结点中数据点的最小数目来防止继续划分。

scikit-learn 的决策树在 DecisionTreeRegressor 类和 DecisionTreeClassifier 类中实现。 scikit-learn 只实现了预剪枝，没有实现后剪枝。

我们在乳腺癌数据集上更详细地看一下预剪枝的效果。和前面一样，我们导入数据集并将 其分为训练集和测试集。然后利用默认设置来构建模型，默认将树完全展开（树不断分 支，直到所有叶结点都是纯的）。我们固定树的 random_state，用于在内部解决平局问题：

In[58]:
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))

Out[58]:
Accuracy on training set: 1.000
Accuracy on test set: 0.937

不出所料，训练集上的精度是 100%，这是因为叶结点都是纯的，树的深度很大，足以完 美地记住训练数据的所有标签。测试集精度比之前讲过的线性模型略低，线性模型的精度 约为 95%。

如果我们不限制决策树的深度，它的深度和复杂度都可以变得特别大。因此，未剪枝的树 容易过拟合，对新数据的泛化性能不佳。现在我们将预剪枝应用在决策树上，这可以在完 美拟合训练数据之前阻止树的展开。一种选择是在到达一定深度后停止树的展开。这里我 们设置 max_depth=4，这意味着只可以连续问 4 个问题（参见图 2-24 和图 2-26）。限制树的 深度可以减少过拟合。这会降低训练集的精度，但可以提高测试集的精度：

In[59]:
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))

Out[59]:
Accuracy on training set: 0.988
Accuracy on test set: 0.951

3. 分析决策树

我们可以利用 tree 模块的 export_graphviz 函数来将树可视化。这个函数会生成一 个 .dot 格式的文件，这是一种用于保存图形的文本文件格式。我们设置为结点添加颜色 的选项，颜色表示每个结点中的多数类别，同时传入类别名称和特征名称，这样可以对 树正确标记：

In[60]:
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["malignant","benign"],
 feature_names=cancer.feature_names, impurity=False, filled=True)

我们可以利用 graphviz 模块读取这个文件并将其可视化（你也可以使用任何能够读取 .dot 文件的程序），见图 2-27：

In[61]:
import graphviz
with open("tree.dot") as f:
 dot_graph = f.read()
graphviz.Source(dot_graph)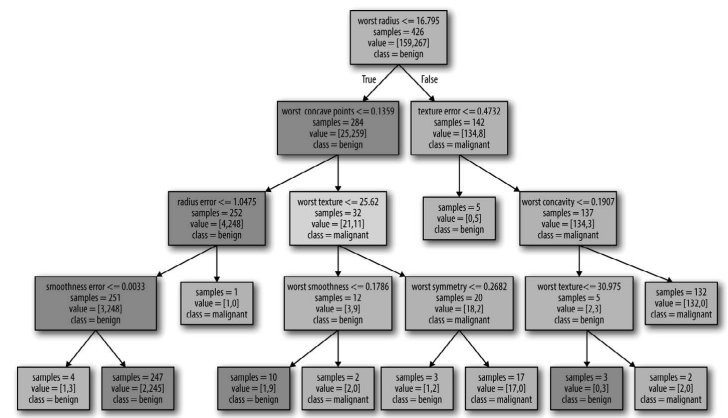

图 2-27：基于乳腺癌数据集构造的决策树的可视化

树的可视化有助于深入理解算法是如何进行预测的，也是易于向非专家解释的机器学习算 法的优秀示例。不过，即使这里树的深度只有 4 层，也有点太大了。深度更大的树（深度 为 10 并不罕见）更加难以理解。一种观察树的方法可能有用，就是找出大部分数据的实 际路径。图 2-27 中每个结点的 samples 给出了该结点中的样本个数，values 给出的是每 个类别的样本个数。观察 worst radius <= 16.795 分支右侧的子结点，我们发现它只包含 8 个良性样本，但有 134 个恶性样本。树的这一侧的其余分支只是利用一些更精细的区别 将这 8 个良性样本分离出来。在第一次划分右侧的 142 个样本中，几乎所有样本（132 个） 最后都进入最右侧的叶结点中。

再来看一下根结点的左侧子结点，对于 worst radius > 16.795，我们得到 25 个恶性样本 和 259 个良性样本。几乎所有良性样本最终都进入左数第二个叶结点中，大部分其他叶结 点都只包含很少的样本。

4. 树的特征重要性

查看整个树可能非常费劲，除此之外，我还可以利用一些有用的属性来总结树的工作原 理。其中最常用的是特征重要性（feature importance），它为每个特征对树的决策的重要性 进行排序。对于每个特征来说，它都是一个介于 0 和 1 之间的数字，其中 0 表示“根本没 用到”，1 表示“完美预测目标值”。特征重要性的求和始终为 1：

In[62]:
print("Feature importances:\n{}".format(tree.feature_importances_))

Out[62]:
Feature importances:
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.01
 0.048 0. 0. 0.002 0. 0. 0. 0. 0. 0.727 0.046
 0. 0. 0.014 0. 0.018 0.122 0.012 0. ]

我们可以将特征重要性可视化，与我们将线性模型的系数可视化的方法类似（图 2-28）：

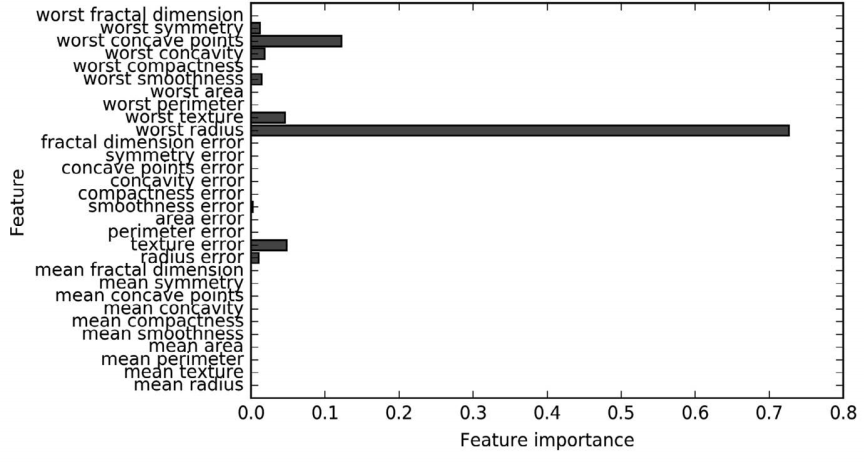
图 2-28：在乳腺癌数据集上学到的决策树的特征重要性

In[63]:
def plot_feature_importances_cancer(model):
 n_features = cancer.data.shape[1]
 plt.barh(range(n_features), model.feature_importances_, align='center')
 plt.yticks(np.arange(n_features), cancer.feature_names)
 plt.xlabel("Feature importance")
 plt.ylabel("Feature")
plot_feature_importances_cancer(tree)

这里我们看到，顶部划分用到的特征（“worst radius”）是最重要的特征。这也证实了我们 在分析树时的观察结论，即第一层划分已经将两个类别区分得很好。

但是，如果某个特征的 featureimportance 很小，并不能说明这个特征没有提供任何信 息。这只能说明该特征没有被树选中，可能是因为另一个特征也包含了同样的信息。

与线性模型的系数不同，特征重要性始终为正数，也不能说明该特征对应哪个类别。特征 重要性告诉我们“worst radius”（最大半径）特征很重要，但并没有告诉我们半径大表示 样本是良性还是恶性。事实上，在特征和类别之间可能没有这样简单的关系，你可以在下 面的例子中看出这一点（图 2-29 和图 2-30）：

In[64]:
tree = mglearn.plots.plot_tree_not_monotone()
display(tree)

Out[64]:
Feature importances: [ 0. 1.]

图 2-29：一个二维数据集（y 轴上的特征与类别标签是非单调的关系）与决策树给出的决策边界

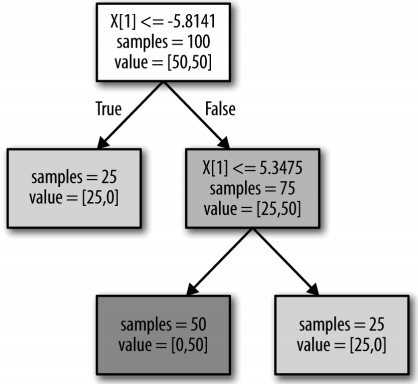
图 2-30：从图 2-29 的数据中学到的决策树

该图显示的是有两个特征和两个类别的数据集。这里所有信息都包含在 X[1] 中，没有用到 X[0]。但 X[1] 和输出类别之间并不是单调关系，即我们不能这么说：“较大的 X[1] 对应类 别 0，较小的 X[1] 对应类别 1”（反之亦然）。

虽然我们主要讨论的是用于分类的决策树，但对用于回归的决策树来说，所有内容都是 类似的，在 DecisionTreeRegressor 中实现。回归树的用法和分析与分类树非常类似。但 在将基于树的模型用于回归时，我们想要指出它的一个特殊性质。DecisionTreeRegressor （以及其他所有基于树的回归模型）不能外推（extrapolate），也不能在训练数据范围之外 进行预测。

我们利用计算机内存（RAM）历史价格的数据集来更详细地研究这一点。图 2-31 给出了 这个数据集的图像，x 轴为日期，y 轴为那一年 1 兆字节（MB）RAM 的价格：

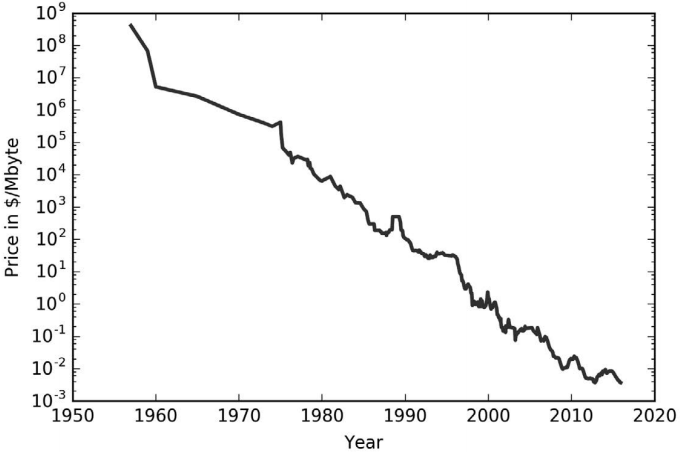
图 2-31：用对数坐标绘制 RAM 价格的历史发展

In[65]:
import pandas as pd
ram_prices = pd.read_csv("data/ram_price.csv")
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("Year")
plt.ylabel("Price in $/Mbyte")

注意 y 轴的对数刻度。在用对数坐标绘图时，二者的线性关系看起来非常好，所以预测应 该相对比较容易，除了一些不平滑之处之外。

我们将利用 2000 年前的历史数据来预测 2000 年后的价格，只用日期作为特征。我们将 对比两个简单的模型：DecisionTreeRegressor 和 LinearRegression。我们对价格取对数， 使得二者关系的线性相对更好。这对 DecisionTreeRegressor 不会产生什么影响，但对 LinearRegression 的影响却很大（我们将在第 4 章中进一步讨论）。训练模型并做出预测之 后，我们应用指数映射来做对数变换的逆运算。为了便于可视化，我们这里对整个数据集 进行预测，但如果是为了定量评估，我们将只考虑测试数据集：

In[66]:
from sklearn.tree import DecisionTreeRegressor
# 利用历史数据预测2000年后的价格
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]
# 基于日期来预测价格
X_train = data_train.date[:, np.newaxis]
# 我们利用对数变换得到数据和目标之间更简单的关系
y_train = np.log(data_train.price)
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)
# 对所有数据进行预测
X_all = ram_prices.date[:, np.newaxis]
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
# 对数变换逆运算
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)

这里创建的图 2-32 将决策树和线性回归模型的预测结果与真实值进行对比：

In[67]:
plt.semilogy(data_train.date, data_train.price, label="Training data")
plt.semilogy(data_test.date, data_test.price, label="Test data")
plt.semilogy(ram_prices.date, price_tree, label="Tree prediction")
plt.semilogy(ram_prices.date, price_lr, label="Linear prediction")
plt.legend()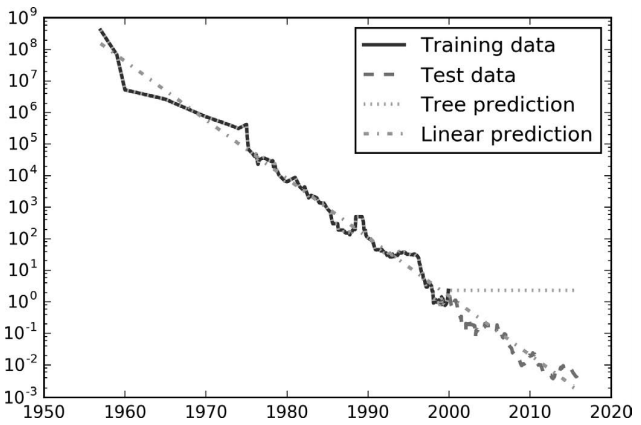

图 2-32：线性模型和回归树对 RAM 价格数据的预测结果对比

两个模型之间的差异非常明显。线性模型用一条直线对数据做近似，这是我们所知道的。 这条线对测试数据（2000 年后的价格）给出了相当好的预测，不过忽略了训练数据和测试 数据中一些更细微的变化。与之相反，树模型完美预测了训练数据。由于我们没有限制树 的复杂度，因此它记住了整个数据集。但是，一旦输入超出了模型训练数据的范围，模型 就只能持续预测最后一个已知数据点。树不能在训练数据的范围之外生成“新的”响应。 所有基于树的模型都有这个缺点。

5. 优点、缺点和参数

如前所述，控制决策树模型复杂度的参数是预剪枝参数，它在树完全展开之前停止树的构 造。通常来说，选择一种预剪枝策略（设置 max_depth、max_leaf_nodes 或 minsamples leaf）足以防止过拟合。

与前面讨论过的许多算法相比，决策树有两个优点：一是得到的模型很容易可视化，非 专家也很容易理解（至少对于较小的树而言）；二是算法完全不受数据缩放的影响。由于 每个特征被单独处理，而且数据的划分也不依赖于缩放，因此决策树算法不需要特征预处 理，比如归一化或标准化。特别是特征的尺度完全不一样时或者二元特征和连续特征同时 存在时，决策树的效果很好。

决策树的主要缺点在于，即使做了预剪枝，它也经常会过拟合，泛化性能很差。因此，在 大多数应用中，往往使用下面介绍的集成方法来替代单棵决策树。

2.3.6　决策树集成

集成（ensemble）是合并多个机器学习模型来构建更强大模型的方法。在机器学习文献 中有许多模型都属于这一类，但已证明有两种集成模型对大量分类和回归的数据集都是有效的，二者都以决策树为基础，分别是随机森林（random forest）和梯度提升决策树 （gradient boosted decision tree）。

1. 随机森林

我们刚刚说过，决策树的一个主要缺点在于经常对训练数据过拟合。随机森林是解决这个 问题的一种方法。随机森林本质上是许多决策树的集合，其中每棵树都和其他树略有不 同。随机森林背后的思想是，每棵树的预测可能都相对较好，但可能对部分数据过拟合。 如果构造很多树，并且每棵树的预测都很好，但都以不同的方式过拟合，那么我们可以对 这些树的结果取平均值来降低过拟合。既能减少过拟合又能保持树的预测能力，这可以在 数学上严格证明。

为了实现这一策略，我们需要构造许多决策树。每棵树都应该对目标值做出可以接受的预 测，还应该与其他树不同。随机森林的名字来自于将随机性添加到树的构造过程中，以确 保每棵树都各不相同。随机森林中树的随机化方法有两种：一种是通过选择用于构造树的 数据点，另一种是通过选择每次划分测试的特征。我们来更深入地研究这一过程。

构造随机森林。 想 要 构 造 一 个 随 机 森 林 模 型， 你 需 要 确 定 用 于 构 造 的 树 的 个 数 （RandomForestRegressor 或 RandomForestClassifier 的 n_estimators 参数）。比如我们想 要构造 10 棵树。这些树在构造时彼此完全独立，算法对每棵树进行不同的随机选择，以 确保树和树之间是有区别的。想要构造一棵树，首先要对数据进行自助采样（bootstrap sample）。也就是说，从 n_samples 个数据点中有放回地（即同一样本可以被多次抽取）重 复随机抽取一个样本，共抽取 n_samples 次。这样会创建一个与原数据集大小相同的数据 集，但有些数据点会缺失（大约三分之一），有些会重复。

举例说明，比如我们想要创建列表 ['a', 'b', 'c', 'd'] 的自助采样。一种可能的自主采 样是 ['b', 'd', 'd', 'c']，另一种可能的采样为 ['d', 'a', 'd', 'a']。

接下来，基于这个新创建的数据集来构造决策树。但是，要对我们在介绍决策树时描述的 算法稍作修改。在每个结点处，算法随机选择特征的一个子集，并对其中一个特征寻找最 佳测试，而不是对每个结点都寻找最佳测试。选择的特征个数由 max_features 参数来控 制。每个结点中特征子集的选择是相互独立的，这样树的每个结点可以使用特征的不同子 集来做出决策。

由于使用了自助采样，随机森林中构造每棵决策树的数据集都是略有不同的。由于每个结 点的特征选择，每棵树中的每次划分都是基于特征的不同子集。这两种方法共同保证随机 森林中所有树都不相同。

在这个过程中的一个关键参数是 max_features。如果我们设置 max_features 等于 n_features，那么每次划分都要考虑数据集的所有特征，在特征选择的过程中没有 添加随机性（不过自助采样依然存在随机性）。如果设置 max_features 等于 1，那 么在划分时将无法选择对哪个特征进行测试，只能对随机选择的某个特征搜索不同 的阈值。因此，如果 max_features 较大，那么随机森林中的树将会十分相似，利 用最独特的特征可以轻松拟合数据。如果 max_features 较小，那么随机森林中的 树将会差异很大，为了很好地拟合数据，每棵树的深度都要很大。

想要利用随机森林进行预测，算法首先对森林中的每棵树进行预测。对于回归问题，我们 可以对这些结果取平均值作为最终预测。对于分类问题，则用到了“软投票”（soft voting） 策略。也就是说，每个算法做出“软”预测，给出每个可能的输出标签的概率。对所有树 的预测概率取平均值，然后将概率最大的类别作为预测结果。

分析随机森林。下面将由 5 棵树组成的随机森林应用到前面研究过的 two_moons 数据集上：

In[68]:
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
 random_state=42)
forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)

作为随机森林的一部分，树被保存在 estimator_ 属性中。我们将每棵树学到的决策边界可 视化，也将它们的总预测（即整个森林做出的预测）可视化（图 2-33）：

In[69]:
fig, axes = plt.subplots(2, 3, figsize=(20, 10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
 ax.set_title("Tree {}".format(i))
 mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax)
mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1],
 alpha=.4)
axes[-1, -1].set_title("Random Forest")
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)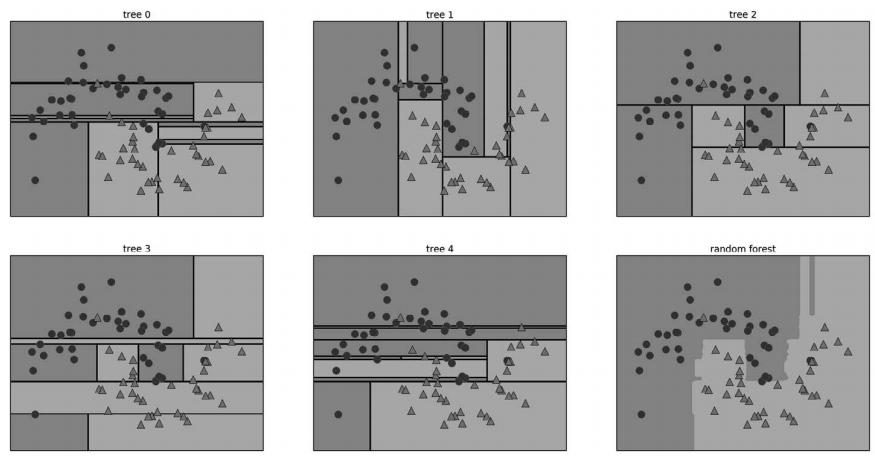

图 2-33：5 棵随机化的决策树找到的决策边界，以及将它们的预测概率取平均后得到的决策边界

你可以清楚地看到，这 5 棵树学到的决策边界大不相同。每棵树都犯了一些错误，因为这 里画出的一些训练点实际上并没有包含在这些树的训练集中，原因在于自助采样。

随机森林比单独每一棵树的过拟合都要小，给出的决策边界也更符合直觉。在任何实际应 用中，我们会用到更多棵树（通常是几百或上千），从而得到更平滑的边界。

再举一个例子，我们将包含 100 棵树的随机森林应用在乳腺癌数据集上：

In[70]:
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, random_state=0)
forest = RandomForestClassifier(n_estimators=100, random_state=0)
forest.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(forest.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(forest.score(X_test, y_test)))

Out[70]:
Accuracy on training set: 1.000
Accuracy on test set: 0.972

在没有调节任何参数的情况下，随机森林的精度为 97%，比线性模型或单棵决策树都要 好。我们可以调节 max_features 参数，或者像单棵决策树那样进行预剪枝。但是，随机森 林的默认参数通常就已经可以给出很好的结果。

与决策树类似，随机森林也可以给出特征重要性，计算方法是将森林中所有树的特征重要 性求和并取平均。一般来说，随机森林给出的特征重要性要比单棵树给出的更为可靠。参 见图 2-34。

In[71]:
plot_feature_importances_cancer(forest)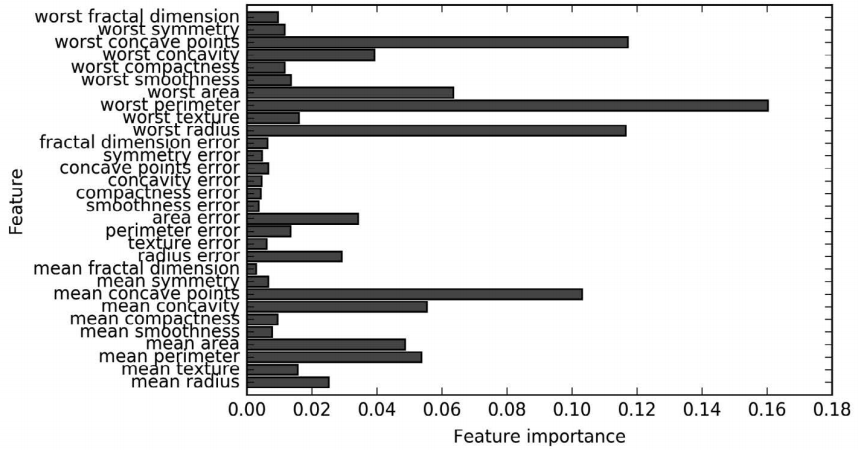

图 2-34：拟合乳腺癌数据集得到的随机森林的特征重要性

如你所见，与单棵树相比，随机森林中有更多特征的重要性不为零。与单棵决策树类似， 随机森林也给了“worst radius”（最大半径）特征很大的重要性，但从总体来看，它实际 上却选择“worst perimeter”（最大周长）作为信息量最大的特征。由于构造随机森林过程 中的随机性，算法需要考虑多种可能的解释，结果就是随机森林比单棵树更能从总体把握 数据的特征。

优点、缺点和参数。用于回归和分类的随机森林是目前应用最广泛的机器学习方法之一。 这种方法非常强大，通常不需要反复调节参数就可以给出很好的结果，也不需要对数据进 行缩放。

从本质上看，随机森林拥有决策树的所有优点，同时弥补了决策树的一些缺陷。仍然使 用决策树的一个原因是需要决策过程的紧凑表示。基本上不可能对几十棵甚至上百棵树 做出详细解释，随机森林中树的深度往往比决策树还要大（因为用到了特征子集）。因 此，如果你需要以可视化的方式向非专家总结预测过程，那么选择单棵决策树可能更好。 虽然在大型数据集上构建随机森林可能比较费时间，但在一台计算机的多个 CPU 内核上 并行计算也很容易。如果你用的是多核处理器（几乎所有的现代化计算机都是），你可 以用 n_jobs 参数来调节使用的内核个数。使用更多的 CPU 内核，可以让速度线性增加 （使用 2 个内核，随机森林的训练速度会加倍），但设置 n_jobs 大于内核个数是没有用 的。你可以设置 n_jobs=-1 来使用计算机的所有内核。

你应该记住，随机森林本质上是随机的，设置不同的随机状态（或者不设置 random_state 参数）可以彻底改变构建的模型。森林中的树越多，它对随机状态选择的鲁棒性就越好。 如果你希望结果可以重现，固定 random_state 是很重要的。

对于维度非常高的稀疏数据（比如文本数据），随机森林的表现往往不是很好。对于这种 数据，使用线性模型可能更合适。即使是非常大的数据集，随机森林的表现通常也很好， 训练过程很容易并行在功能强大的计算机的多个 CPU 内核上。不过，随机森林需要更大 的内存，训练和预测的速度也比线性模型要慢。对一个应用来说，如果时间和内存很重要 的话，那么换用线性模型可能更为明智。

需要调节的重要参数有 n_estimators 和 maxfeatures，可能还包括预剪枝选项（如 max depth）。n_estimators 总是越大越好。对更多的树取平均可以降低过拟合，从而得到鲁棒 性更好的集成。不过收益是递减的，而且树越多需要的内存也越多，训练时间也越长。常 用的经验法则就是“在你的时间 / 内存允许的情况下尽量多”。

前面说过，max_features 决定每棵树的随机性大小，较小的 max_features 可以降低过拟 合。一般来说，好的经验就是使用默认值：对于分类，默认值是 maxfeatures=sqrt(n features)；对于回归，默认值是 max_features=n_features。增大 maxfeatures 或 max leaf_nodes 有时也可以提高性能。它还可以大大降低用于训练和预测的时间和空间要求。

2. 梯度提升回归树（梯度提升机）

梯度提升回归树是另一种集成方法，通过合并多个决策树来构建一个更为强大的模型。虽 然名字中含有“回归”，但这个模型既可以用于回归也可以用于分类。与随机森林方法不 同，梯度提升采用连续的方式构造树，每棵树都试图纠正前一棵树的错误。默认情况下， 梯度提升回归树中没有随机化，而是用到了强预剪枝。梯度提升树通常使用深度很小（1到 5 之间）的树，这样模型占用的内存更少，预测速度也更快。

梯度提升背后的主要思想是合并许多简单的模型（在这个语境中叫作弱学习器），比如深 度较小的树。每棵树只能对部分数据做出好的预测，因此，添加的树越来越多，可以不断 迭代提高性能。

梯度提升树经常是机器学习竞赛的优胜者，并且广泛应用于业界。与随机森林相比，它通 常对参数设置更为敏感，但如果参数设置正确的话，模型精度更高。

除了预剪枝与集成中树的数量之外，梯度提升的另一个重要参数是 learning_rate（学习 率），用于控制每棵树纠正前一棵树的错误的强度。较高的学习率意味着每棵树都可以做 出较强的修正，这样模型更为复杂。通过增大 n_estimators 来向集成中添加更多树，也可 以增加模型复杂度，因为模型有更多机会纠正训练集上的错误。

下面是在乳腺癌数据集上应用 GradientBoostingClassifier 的示例。默认使用 100 棵树， 最大深度是 3，学习率为 0.1：

In[72]:
from sklearn.ensemble import GradientBoostingClassifier
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, random_state=0)
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))

Out[72]:
Accuracy on training set: 1.000
Accuracy on test set: 0.958

由于训练集精度达到 100%，所以很可能存在过拟合。为了降低过拟合，我们可以限制最 大深度来加强预剪枝，也可以降低学习率：

In[73]:
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))

Out[73]:
Accuracy on training set: 0.991
Accuracy on test set: 0.972

In[74]:
gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
gbrt.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(gbrt.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(gbrt.score(X_test, y_test)))

Out[74]:
Accuracy on training set: 0.988
Accuracy on test set: 0.965

降低模型复杂度的两种方法都降低了训练集精度，这和预期相同。在这个例子中，减小树 的最大深度显著提升了模型性能，而降低学习率仅稍稍提高了泛化性能。

对于其他基于决策树的模型，我们也可以将特征重要性可视化，以便更好地理解模型 （图 2-35）。由于我们用到了 100 棵树，所以即使所有树的深度都是 1，查看所有树也是 不现实的：

In[75]:
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
plot_feature_importances_cancer(gbrt)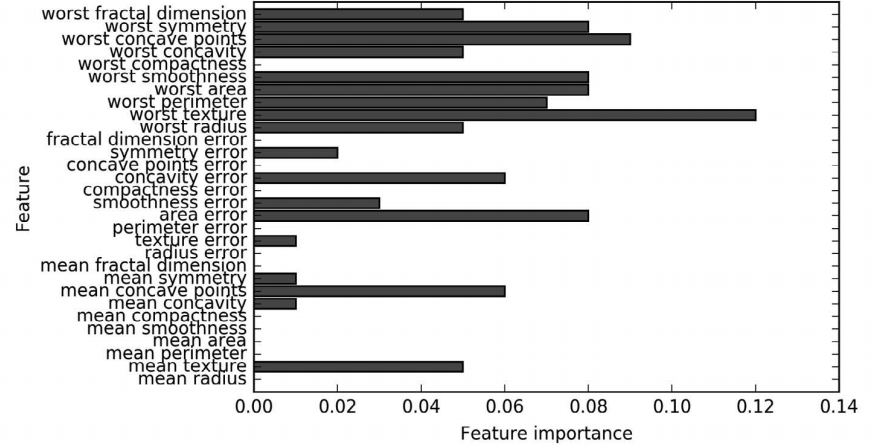

图 2-35：用于拟合乳腺癌数据集的梯度提升分类器给出的特征重要性

可以看到，梯度提升树的特征重要性与随机森林的特征重要性有些类似，不过梯度提升完 全忽略了某些特征。

由于梯度提升和随机森林两种方法在类似的数据上表现得都很好，因此一种常用的方法就 是先尝试随机森林，它的鲁棒性很好。如果随机森林效果很好，但预测时间太长，或者机 器学习模型精度小数点后第二位的提高也很重要，那么切换成梯度提升通常会有用。

如果你想要将梯度提升应用在大规模问题上，可以研究一下 xgboost 包及其 Python 接口， 在写作本书时，这个库在许多数据集上的速度都比 scikit-learn 对梯度提升的实现要快 （有时调参也更简单）。

优点、缺点和参数。梯度提升决策树是监督学习中最强大也最常用的模型之一。其主要缺 点是需要仔细调参，而且训练时间可能会比较长。与其他基于树的模型类似，这一算法不 需要对数据进行缩放就可以表现得很好，而且也适用于二元特征与连续特征同时存在的数 据集。与其他基于树的模型相同，它也通常不适用于高维稀疏数据。

梯度提升树模型的主要参数包括树的数量 n_estimators 和学习率 learningrate，后者 用于控制每棵树对前一棵树的错误的纠正强度。这两个参数高度相关，因为 learning rate 越低，就需要更多的树来构建具有相似复杂度的模型。随机森林的 n_estimators 值 总是越大越好，但梯度提升不同，增大 n_estimators 会导致模型更加复杂，进而可能导 致过拟合。通常的做法是根据时间和内存的预算选择合适的 n_estimators，然后对不同的 learning_rate 进行遍历。

另一个重要参数是 max_depth（或 max_leaf_nodes），用于降低每棵树的复杂度。梯度提升 模型的 max_depth 通常都设置得很小，一般不超过 5。

2.3.7　核支持向量机

我们要讨论的下一种监督学习模型是核支持向量机（kernelized support vector machine）。 在 2.3.3 节中，我们研究了将线性支持向量机用于分类任务。核支持向量机（通常简称为 SVM）是可以推广到更复杂模型的扩展，这些模型无法被输入空间的超平面定义。虽然支 持向量机可以同时用于分类和回归，但我们只会介绍用于分类的情况，它在 SVC 中实现。 类似的概念也适用于支持向量回归，后者在 SVR 中实现。

核支持向量机背后的数学有点复杂，已经超出了本书的范围。你可以阅读 Hastie、 Tibshirani 和 Friedman 合著的《统计学习基础》一书（http://statweb.stanford.edu/~tibs/ElemStatLearn/）的第 12 章了解更多细节。不过，我们会努力向读者传达这一方法背后的理念。

1. 线性模型与非线性特征

如图 2-15 所示，线性模型在低维空间中可能非常受限，因为线和平面的灵活性有限。有一 种方法可以让线性模型更加灵活，就是添加更多的特征——举个例子，添加输入特征的交 互项或多项式。

我们来看一下 2.3.5 节中用到的模拟数据集（见图 2-29）：

In[76]:
X, y = make_blobs(centers=4, random_state=8)
y = y % 2
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")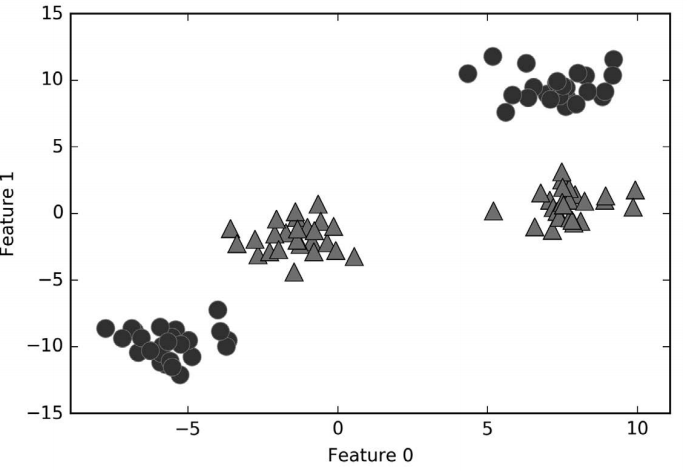

图 2-36：二分类数据集，其类别并不是线性可分的

用于分类的线性模型只能用一条直线来划分数据点，对这个数据集无法给出较好的结果 （见图 2-37）：

In[77]:
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")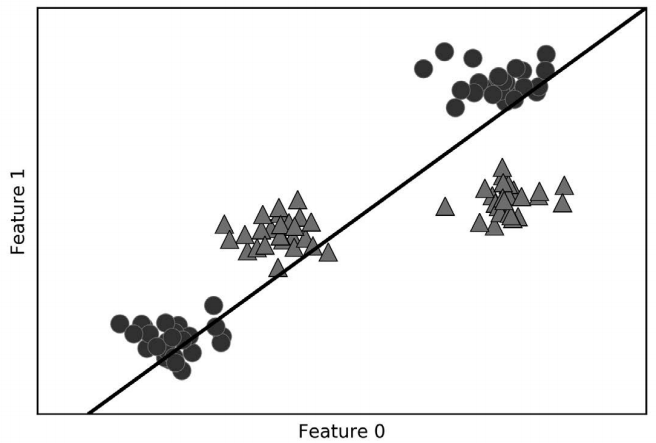

图 2-37：线性 SVM 给出的决策边界

现在我们对输入特征进行扩展，比如说添加第二个特征的平方（feature1 2）作为一个 新特征。现在我们将每个数据点表示为三维点 (feature0, feature1, feature1 2)，而 不是二维点 (feature0, feature1)11。这个新的表示可以画成图 2-38 中的三维散点图：

In[78]:
# 添加第二个特征的平方，作为一个新特征
X_new = np.hstack([X, X[:, 1:] ** 2])
from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
# 3D可视化
ax = Axes3D(figure, elev=-152, azim=-26)
# 首先画出所有y == 0的点，然后画出所有y == 1的点
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
 cmap=mglearn.cm2, s=60)
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
 cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")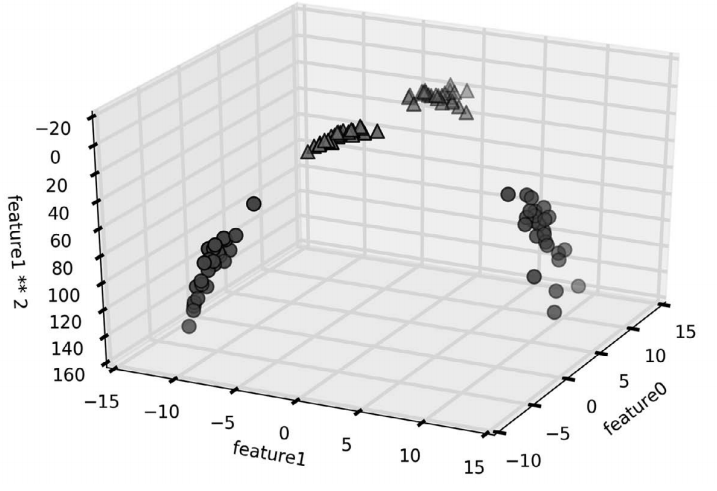

图 2-38：对图 2-37 中的数据集进行扩展，新增由 feature1 导出的的第三个特征

在数据的新表示中，现在可以用线性模型（三维空间中的平面）将这两个类别分开。我们 可以用线性模型拟合扩展后的数据来验证这一点（见图 2-39）：

In[79]:
linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
# 显示线性决策边界
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
 cmap=mglearn.cm2, s=60)
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
 cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1 ** 2")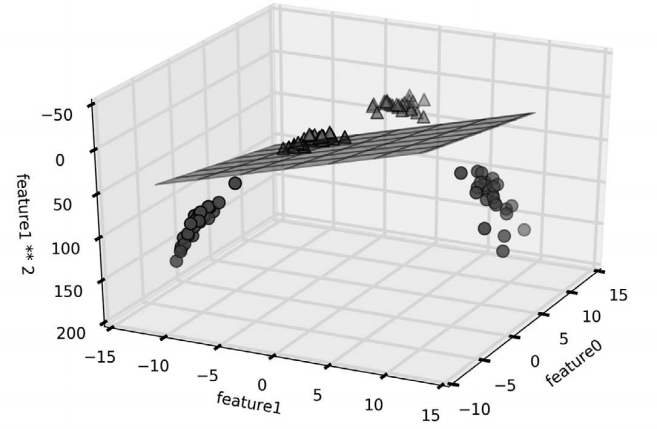

图 2-39：线性 SVM 对扩展后的三维数据集给出的决策边界

如果将线性 SVM 模型看作原始特征的函数，那么它实际上已经不是线性的了。它不是一条直线，而是一个椭圆，你可以在下图中看出（图 2-40）：

In[80]:
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
 cmap=mglearn.cm2, alpha=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")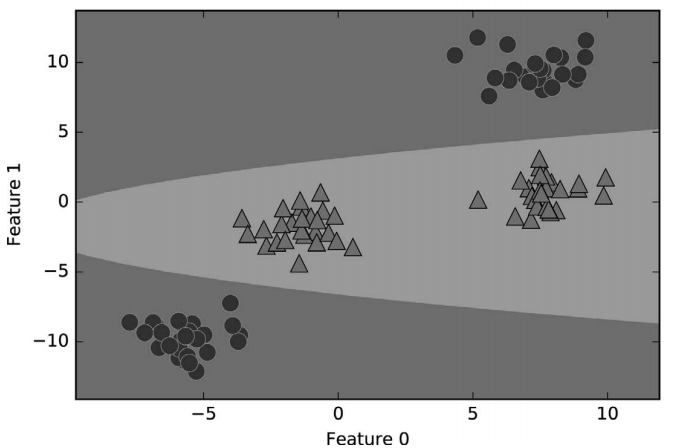

图 2-40：将图 2-39 给出的决策边界作为两个原始特征的函数

2. 核技巧

这里需要记住的是，向数据表示中添加非线性特征，可以让线性模型变得更强大。但是， 通常来说我们并不知道要添加哪些特征，而且添加许多特征（比如 100 维特征空间所有可 能的交互项）的计算开销可能会很大。幸运的是，有一种巧妙的数学技巧，让我们可以在 更高维空间中学习分类器，而不用实际计算可能非常大的新的数据表示。这种技巧叫作核 技巧（kernel trick），它的原理是直接计算扩展特征表示中数据点之间的距离（更准确地说 是内积），而不用实际对扩展进行计算。

对于支持向量机，将数据映射到更高维空间中有两种常用的方法：一种是多项式核，在一 定阶数内计算原始特征所有可能的多项式（比如 feature1 * 2 feature2 ** 5）；另一 种是径向基函数（radial basis function，RBF）核，也叫高斯核。高斯核有点难以解释，因 为它对应无限维的特征空间。一种对高斯核的解释是它考虑所有阶数的所有可能的多项 式，但阶数越高，特征的重要性越小。

不过在实践中，核 SVM 背后的数学细节并不是很重要，可以简单地总结出使用 RBF 核 SVM 进行预测的方法——我们将在下一节介绍这方面的内容。

3. 理解SVM

在训练过程中，SVM 学习每个训练数据点对于表示两个类别之间的决策边界的重要性。通 常只有一部分训练数据点对于定义决策边界来说很重要：位于类别之间边界上的那些点。 这些点叫作支持向量（support vector），支持向量机正是由此得名。

想要对新样本点进行预测，需要测量它与每个支持向量之间的距离。分类决策是基于它与 支持向量之间的距离以及在训练过程中学到的支持向量重要性（保存在 SVC 的 dualcoef 属性中）来做出的。

数据点之间的距离由高斯核给出：

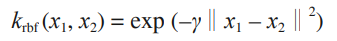
这里 x1 和 x2 是数据点，‖x1 - x2‖ 表示欧氏距离，γ（gamma）是控制高斯核宽度的参数。

图 2-41 是支持向量机对一个二维二分类数据集的训练结果。决策边界用黑色表示，支持向 量是尺寸较大的点。下列代码将在 forge 数据集上训练 SVM 并创建此图：

In[81]:
from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# 画出支持向量
sv = svm.support_vectors_
# 支持向量的类别标签由dual_coef_的正负号给出
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")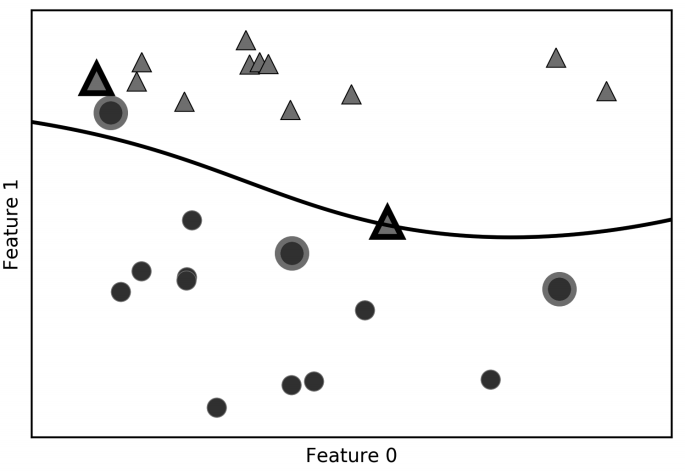

图 2-41：RBF 核 SVM 给出的决策边界和支持向量

在这个例子中，SVM 给出了非常平滑且非线性（不是直线）的边界。这里我们调节了两 个参数：C 参数和 gamma 参数，下面我们将详细讨论。

4. SVM调参

gamma 参数是上一节给出的公式中的参数，用于控制高斯核的宽度。它决定了点与点之间 “靠近”是指多大的距离。C 参数是正则化参数，与线性模型中用到的类似。它限制每个点 的重要性（或者更确切地说，每个点的 dualcoef）。

我们来看一下，改变这些参数时会发生什么（图 2-42）：

In[82]:
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]):
 for a, gamma in zip(ax, range(-1, 2)):
 mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)
axes[0, 0].legend(["class 0", "class 1", "sv class 0", "sv class 1"],
 ncol=4, loc=(.9, 1.2))

图 2-42：设置不同的 C 和 gamma 参数对应的决策边界和支持向量

从左到右，我们将参数 gamma 的值从 0.1 增加到 10。gamma 较小，说明高斯核的半径较大， 许多点都被看作比较靠近。这一点可以在图中看出：左侧的图决策边界非常平滑，越向右 的图决策边界更关注单个点。小的 gamma 值表示决策边界变化很慢，生成的是复杂度较低 的模型，而大的 gamma 值则会生成更为复杂的模型。

从上到下，我们将参数 C 的值从 0.1 增加到 1000。与线性模型相同，C 值很小，说明模型 非常受限，每个数据点的影响范围都有限。你可以看到，左上角的图中，决策边界看起来 几乎是线性的，误分类的点对边界几乎没有任何影响。再看左下角的图，增大 C 之后这些 点对模型的影响变大，使得决策边界发生弯曲来将这些点正确分类。

我们将 RBF 核 SVM 应用到乳腺癌数据集上。默认情况下，C=1，gamma=1/n_features：

In[83]:
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, random_state=0)
svc = SVC()
svc.fit(X_train, y_train)
print("Accuracy on training set: {:.2f}".format(svc.score(X_train, y_train)))
print("Accuracy on test set: {:.2f}".format(svc.score(X_test, y_test)))

Out[83]:
Accuracy on training set: 1.00
Accuracy on test set: 0.63

这个模型在训练集上的分数十分完美，但在测试集上的精度只有 63%，存在相当严重的过 拟合。虽然 SVM 的表现通常都很好，但它对参数的设定和数据的缩放非常敏感。特别地， 它要求所有特征有相似的变化范围。我们来看一下每个特征的最小值和最大值，它们绘制 在对数坐标上（图 2-43）：

In[84]:
plt.plot(X_train.min(axis=0), 'o', label="min")
plt.plot(X_train.max(axis=0), '^', label="max")
plt.legend(loc=4)
plt.xlabel("Feature index")
plt.ylabel("Feature magnitude")
plt.yscale("log")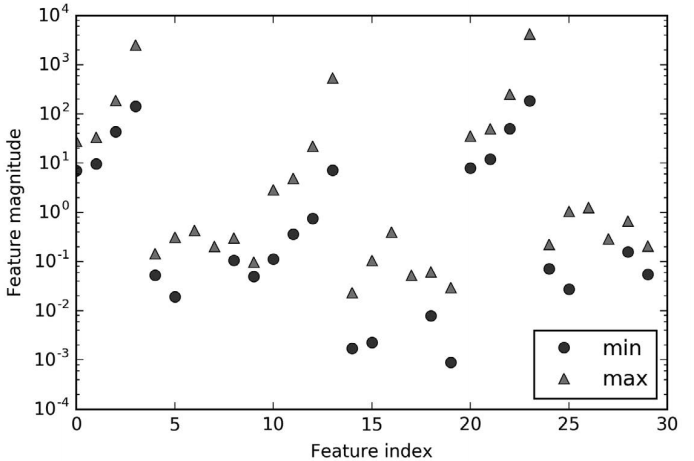

图 2-43：乳腺癌数据集的特征范围（注意 y 轴的对数坐标）

从这张图中，我们可以确定乳腺癌数据集的特征具有完全不同的数量级。这对其他模型来 说（比如线性模型）可能是小问题，但对核 SVM 却有极大影响。我们来研究处理这个问 题的几种方法。

5. 为SVM预处理数据

解决这个问题的一种方法就是对每个特征进行缩放，使其大致都位于同一范围。核 SVM 常用的缩放方法就是将所有特征缩放到 0 和 1 之间。我们将在第 3 章学习如何使用 MinMaxScaler 预处理方法来做到这一点，到时会给出更多细节。现在我们来“人工”做到 这一点：

In[85]:
# 计算训练集中每个特征的最小值
min_on_training = X_train.min(axis=0)
# 计算训练集中每个特征的范围（最大值-最小值）
range_on_training = (X_train - min_on_training).max(axis=0)
# 减去最小值，然后除以范围
# 这样每个特征都是min=0和max=1
X_train_scaled = (X_train - min_on_training) / range_on_training
print("Minimum for each feature\n{}".format(X_train_scaled.min(axis=0)))
print("Maximum for each feature\n {}".format(X_train_scaled.max(axis=0)))

Out[85]:
Minimum for each feature
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Maximum for each feature
 [ 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

In[86]:
# 利用训练集的最小值和范围对测试集做相同的变换（详见第3章）
X_test_scaled = (X_test - min_on_training) / range_on_training

In[87]:
svc = SVC()
svc.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(
 svc.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(svc.score(X_test_scaled, y_test)))

Out[87]:
Accuracy on training set: 0.948
Accuracy on test set: 0.951

数据缩放的作用很大！实际上模型现在处于欠拟合的状态，因为训练集和测试集的性能非 常接近，但还没有接近 100% 的精度。从这里开始，我们可以尝试增大 C 或 gamma 来拟合 更为复杂的模型。例如：

In[88]:
svc = SVC(C=1000)
svc.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(
 svc.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(svc.score(X_test_scaled, y_test)))

Out[88]:
Accuracy on training set: 0.988
Accuracy on test set: 0.972

在这个例子中，增大 C 可以显著改进模型，得到 97.2% 的精度。

6. 优点、缺点和参数

核支持向量机是非常强大的模型，在各种数据集上的表现都很好。SVM 允许决策边界很 复杂，即使数据只有几个特征。它在低维数据和高维数据（即很少特征和很多特征）上的 表现都很好，但对样本个数的缩放表现不好。在有多达 10 000 个样本的数据上运行 SVM 可能表现良好，但如果数据量达到 100 000 甚至更大，在运行时间和内存使用方面可能会 面临挑战。

SVM 的另一个缺点是，预处理数据和调参都需要非常小心。这也是为什么如今很多应用 中用的都是基于树的模型，比如随机森林或梯度提升（需要很少的预处理，甚至不需要预 处理）。此外，SVM 模型很难检查，可能很难理解为什么会这么预测，而且也难以将模型 向非专家进行解释。

不过 SVM 仍然是值得尝试的，特别是所有特征的测量单位相似（比如都是像素密度）而 且范围也差不多时。

核 SVM 的重要参数是正则化参数 C、核的选择以及与核相关的参数。虽然我们主要讲的是 RBF 核，但 scikit-learn 中还有其他选择。RBF 核只有一个参数 gamma，它是高斯核宽度 的倒数。gamma 和 C 控制的都是模型复杂度，较大的值都对应更为复杂的模型。因此，这 两个参数的设定通常是强烈相关的，应该同时调节。

2.3.8　神经网络（深度学习）

一类被称为神经网络的算法最近以“深度学习”的名字再度流行。虽然深度学习在许多机 器学习应用中都有巨大的潜力，但深度学习算法往往经过精确调整，只适用于特定的使 用场景。这里只讨论一些相对简单的方法，即用于分类和回归的多层感知机（multilayer perceptron，MLP），它可以作为研究更复杂的深度学习方法的起点。MLP 也被称为（普 通）前馈神经网络，有时也简称为神经网络。

1. 神经网络模型

MLP 可以被视为广义的线性模型，执行多层处理后得到结论。

还记得线性回归的预测公式为：

ŷ = w[0] * x[0] + w[1] * x[1] + … + w[p] * x[p] + b

简单来说，ŷ 是输入特征 x[0] 到 x[p] 的加权求和，权重为学到的系数 w[0] 到 w[p]。我们可 以将这个公式可视化，如图 2-44 所示。

In[89]:
display(mglearn.plots.plot_logistic_regression_graph())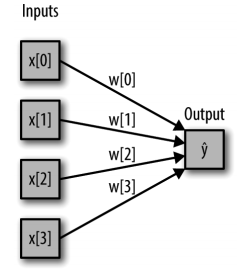

图 2-44：Logistic 回归的可视化，其中输入特征和预测结果显示为结点，系数是结点之间的连线

图中，左边的每个结点代表一个输入特征，连线代表学到的系数，右边的结点代表输出， 是输入的加权求和。

在 MLP 中，多次重复这个计算加权求和的过程，首先计算代表中间过程的隐单元（hidden unit），然后再计算这些隐单元的加权求和并得到最终结果（如图 2-45 所示）：

In[90]:
display(mglearn.plots.plot_single_hidden_layer_graph())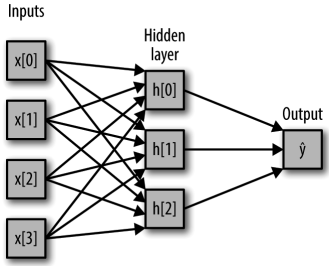

图 2-45：单隐层的多层感知机图示

这个模型需要学习更多的系数（也叫作权重）：在每个输入与每个隐单元（隐单元组成了 隐层）之间有一个系数，在每个隐单元与输出之间也有一个系数。

从数学的角度看，计算一系列加权求和与只计算一个加权求和是完全相同的，因此，为了 让这个模型真正比线性模型更为强大，我们还需要一个技巧。在计算完每个隐单元的加权 求和之后，对结果再应用一个非线性函数——通常是校正非线性（rectifying nonlinearity， 也叫校正线性单元或 relu）或正切双曲线（tangens hyperbolicus，tanh）。然后将这个函数 的结果用于加权求和，计算得到输出 ŷ。这两个函数的可视化效果见图 2-46。relu 截断小于0 的值，而 tanh 在输入值较小时接近 -1，在输入值较大时接近 +1。有了这两种非线性函 数，神经网络可以学习比线性模型复杂得多的函数。

In[91]:
line = np.linspace(-3, 3, 100)
plt.plot(line, np.tanh(line), label="tanh")
plt.plot(line, np.maximum(line, 0), label="relu")
plt.legend(loc="best")
plt.xlabel("x")
plt.ylabel("relu(x), tanh(x)")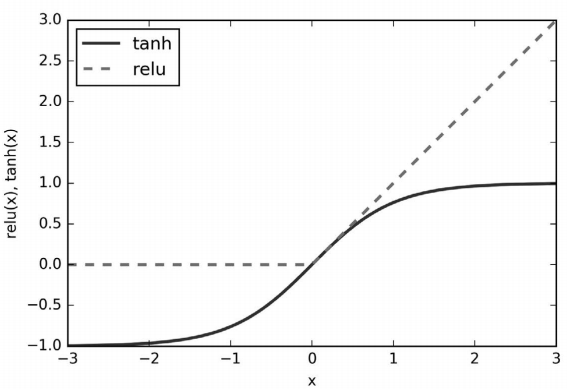

图 2-46：双曲正切激活函数与校正线性激活函数

对于图 2-45 所示的小型神经网络，计算回归问题的 ŷ 的完整公式如下（使用 tanh 非线 性）：

h[0] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * x[2] + w[3, 0] * x[3] + b[0])
h[1] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * x[2] + w[3, 0] * x[3] + b[1])
h[2] = tanh(w[0, 0] * x[0] + w[1, 0] * x[1] + w[2, 0] * x[2] + w[3, 0] * x[3] + b[2])
ŷ = v[0] * h[0] + v[1] * h[1] + v[2] * h[2] + b

其中，w 是输入 x 与隐层 h 之间的权重，v 是隐层 h 与输出 ŷ 之间的权重。权重 w 和 v 要 从数据中学习得到，x 是输入特征，ŷ 是计算得到的输出，h 是计算的中间结果。需要用户 设置的一个重要参数是隐层中的结点个数。对于非常小或非常简单的数据集，这个值可以 小到 10；对于非常复杂的数据，这个值可以大到 10 000。也可以添加多个隐层，如图 2-47 所示。

In[92]:
mglearn.plots.plot_two_hidden_layer_graph()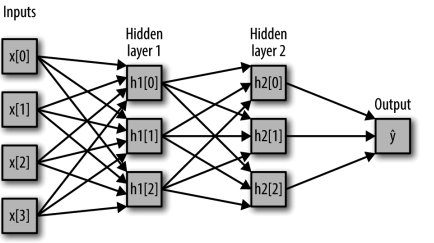

图 2-47：有两个隐层的多层感知机

这些由许多计算层组成的大型神经网络，正是术语“深度学习”的灵感来源。

2. 神经网络调参

我们将 MLPClassifier 应用到本章前面用过的 two_moons 数据集上，以此研究 MLP 的工作 原理。结果如图 2-48 所示。

In[93]:
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
 random_state=42)
mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")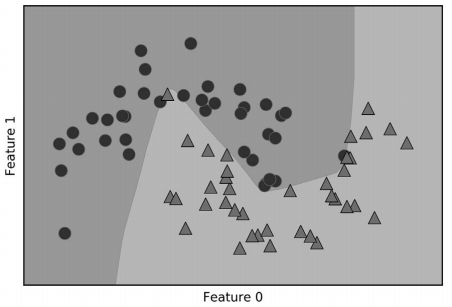

图 2-48：包含 100 个隐单元的神经网络在 two_moons 数据集上学到的决策边界

如你所见，神经网络学到的决策边界完全是非线性的，但相对平滑。我们用到了 solver='lbfgs'，这一点稍后会讲到。

默认情况下，MLP 使用 100 个隐结点，这对于这个小型数据集来说已经相当多了。我们可 以减少其数量（从而降低了模型复杂度），但仍然得到很好的结果（图 2-49）：

In[94]:
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")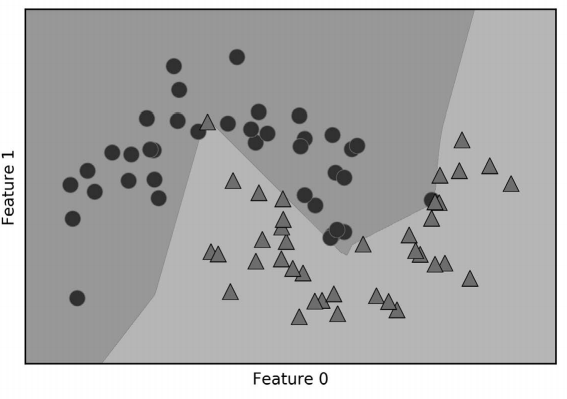

图 2-49：包含 10 个隐单元的神经网络在 two_moons 数据集上学到的决策边界

只有 10 个隐单元时，决策边界看起来更加参差不齐。默认的非线性是 relu，如图 2-46 所 示。如果使用单隐层，那么决策函数将由 10 个直线段组成。如果想得到更加平滑的决策 边界，可以添加更多的隐单元（见图 2-48）、添加第二个隐层（见图 2-50）或者使用 tanh 非线性（见图 2-51）。

In[95]:
# 使用2个隐层，每个包含10个单元
mlp = MLPClassifier(solver='lbfgs', random_state=0,
 hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

In[96]:
# 使用2个隐层，每个包含10个单元，这次使用tanh非线性
mlp = MLPClassifier(solver='lbfgs', activation='tanh',
 random_state=0, hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")

图 2-50：包含 2 个隐层、每个隐层包含 10 个隐单元的神经网络学到的决策边界（激活函数为 relu）

图 2-51：包含 2 个隐层、每个隐层包含 10 个隐单元的神经网络学到的决策边界（激活函数为 tanh）

最后，我们还可以利用 L2 惩罚使权重趋向于 0，从而控制神经网络的复杂度，正如我们在 岭回归和线性分类器中所做的那样。MLPClassifier 中调节 L2 惩罚的参数是 alpha（与线 性回归模型中的相同），它的默认值很小（弱正则化）。图 2-52 显示了不同 alpha 值对 two_ moons 数据集的影响，用的是 2 个隐层的神经网络，每层包含 10 个或 100 个单元：

In[97]:
fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for axx, n_hidden_nodes in zip(axes, [10, 100]):
 for ax, alpha in zip(axx, [0.0001, 0.01, 0.1, 1]):
 mlp = MLPClassifier(solver='lbfgs', random_state=0,
 hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes],
 alpha=alpha)
 mlp.fit(X_train, y_train)
 mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)
 mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)
 ax.set_title("n_hidden=[{}, {}]\nalpha={:.4f}".format(
 n_hidden_nodes, n_hidden_nodes, alpha))

图 2-52：不同隐单元个数与 alpha 参数的不同设定下的决策函数

现在你可能已经认识到了，控制神经网络复杂度的方法有很多种：隐层的个数、每个隐层 中的单元个数与正则化（alpha）。实际上还有更多，但这里不再过多介绍。

神经网络的一个重要性质是，在开始学习之前其权重是随机设置的，这种随机初始化会影 响学到的模型。也就是说，即使使用完全相同的参数，如果随机种子不同的话，我们也可 能得到非常不一样的模型。如果网络很大，并且复杂度选择合理的话，那么这应该不会对 精度有太大影响，但应该记住这一点（特别是对于较小的网络）。图 2-53 显示了几个模型 的图像，所有模型都使用相同的参数设置进行学习：

In[98]:
fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for i, ax in enumerate(axes.ravel()):
 mlp = MLPClassifier(solver='lbfgs', random_state=i,
 hidden_layer_sizes=[100, 100])
 mlp.fit(X_train, y_train)
 mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)
 mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, ax=ax)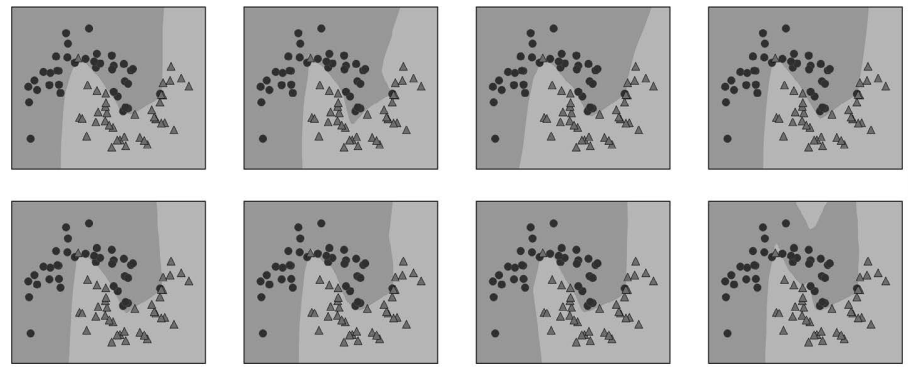

图 2-53：相同参数但不同随机初始化的情况下学到的决策函数

为了在现实世界的数据上进一步理解神经网络，我们将 MLPClassifier 应用在乳腺癌数据 集上。首先使用默认参数：

In[99]:
print("Cancer data per-feature maxima:\n{}".format(cancer.data.max(axis=0)))

Out[99]:
Cancer data per-feature maxima:
[ 28.110 39.280 188.500 2501.000 0.163 0.345 0.427
 0.201 0.304 0.097 2.873 4.885 21.980 542.200
 0.031 0.135 0.396 0.053 0.079 0.030 36.040
 49.540 251.200 4254.000 0.223 1.058 1.252 0.291
 0.664 0.207]

In[100]:
X_train, X_test, y_train, y_test = train_test_split(
 cancer.data, cancer.target, random_state=0)
mlp = MLPClassifier(random_state=42)
mlp.fit(X_train, y_train)
print("Accuracy on training set: {:.2f}".format(mlp.score(X_train, y_train)))
print("Accuracy on test set: {:.2f}".format(mlp.score(X_test, y_test)))

Out[100]:
Accuracy on training set: 0.92
Accuracy on test set: 0.90

MLP 的精度相当好，但没有其他模型好。与较早的 SVC 例子相同，原因可能在于数据的 缩放。神经网络也要求所有输入特征的变化范围相似，最理想的情况是均值为 0、方差为 1。我们必须对数据进行缩放以满足这些要求。同样，我们这里将人工完成，但在第 3 章 将会介绍用 StandardScaler 自动完成：

In[101]:
# 计算训练集中每个特征的平均值
mean_on_train = X_train.mean(axis=0)
# 计算训练集中每个特征的标准差
std_on_train = X_train.std(axis=0)
# 减去平均值，然后乘以标准差的倒数
# 如此运算之后，mean=0，std=1
X_train_scaled = (X_train - mean_on_train) / std_on_train
# 对测试集做相同的变换（使用训练集的平均值和标准差）
X_test_scaled = (X_test - mean_on_train) / std_on_train
mlp = MLPClassifier(random_state=0)
mlp.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(
 mlp.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(mlp.score(X_test_scaled, y_test)))

Out[101]:
Accuracy on training set: 0.991
Accuracy on test set: 0.965
ConvergenceWarning:
 Stochastic Optimizer: Maximum iterations reached and the optimization
 hasn't converged yet.

缩放之后的结果要好得多，而且也相当有竞争力。不过模型给出了一个警告，告诉我们 已经达到最大迭代次数。这是用于学习模型的 adam 算法的一部分，告诉我们应该增加迭 代次数：

In[102]:
mlp = MLPClassifier(max_iter=1000, random_state=0)
mlp.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(
 mlp.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(mlp.score(X_test_scaled, y_test)))

Out[102]:
Accuracy on training set: 0.995
Accuracy on test set: 0.965

增加迭代次数仅提高了训练集性能，但没有提高泛化性能。不过模型的表现相当不错。由 于训练性能和测试性能之间仍有一些差距，所以我们可以尝试降低模型复杂度来得到更好 的泛化性能。这里我们选择增大 alpha 参数（变化范围相当大，从 0.0001 到 1），以此向 权重添加更强的正则化：

In[103]:
mlp = MLPClassifier(max_iter=1000, alpha=1, random_state=0)
mlp.fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(
 mlp.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}".format(mlp.score(X_test_scaled, y_test)))

Out[103]:
Accuracy on training set: 0.988
Accuracy on test set: 0.972

这得到了与我们目前最好的模型相同的性能。

虽然可以分析神经网络学到了什么，但这通常比分析线性模型或基于树的模型更为复杂。 要想观察模型学到了什么，一种方法是查看模型的权重。你可以在 scikit-learn 示例库中 查看这样的一个示例（http://scikit-learn.org/stable/auto_examples/neural_networks/plot_mnist_filters.html）。对于乳腺癌数据集，这可能有点难以理解。下面这张图（图 2-54）显示了连 接输入和第一个隐层之间的权重。图中的行对应 30 个输入特征，列对应 100 个隐单元。 浅色代表较大的正值，而深色代表负值。

In[104]:
plt.figure(figsize=(20, 5))
plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis')
plt.yticks(range(30), cancer.feature_names)
plt.xlabel("Columns in weight matrix")
plt.ylabel("Input feature")
plt.colorbar()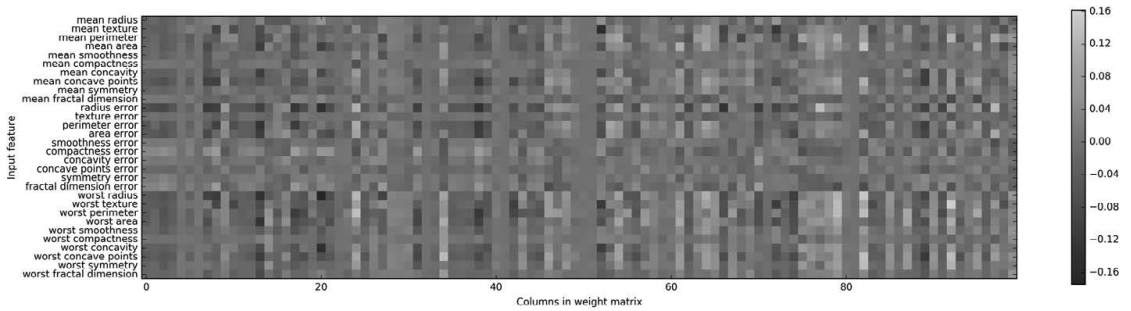

图 2-54：神经网络在乳腺癌数据集上学到的第一个隐层权重的热图

我们可以推断，如果某个特征对所有隐单元的权重都很小，那么这个特征对模型来说就 “不太重要”。可以看到，与其他特征相比，“mean smoothness”“mean compactness”以及 “smoothness error”和“fractal dimension error”之间的特征的权重都相对较小。这可能说 明这些特征不太重要，也可能是我们没有用神经网络可以使用的方式来表示这些特征。

我们还可以将连接隐层和输出层的权重可视化，但它们更加难以解释。

虽然 MLPClassifier 和 MLPRegressor 为最常见的神经网络架构提供了易于使用的接口，但 它们只包含神经网络潜在应用的一部分。如果你有兴趣使用更灵活或更大的模型，我们建议你看一下除了 scikit-learn 之外的很棒的深度学习库。对于 Python 用户来说，最为完 善的是 keras、lasagna 和 tensor-flow。lasagna 是基于 theano 库构建的，而 keras 既可 以用 tensor-flow 也可以用 theano。这些库提供了更为灵活的接口，可以用来构建神经网 络并跟踪深度学习研究的快速发展。所有流行的深度学习库也都允许使用高性能的图形处 理单元（GPU），而 scikit-learn 不支持 GPU。使用 GPU 可以将计算速度加快 10 到 100 倍，GPU 对于将深度学习方法应用到大型数据集上至关重要。

3. 优点、缺点和参数

在机器学习的许多应用中，神经网络再次成为最先进的模型。它的主要优点之一是能够获 取大量数据中包含的信息，并构建无比复杂的模型。给定足够的计算时间和数据，并且仔 细调节参数，神经网络通常可以打败其他机器学习算法（无论是分类任务还是回归任务）。

这就引出了下面要说的缺点。神经网络——特别是功能强大的大型神经网络——通常需要 很长的训练时间。它还需要仔细地预处理数据，正如我们这里所看到的。与 SVM 类似， 神经网络在“均匀”数据上的性能最好，其中“均匀”是指所有特征都具有相似的含义。 如果数据包含不同种类的特征，那么基于树的模型可能表现得更好。神经网络调参本身也 是一门艺术。调节神经网络模型和训练模型的方法有很多种，我们只是蜻蜓点水地尝试了 几种而已。

估计神经网络的复杂度。最重要的参数是层数和每层的隐单元个数。你应该首先设置 1 个 或 2 个隐层，然后可以逐步增加。每个隐层的结点个数通常与输入特征个数接近，但在几 千个结点时很少会多于特征个数。

在考虑神经网络的模型复杂度时，一个有用的度量是学到的权重（或系数）的个数。如果 你有一个包含 100 个特征的二分类数据集，模型有 100 个隐单元，那么输入层和第一个隐 层之间就有 100 100 = 10 000 个权重。在隐层和输出层之间还有 100 1 = 100 个权重，总 共约 10 100 个权重。如果添加含有 100 个隐单元的第二个隐层，那么在第一个隐层和第二 个隐层之间又有 100 100 = 10 000 个权重，总数变为约 20 100 个权重。如果你使用包含 1000 个隐单元的单隐层，那么在输入层和隐层之间需要学习 100 1000 = 100 000 个权重， 隐层到输出层之间需要学习 1000 1 = 1000 个权重，总共 101 000 个权重。如果再添加第 二个隐层，就会增加 1000 1000 = 1 000 000 个权重，总数变为巨大的 1 101 000 个权重， 这比含有 2 个隐层、每层 100 个单元的模型要大 50 倍。

神经网络调参的常用方法是，首先创建一个大到足以过拟合的网络，确保这个网络可以对 任务进行学习。知道训练数据可以被学习之后，要么缩小网络，要么增大 alpha 来增强正 则化，这可以提高泛化性能。

在我们的实验中，主要关注模型的定义：层数、每层的结点个数、正则化和非线性。这些 内容定义了我们想要学习的模型。还有一个问题是，如何学习模型或用来学习参数的算 法，这一点由 solver 参数设定。solver 有两个好用的选项。默认选项是 'adam'，在大多 数情况下效果都很好，但对数据的缩放相当敏感（因此，始终将数据缩放为均值为 0、方 差为 1 是很重要的）。另一个选项是 'lbfgs'，其鲁棒性相当好，但在大型模型或大型数据 集上的时间会比较长。还有更高级的 'sgd' 选项，许多深度学习研究人员都会用到。'sgd' 选项还有许多其他参数需要调节，以便获得最佳结果。你可以在用户指南中找到所有这些参数及其定义。当你开始使用 MLP 时，我们建议使用 'adam' 和 'lbfgs'。

fit 会重置模型

scikit-learn 模型的一个重要性质就是，调用 fit 总会重置模型之前学到的 所有内容。因此，如果你在一个数据集上构建模型，然后在另一个数据集上再次 调用 fit，那么模型会“忘记”从第一个数据集中学到的所有内容。你可以 对一个模型多次调用 fit，其结果与在“新”模型上调用 fit 是完全相同的。

2.4　分类器的不确定度估计

我们还没有谈到 scikit-learn 接口的另一个有用之处，就是分类器能够给出预测的不确 定度估计。一般来说，你感兴趣的不仅是分类器会预测一个测试点属于哪个类别，还包括 它对这个预测的置信程度。在实践中，不同类型的错误会在现实应用中导致非常不同的结 果。想象一个用于测试癌症的医疗应用。假阳性预测可能只会让患者接受额外的测试，但 假阴性预测却可能导致重病没有得到治疗。第 6 章会进一步探讨这一主题。

scikit-learn 中有两个函数可用于获取分类器的不确定度估计：decision_function 和 predict_proba。大多数分类器（但不是全部）都至少有其中一个函数，很多分类器两个都 有。我们来构建一个 GradientBoostingClassifier 分类器（同时拥有 decision_function 和 predict_proba 两个方法），看一下这两个函数对一个模拟的二维数据集的作用：

In[105]:
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_circles
X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
# 为了便于说明，我们将两个类别重命名为"blue"和"red"
y_named = np.array(["blue", "red"])[y]
# 我们可以对任意个数组调用train_test_split
# 所有数组的划分方式都是一致的
X_train, X_test, y_train_named, y_test_named, y_train, y_test = \
 train_test_split(X, y_named, y, random_state=0)
# 构建梯度提升模型
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train_named)

2.4.1　决策函数

对于二分类的情况，decision_function 返回值的形状是 (n_samples,)，为每个样本都返回 一个浮点数：

In[106]:
print("X_test.shape: {}".format(X_test.shape))
print("Decision function shape: {}".format(
 gbrt.decision_function(X_test).shape))

Out[106]:
X_test.shape: (25, 2)
Decision function shape: (25,)

对于类别 1 来说，这个值表示模型对该数据点属于“正”类的置信程度。正值表示对正类 的偏好，负值表示对“反类”（其他类）的偏好：

In[107]:
# 显示decision_function的前几个元素
print("Decision function:\n{}".format(gbrt.decision_function(X_test)[:6]))

Out[107]:
Decision function:
[ 4.136 -1.683 -3.951 -3.626 4.29 3.662]

我们可以通过仅查看决策函数的正负号来再现预测值：

In[108]:
print("Thresholded decision function:\n{}".format(
 gbrt.decision_function(X_test) > 0))
print("Predictions:\n{}".format(gbrt.predict(X_test)))

Out[108]:
Thresholded decision function:
[ True False False False True True False True True True False True
 True False True False False False True True True True True False
 False]
Predictions:
['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
 'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
 'red' 'blue' 'blue']

对于二分类问题，“反”类始终是 classes 属性的第一个元素，“正”类是 classes 的第 二个元素。因此，如果你想要完全再现 predict 的输出，需要利用 classes_ 属性：

In[109]:
# 将布尔值True/False转换成0和1
greater_zero = (gbrt.decision_function(X_test) > 0).astype(int)
# 利用0和1作为classes_的索引
pred = gbrt.classes_[greater_zero]
# pred与gbrt.predict的输出完全相同
print("pred is equal to predictions: {}".format(
 np.all(pred == gbrt.predict(X_test))))

Out[109]:
pred is equal to predictions: True

decision_function 可以在任意范围取值，这取决于数据与模型参数：

In[110]:
decision_function = gbrt.decision_function(X_test)
print("Decision function minimum: {:.2f} maximum: {:.2f}".format(
 np.min(decision_function), np.max(decision_function)))

Out[110]:
Decision function minimum: -7.69 maximum: 4.29

由于可以任意缩放，因此 decision_function 的输出往往很难解释。

在下面的例子中，我们利用颜色编码在二维平面中画出所有点的 decision_function，还有 决策边界，后者我们之间见过。我们将训练点画成圆，将测试数据画成三角（图 2-55）：

In[111]:
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0], alpha=.4,
 fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1],
 alpha=.4, cm=mglearn.ReBl)
for ax in axes:
 # 画出训练点和测试点
 mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1], y_test,
 markers='^', ax=ax)
 mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train,
 markers='o', ax=ax)
 ax.set_xlabel("Feature 0")
 ax.set_ylabel("Feature 1")
cbar = plt.colorbar(scores_image, ax=axes.tolist())
axes[0].legend(["Test class 0", "Test class 1", "Train class 0",
 "Train class 1"], ncol=4, loc=(.1, 1.1))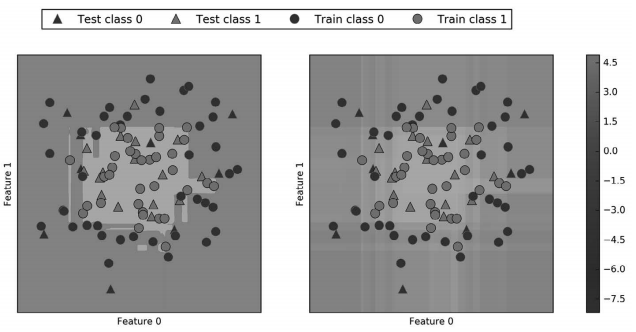

图 2-55：梯度提升模型在一个二维玩具数据集上的决策边界（左）和决策函数（右）

既给出预测结果，又给出分类器的置信程度，这样给出的信息量更大。但在上面的图像 中，很难分辨出两个类别之间的边界。

2.4.2　预测概率

predict_proba 的输出是每个类别的概率，通常比 decision_function 的输出更容易理解。 对于二分类问题，它的形状始终是 (n_samples, 2)：

In[112]:
print("Shape of probabilities: {}".format(gbrt.predict_proba(X_test).shape))

Out[112]:
Shape of probabilities: (25, 2)

每行的第一个元素是第一个类别的估计概率，第二个元素是第二个类别的估计概率。由于 predict_proba 的输出是一个概率，因此总是在 0 和 1 之间，两个类别的元素之和始终为 1：

In[113]:
# 显示predict_proba的前几个元素
print("Predicted probabilities:\n{}".format(
 gbrt.predict_proba(X_test[:6])))

Out[113]:
Predicted probabilities:
[[ 0.016 0.984]
 [ 0.843 0.157]
 [ 0.981 0.019]
 [ 0.974 0.026]
 [ 0.014 0.986]
 [ 0.025 0.975]]

由于两个类别的概率之和为 1，因此只有一个类别的概率超过 50%。这个类别就是模型的 预测结果。1

在上一个输出中可以看到，分类器对大部分点的置信程度都是相对较高的。不确定度大小 实际上反映了数据依赖于模型和参数的不确定度。过拟合更强的模型可能会做出置信程度 更高的预测，即使可能是错的。复杂度越低的模型通常对预测的不确定度越大。如果模型 给出的不确定度符合实际情况，那么这个模型被称为校正（calibrated）模型。在校正模型 中，如果预测有 70% 的确定度，那么它在 70% 的情况下正确。

在下面的例子中（图 2-56），我们再次给出该数据集的决策边界，以及类别 1 的类别概率：

In[114]:
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
mglearn.tools.plot_2d_separator(
 gbrt, X, ax=axes[0], alpha=.4, fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(
 gbrt, X, ax=axes[1], alpha=.5, cm=mglearn.ReBl, function='predict_proba')
for ax in axes:
 # 画出训练点和测试点
  mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1], y_test,
 markers='^', ax=ax)
 mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train,
 markers='o', ax=ax)
 ax.set_xlabel("Feature 0")
 ax.set_ylabel("Feature 1")
cbar = plt.colorbar(scores_image, ax=axes.tolist())
axes[0].legend(["Test class 0", "Test class 1", "Train class 0",
 "Train class 1"], ncol=4, loc=(.1, 1.1))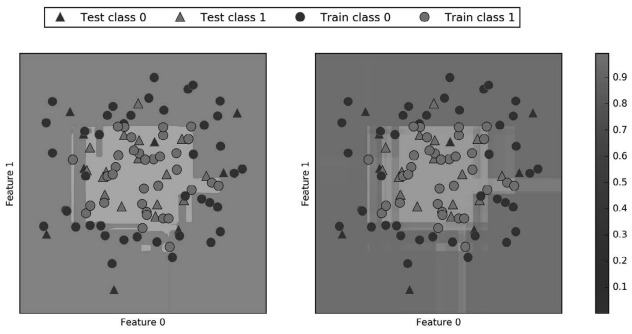

图 2-56：图 2-55 中梯度提升模型的决策边界（左）和预测概率

这张图中的边界更加明确，不确定的小块区域清晰可见。

scikit-learn 网 站（http://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html）给出了许多模型的对比，以及不确定度估计的形状。我们在图 2-57 中 复制了这一结果，我们也建议你去网站查看那些示例。

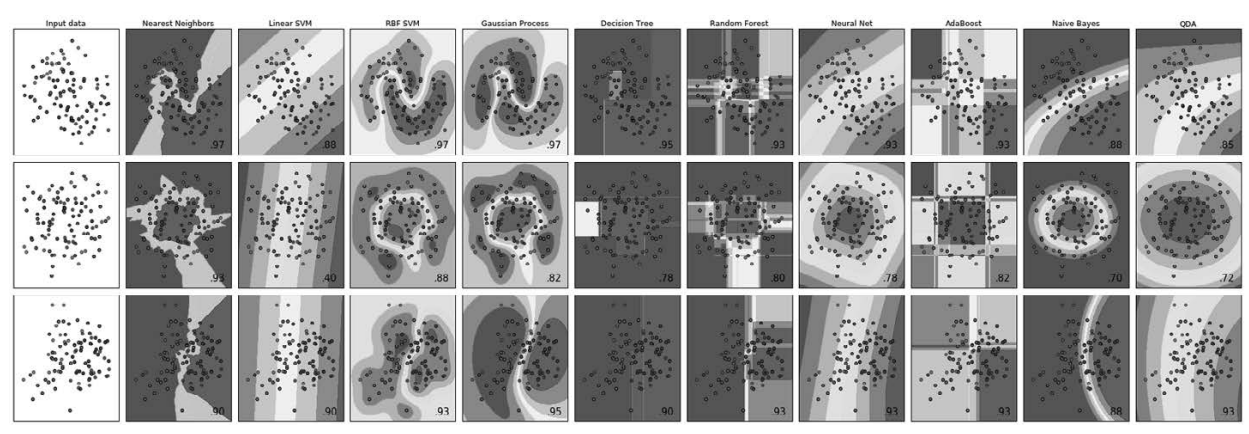
图 2-57：scikit-learn 中几种分类器在模拟数据集上的对比（图片来源：http://scikit-learn.org）

2.4.3　多分类问题的不确定度

到目前为止，我们只讨论了二分类问题中的不确定度估计。但 decision_function 和 predict_proba 也适用于多分类问题。我们将这两个函数应用于鸢尾花（Iris）数据集，这 是一个三分类数据集：

In[115]:
from sklearn.datasets import load_iris
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(
 iris.data, iris.target, random_state=42)
gbrt = GradientBoostingClassifier(learning_rate=0.01, random_state=0)
gbrt.fit(X_train, y_train)

In[116]:
print("Decision function shape: {}".format(gbrt.decision_function(X_test).shape))
# 显示决策函数的前几个元素
print("Decision function:\n{}".format(gbrt.decision_function(X_test)[:6, :]))

Out[116]:
Decision function shape: (38, 3)
Decision function:
[[-0.529 1.466 -0.504]
 [ 1.512 -0.496 -0.503]
 [-0.524 -0.468 1.52 ]
 [-0.529 1.466 -0.504]
 [-0.531 1.282 0.215]
 [ 1.512 -0.496 -0.503]]

对于多分类的情况，decision_function 的形状为 (n_samples, n_classes)，每一列对应每 个类别的“确定度分数”，分数较高的类别可能性更大，得分较低的类别可能性较小。你 可以找出每个数据点的最大元素，从而利用这些分数再现预测结果：

In[117]:
print("Argmax of decision function:\n{}".format(
 np.argmax(gbrt.decision_function(X_test), axis=1)))
print("Predictions:\n{}".format(gbrt.predict(X_test)))

Out[117]:
Argmax of decision function:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1 0]
Predictions:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1 0]

predict_proba 输出的形状相同，也是 (n_samples, n_classes)。同样，每个数据点所有可 能类别的概率之和为 1：

In[118]:
# 显示predict_proba的前几个元素
print("Predicted probabilities:\n{}".format(gbrt.predict_proba(X_test)[:6]))
# 显示每行的和都是1
print("Sums: {}".format(gbrt.predict_proba(X_test)[:6].sum(axis=1)))

Out[118]:
Predicted probabilities:
[[ 0.107 0.784 0.109]
 [ 0.789 0.106 0.105]
 [ 0.102 0.108 0.789]
 [ 0.107 0.784 0.109]
 [ 0.108 0.663 0.228]
 [ 0.789 0.106 0.105]]
Sums: [ 1. 1. 1. 1. 1. 1.]

同样，我们可以通过计算 predict_proba 的 argmax 来再现预测结果：

In[119]:
print("Argmax of predicted probabilities:\n{}".format(
 np.argmax(gbrt.predict_proba(X_test), axis=1)))
print("Predictions:\n{}".format(gbrt.predict(X_test)))

Out[119]:
Argmax of predicted probabilities:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1 0]
Predictions:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1 0]

总 之，predict_proba 和 decision_function 的 形 状 始 终 相 同， 都 是 (nsamples, n classes)——除了二分类特殊情况下的 decisionfunction。对于二分类的情况，decision function 只有一列，对应“正”类 classes_[1]。这主要是由于历史原因。

如果有 n_classes 列，你可以通过计算每一列的 argmax 来再现预测结果。但如果类别 是字符串，或者是整数，但不是从 0 开始的连续整数的话，一定要小心。如果你想要对 比 predict 的结果与 decision_function 或 predictproba 的结果，一定要用分类器的 classes 属性来获取真实的属性名称：

In[120]:
logreg = LogisticRegression()
# 用Iris数据集的类别名称来表示每一个目标值
named_target = iris.target_names[y_train]
logreg.fit(X_train, named_target)
print("unique classes in training data: {}".format(logreg.classes_))
print("predictions: {}".format(logreg.predict(X_test)[:10]))
argmax_dec_func = np.argmax(logreg.decision_function(X_test), axis=1)
print("argmax of decision function: {}".format(argmax_dec_func[:10]))
print("argmax combined with classes_: {}".format(
 logreg.classes_[argmax_dec_func][:10]))

Out[120]:
unique classes in training data: ['setosa' 'versicolor' 'virginica']
predictions: ['versicolor' 'setosa' 'virginica' 'versicolor' 'versicolor'
 'setosa' 'versicolor' 'virginica' 'versicolor' 'versicolor']
 argmax of decision function: [1 0 2 1 1 0 1 2 1 1]
argmax combined with classes_: ['versicolor' 'setosa' 'virginica' 'versicolor'
 'versicolor' 'setosa' 'versicolor' 'virginica' 'versicolor' 'versicolor']

2.5　小结与展望

本章首先讨论了模型复杂度，然后讨论了泛化，或者说学习一个能够在前所未见的新数据上表现良好的模型。这就引出了欠拟合和过拟合的概念，前者是指一个模型无法获取训练数据中的所有变化，后者是指模型过分关注训练数据，但对新数据的泛化性能不好。

然后本章讨论了一系列用于分类和回归的机器学习模型，各个模型的优点和缺点，以及如何控制它们的模型复杂度。我们发现，对于许多算法而言，设置正确的参数对模型性能至 关重要。有些算法还对输入数据的表示方式很敏感，特别是特征的缩放。因此，如果盲目地将一个算法应用于数据集，而不去理解模型所做的假设以及参数设定的含义，不太可能会得到精度高的模型。

本章包含大量有关算法的信息，在继续阅读后续章节之前你不必记住所有这些细节。但是，这里提到的有关模型的某些知识（以及在特定情况下使用哪种模型）对于在实践中成功应用机器学习模型是很重要的。关于何时使用哪种模型，下面是一份快速总结。

最近邻

适用于小型数据集，是很好的基准模型，很容易解释。

线性模型

非常可靠的首选算法，适用于非常大的数据集，也适用于高维数据。

朴素贝叶斯

只适用于分类问题。比线性模型速度还快，适用于非常大的数据集和高维数据。精度通常要低于线性模型。

决策树

速度很快，不需要数据缩放，可以可视化，很容易解释。

随机森林

几乎总是比单棵决策树的表现要好，鲁棒性很好，非常强大。不需要数据缩放。不适用于高维稀疏数据。

梯度提升决策树

精度通常比随机森林略高。与随机森林相比，训练速度更慢，但预测速度更快，需要的内存也更少。比随机森林需要更多的参数调节。

支持向量机

对于特征含义相似的中等大小的数据集很强大。需要数据缩放，对参数敏感。

神经网络

可以构建非常复杂的模型，特别是对于大型数据集而言。对数据缩放敏感，对参数选取 敏感。大型网络需要很长的训练时间。

面对新数据集，通常最好先从简单模型开始，比如线性模型、朴素贝叶斯或最近邻分类 器，看能得到什么样的结果。对数据有了进一步了解之后，你可以考虑用于构建更复杂模 型的算法，比如随机森林、梯度提升决策树、SVM 或神经网络。

现在你应该对如何应用、调节和分析我们介绍过的模型有了一定的了解。本章主要介绍了 二分类问题，因为这通常是最容易理解的。不过本章大多数算法都可以同时用于分类和回归，而且所有分类算法都可以同时用于二分类和多分类。你可以尝试将这些算法应用于 scikit-learn 的内置数据集，比如用于回归的 boston_housing 或 diabetes 数据集，或者用 于多分类的 digits 数据集。在不同的数据集上实验这些算法，可以让你更好地感受它们所需的训练时间、分析模型的难易程度以及它们对数据表示的敏感程度。

虽然我们分析了不同的参数设定对算法的影响，但在生产环境中实际构建一个对新数据泛 化性能很好的模型要更复杂一些。我们将在第 6 章介绍正确调参的方法和自动寻找最佳参 数的方法。

不过首先，我们将在下一章深入讨论无监督学习和预处理。

转载请注明：xuhss » Python机器学习基础篇二《监督学习》