Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475
本文为手稿，旨在搞清楚为什么BPTT算法会多路反向求导，而不是一个感性的认识。

假设我们要对E3求导（上图中的L3），那么则有：

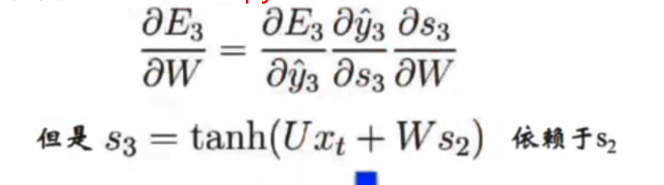
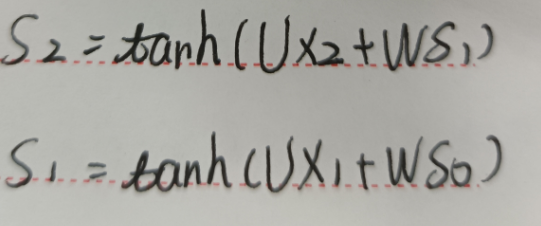
所以S2是W的函数，也就是说，我们不能说：

因为WS2 = WS2(w)，S2里面包含了W这个变量，S2是W的函数，也许有人会说：“S2里面的W是常数吧”，那么请想一想S2的一般表达式。（这里我其实还是有点过不去，但是我觉得应该是这样的，不知道各位是否有理解方法）

所以有：

而对函数WS2(w)求导（对W求导），结果为：

S02和W2在RNN中的位置为：

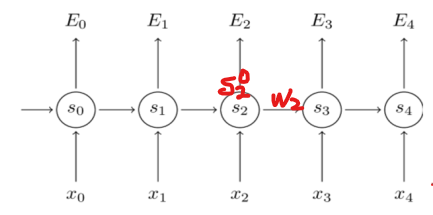
再次注意，上面两个值不是变量，是一个具体的值。

然后再求(WS1)`:

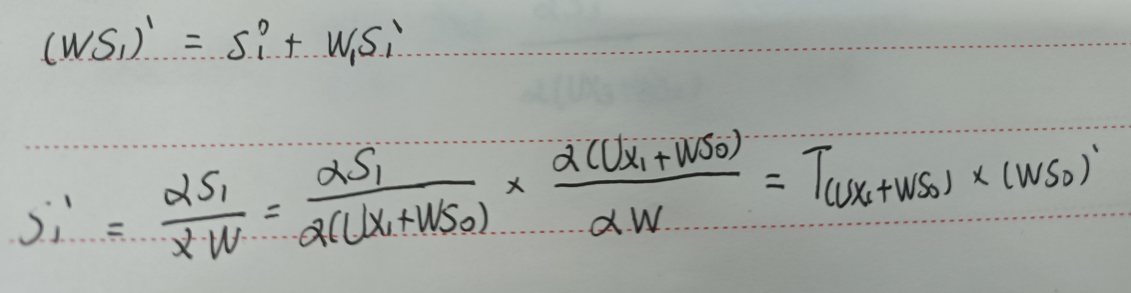
另外关于W1，这里我不太清楚是否继续要用W2，因为毕竟是对第t=3时刻的W求导，如果后面知道了，再改也不迟。

继续求下去：

我们假设S-1是全0的向量，那么S0`就会是0.

然后，我们把上面分开求的结果合并起来，直接计算S3对W的导数：

最后一行就是最终的结果，其实这三项分别对应：

下面是数学表示：

所以，

BPTT反向求导为什么必然会有多路，实际上是因为 S2是W的函数，所以要运用乘法求导法则，最后完全求出(S2W)`之后，便可以写成这样的形式：

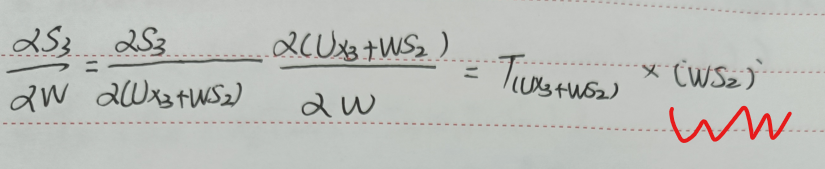
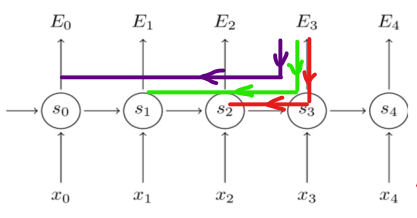
以下是完整草稿：

本文截图部分来自我的NLP课程乔波老师的PPT。

转载请注明：xuhss » 从乘法求导法则到BPTT算法