? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
今天学了前缀和和差分,为了避免我把它忘掉,我还是浅浅的记录一下吧
首先需要知道什么是前缀和与差分:

前缀和就是数组中某元素之前(包括此元素)的所有元素的和
设b[]为前缀和数组,a[]是原数组。
对于一维数组而言,某个元素的前缀和就是从这个数组的第0个元素到这个元素的所有元素之和。
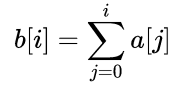
即:
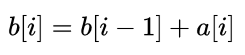
那么就可以对区间求和产生更深刻的理解:
对于求出一个区间[l,r]的所有元素之和,我们就可以将首元素的前缀和与末元素的前缀合相减。
代码如下:
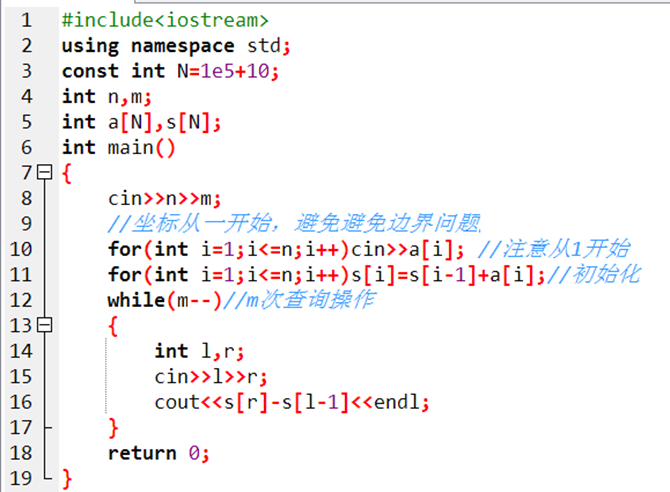
而对于二维数组来说,每个元素的前缀和b[x][y]就是从a[0][0]到a[x][y]之间所有元素的和
比如b[3][1],就可以如下图的方法表示:

而如果我想给一个区间求和,就直接表示为:
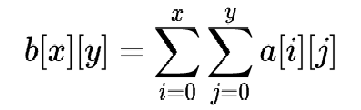
即: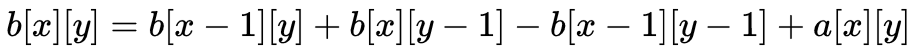
那我要是想给一个区间求和,就可以表示为:
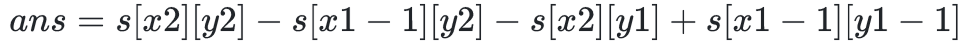

代码如下:
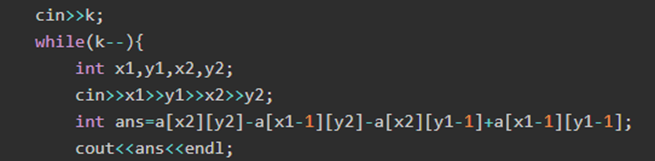
关于差分,就是将当前元素与前一个元素相减。
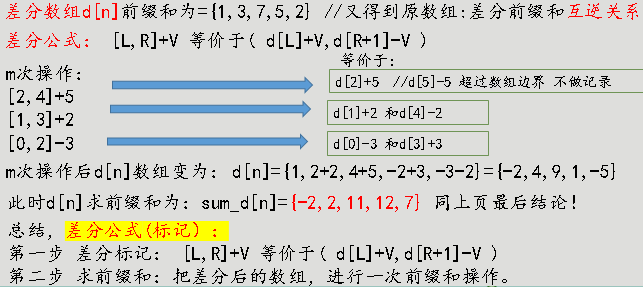
比如给定一个数组a[n]={1,3,7,5,2},他的差分数组就是d[n]={1,2,4,-2,-3}
他的应用有很多,比如:给定一个序列,m次访问,每次输入两个一维坐x1,x2,并输入一个数c,代表这个数列从第x1个数到第x2个数之间的元素都加c,最后输出最新的序列。
对于这种题,先求出这个序列的差分数组d,每次询问让[L,R]+V转化为d[L]+V,d[R+1]-V ,最后再将新数组求一次前缀和即可。
对于二维差分
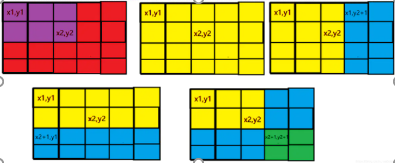
现在我要在左上角是 (x1,y1),右下角是 (x2,y2) 的矩形区间每个值都 +p
那如果开始位置+p,那根据前缀和的性质,那么它影响的就是整个黄色部分(所有的求和都增加了),多影响了两个蓝色部分。所以在两个蓝色部分 -p 消除 +p 的影响,而两个蓝色部分重叠的绿色部分多了个 -p 的影响,所以绿色部分 +p 消除影响
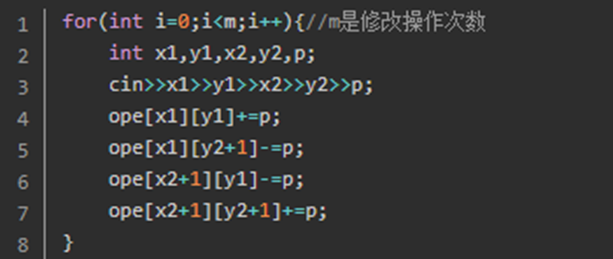
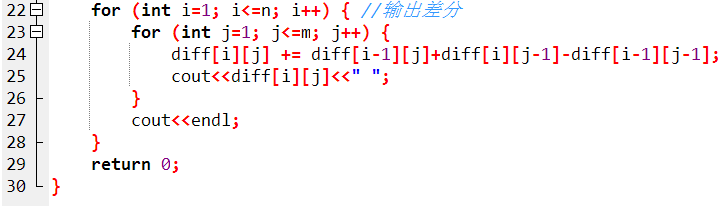
代码如下:

关于lowbit()函数
lowbit(x)是x的二进制表达式中最低位的1所对应的值
比如12的二进制可以表示为1100,所以他的lowbit就是1*8等于8
关于他的代码实现也很简单
1 int lowbit(int x)
2 {
3 return x&(-x);
4 //实际上就是负数的补码运用
5 }如何用lowbit()来维护其区间
设结点的编号为x,那么这个结点维护的区间就是 (x-lowbit(x),x](注意区间的开闭)
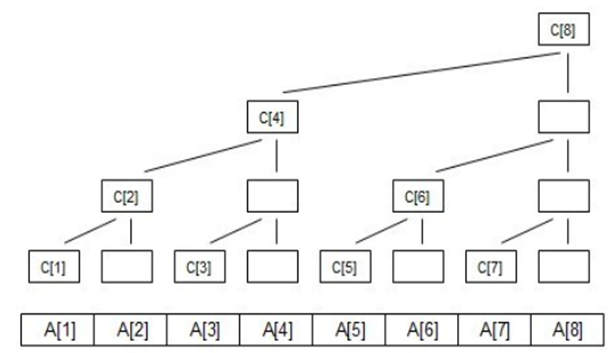
c1维护区间(1-lowbit(1),1]即(0,1] 也就是A1本身
c2维护区间(2-lowbit(2),2]即(0,2] A1+A2
c3维护(2,3] A3
c4维护(0,4] A1+A2+A3+A4
c5维护(4,5] A5
c6维护(4,6] A5+A6
c7维护(6,7] A7
c8维护(0,8] A1+A2+A3+A4+A5+A6+A7+A8
不难发现,结点维护的叶结点(A单点区间)的个数就是其序号转换为二进制后lowbit的值
通过寻找规律,可以得到通式:
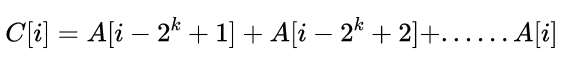
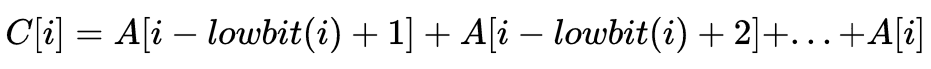
寻找树状数组的性质:
(性质1)每个内部结点C[x]保存以它为根的子树中所有叶结点的和。
(性质2)每个内部结点C[x]的子结点个数等于lowbit(x)的值。
(性质3)除树根以外,每个内部结点C[x]的父亲结点是C[x+lowbit(x)]
(性质4)树的深度为O(logN)
通过这些性质,我们可以进行一系列操作:
1、查询前缀和:
1 int lowbit(x)
2 {
3 return x&(-x);
4 }
5
6 int sum(int x)//查询前缀和(c[x]的区间和)
7 {
8 int res=0;
9 while(x>0)
10 {
11 res=res+c[x];
12 x=x-lowbit(x);
13 }
14 return res;
15 }2.单点修改:
1 int lowbit(int x)
2 {
3 return x&(-x);
4 }
5 void update(int x,int y)
6 //a[x]+y操作,并让他的长辈加y
7 {
8 while(x<=n)
9 {
10 c[x]+=y;
11 x+=lowbit(x);
12 }
13 }3、区间和计算
int calculate(int x,int y)
{
return sum(y)-sum(x-1);
}经典题目:
1 #include
2 #include
3 using namespace std;
4 int c[100001];
5 int n,m,k,a,b;
6 int lowbit(int x)
7 {
8 return x&(-x);
9 }
10
11 void update(int x,int v)
12 //单点修改(在x的位置上加v)
13 {
14 while(x<=n)
15 {
16 c[x]+=v;
17 x+=lowbit(x);
18 }
19 }
20
21 int sum(int x)
22 {
23 int res=0;
24 while(x>0)
25 {
26 res+=c[x];
27 x-=lowbit(x);
28 }
29 return res;
30 }
31
32 int main()
33 {
34 int v;
35 scanf("%d%d",&n,&m);
36 for(int i=1;i<=n;i++)
37 {
38 scanf("%d",&v);
39 update(i,v);
40 }
41 for(int i=1;i<=m;i++)
42 {
43 scanf("%d%d%d",&k,&a,&b);
44 if(k==0) printf("%d\n",sum(b)-sum(a-1));
45 else update(a,b);
46 }
47 return 0;
48 }就先到这里吧,再见!
转载请注明:xuhss » 关于区间操作查找(前缀和与差分)+树状数组基础