? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
毕设中用到了很多代码,其中一部分我通过看书和看论文学习并实现的代码,会通过Gitee仓库分享出来,这些代码仅用于学习使用,祝各位毕业生顺利完成毕设!
毕设系列内容:毕业设计——四自由度机械臂轨迹规划
毕设(5)—笛卡尔空间轨迹规划(直线、圆弧)
机械臂在笛卡尔空间中常用的规划算法有直线和圆弧两种,他们的具体实现都是通过运动学逆解将运动轨迹转化为关节角度变化序列的方式。
直线轨迹规划
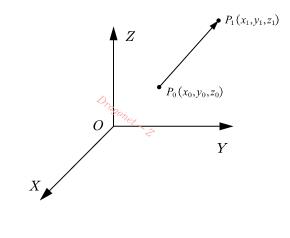
设机械臂任务是从空间中两点P1P1P_1、P2P2P_2间运动,如下图所示
则两点长度LLL可得
L=(x1−x0)2+(y1−y0)2+(z1−z0)2−−−−−−−−−−−−−−−−−−−−−−−−−−−√L=(x1−x0)2+(y1−y0)2+(z1−z0)2L=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2+(z_1-z_0)^2}
在本文中采用的速度规划是匀速,如果有S型之类的速度规划算法也可以采用
d=v⋅td=v⋅td=v\cdot t
d为一个插补周期内移动的距离,t为插补的时间间隔
圆弧轨迹规划
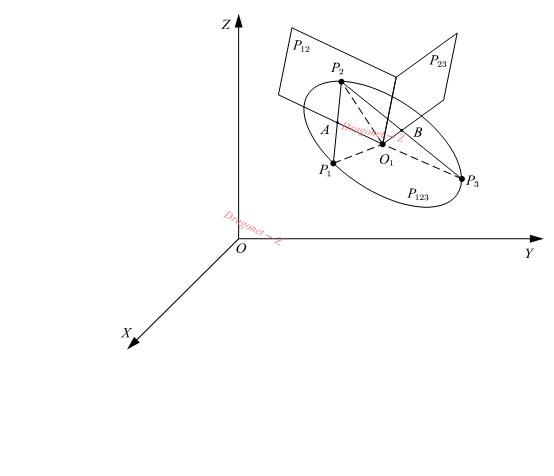
空间中两两不在同一条直线的三点可确定一个平面,也可以确定一个圆弧。设空间中有三点P1P1P_1、P2P2P_2、P3P3P_3,机械臂需要通过三点沿圆弧轨迹运动,如下图所示
矢量图我用的是AxGlyph软件画的,有需要可以自行到官网购买
公式太多,不再赘述,大致流程如下
- 求出P123P123P_{123}、P12P12P_{12}和P23P23P_{23}的方程,通过三个平面方程获得圆心O1O1O_1坐标和圆弧半径
- 在P123P123P_{123}平面建立新坐标系,计算两个坐标系之间的齐次变换矩阵
- 在P123P123P_{123}平面计算平面圆弧的轨迹,通过变换矩阵转换为空间圆弧轨迹
- 圆弧轨迹通过运动学逆解转换为各关节角度变化序列
Matlab代码验证
代码有点长,具体函数代码可以到仓库中自行查找
test4.m
clear, clc, close all;
L(1) = Link([0 0 0 0 0 0], 'modified');
L(2) = Link([0 0 0 -pi / 2 0 0], 'modified');
L(3) = Link([0 0 135 0 0 0], 'modified');
L(4) = Link([0 0 147 0 0 0], 'modified');
L(5) = Link([0 131 61 -pi / 2 0 0], 'modified');
robot = SerialLink(L, 'name', 'Dobot');
angle1 = [-pi / 3, -pi / 9, pi / 3, -2 * pi / 9, 0];
angle2 = [-pi / 9, -pi / 3, pi / 2, -pi / 6, pi / 9];
angle3 = [7 * pi / 36, -pi / 4, 5 * pi / 12, -pi / 6, 2 * pi / 9];
angle4 = [4 * pi / 9, -pi / 9, 7 * pi / 18, -5 * pi / 18, pi / 3];
angleT = [angle1; angle2; angle3];
for i = 1:size(angleT, 1)
fk = myfkine(angleT(i, :));
points(i, :) = [fk(1, 4), fk(2, 4), fk(3, 4)];
theta5(i) = angleT(i, 5);
end
[q, t] = line_traj(points, theta5, [0, 5], 100);
%[q, t] = arc\_traj(points, theta5, [0, 5, 10], 40);
qdeg = rad2deg(q);
figure(1);
T = zeros(4, 4, size(q, 1));
for i = 1:size(q, 1)
T(:, :, i) = myfkine(q(i, :));
end
plot3(squeeze(T(1, 4, :)), squeeze(T(2, 4, :)), squeeze(T(3, 4, :)), 'r-', 'LineWidth', 2);
title('轨迹图');
hold on;
plot3(points(:, 1), points(:, 2), points(:, 3), 'bo', 'MarkerSize', 7, 'LineWidth', 2);
hold on;
robot.plot(q);
grid on;
hold on;
figure(2);
plot(t, qdeg);
title('角度图');
legend('q\_1', 'q\_2', 'q\_3', 'q\_4', 'q\_5');
xlabel('t(s)');
ylabel('deg(°)');
grid on;
hold on;
直线规划运行结果如下
| 直线轨迹图 | 直线角度图 |
圆弧规划运行结果如下
| 圆弧轨迹图 | 圆弧角度图 |
可以注意到圆弧角度图在t=5秒时刻有一次跳变,应该是我重新写函数的时候漏了一些东西没写(pointT向量长度是2step+1,而q向量长度为2step,我重写函数的时候直接去掉中间的一位pointT了)
for i = 0:theta13 / (2 * step - 1):theta13 %这个地方我直接减1了,原来我写的函数是没有这个的
pointT(j, :) = transT * [R * cos(i), R * sin(i), 0, 1]';
j = j + 1;
end
本文到此结束,后续会继续更新的~?
转载请注明:xuhss » 毕设(5)—笛卡尔空间轨迹规划(直线、圆弧)