Python微信订餐小程序课程视频

https://edu.csdn.net/course/detail/36074

Python实战量化交易理财系统

https://edu.csdn.net/course/detail/35475

定义

在一幅无向图 G=(V,E)G=(V,E)G=(V,E) 中，(u,v)(u,v)(u, v) 为连接顶点 uuu 和顶点 vvv 的边，w(u,v)w(u,v)w(u,v) 为边的权重，若存在边的子集 T⊆ET⊆ET\subseteq E 且 (V,T)(V,T)(V,T) 为树，使得

w(T)=∑(u,v)∈Tw(u,v)w(T)=∑(u,v)∈Tw(u,v)w(T)=\sum_{(u,v)\in T}w(u,v)
最小，这称 TTT 为图 GGG 的最小生成树。

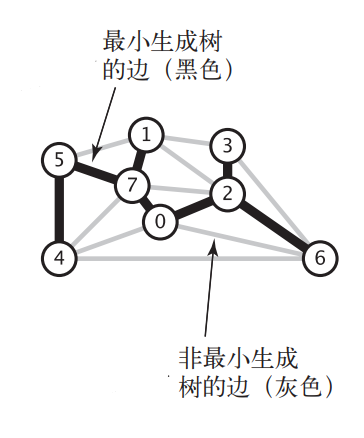
说的通俗点，最小生成树就是带权无向图中权值和最小的树。下图中黑色边所标识的就是一棵最小生成树（图片来自《算法第四版》），对于权值各不相同的连通图来说最小生成树只会有一棵：

带权图的实现

在 《如何在 Java 中实现无向图》 中我们使用邻接表数组实现了无向图，其中邻接表上的每个节点的数据域只是一个整数，代表着一个顶点。为了方便最小生成树的迭代，我们将数据域换成 Edge 实例。Edge 有三个成员：顶点 v、顶点 w 和权重 weight，为了比较每一条边的权重，需要实现 Comparable 接口。代码如下所示：

复制package com.zhiyiyo.graph;

/**
 * 图中的边
 */
public class Edge implements Comparable {
 private final int v, w;
 private final double weight;

 public Edge(int v, int w, double weight) {
 this.v = v;
 this.w = w;
 this.weight = weight;
 }

 /**
 * 返回边中的一个顶点
 */
 int either() {
 return v;
 }

 /**
 * 返回边中的拎一个顶点
 *
 * @param v 顶点 v
 * @return 另一个顶点
 */
 int another(int v) {
 if (this.v == v) {
 return w;
 } else if (w == v) {
 return this.v;
 } else {
 throw new RuntimeException("边中不存在该顶点");
 }
 }

 public double getWeight() {
 return weight;
 }

 @Override
 public String toString() {
 return String.format("Edge{%d-%d %f}", v, w, weight);
 }

 @Override
 public int compareTo(Edge edge) {
 return Double.compare(weight, edge.weight);
 }
}

之后只要照猫画虎，将 LinkGraph 的泛型从 Integer 换成 Edge 就行了：

复制package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;

/**
 * 带权无向图
 */
public class WeightedGraph {
    private final int V;
    protected int E;
    protected LinkStack[] adj;

 public WeightedGraph(int V) {
 this.V = V;
 adj = (LinkStack[]) new LinkStack[V];
 for (int i = 0; i < V; i++) {
 adj[i] = new LinkStack<>();
 }
 }

 public int V() {
 return V;
 }

 public int E() {
 return E;
 }

 public void addEdge(Edge edge) {
 int v = edge.either();
 int w = edge.another(v);
 adj[v].push(edge);
 adj[w].push(edge);
 E++;
 }

 public Iterable adj(int v) {
 return adj[v];
 }

 /**
 * 获取所有边
 */
 public Iterable edges() {
 Stack edges = new LinkStack<>();
 for (int v = 0; v < V; ++v) {
 for (Edge edge : adj(v)) {
 if (edge.another(v) > v) {
 edges.push(edge);
 }
 }
 }

 return edges;
 }
}

同时给出最小生成树的 API：

复制package com.zhiyiyo.graph;

/**
 * 最小生成树
 */
public interface MST {
    /**
 * 获取最小生成树中的所有边
 */
    Iterable edges();

 /**
 * 获取最小生成树的权重
 */
 double weight();
}

Kruskal 算法

假设 EEE 是图 GGG 中所有边的集合，TTT 是最小生成树的边集合，kruskal 算法的思想是每次从 EEE 中弹出权值最小的边 ememe_m，如果 ememe_m 不会和 TTT 中的边构成环，就将其加入 TTT 中，直到 |T|=|V|−1|T|=|V|−1|T|=|V|-1 也就是 TTT 中边的个数是图 GGG 的顶点个数 -1 时，就得到了最小生成树。

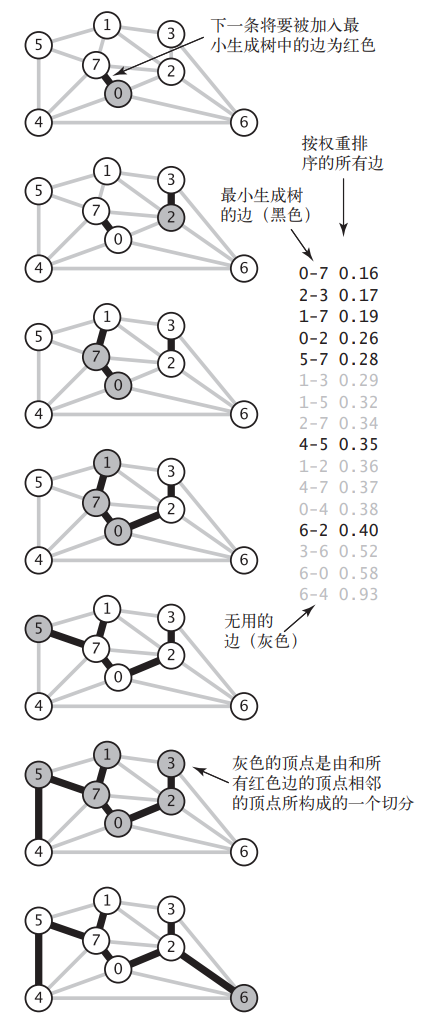
对于上一幅图，使用 kruskal 算法得到最小生成树的过程如下图所示：

首先将 EEE 中最小的边 0-7 弹出并加到 TTT 中，此时的 EEE 中最小边为 2-3，虽然 2-3 和 0-7 无法构成连通图，但是没关系，只要贪心地将其加入 TTT 中即可，因为后续其他边的添加总会将二者连通起来。接着按照权值的升序依次把边 1-7、0-2、5-7 加到 TTT 中，直到碰到边 1-3，如果把 1-3 加入 TTT 中，就会出现环 1-3-2-0-7-1，所以直接将 1-3 舍弃，1-5、2-7 也同理被丢弃掉。由于边 4-5 不会在 TTT 中构成环，所以将其加入 TTT。重复上述步骤，直到 |T|=|V|−1|T|=|V|−1|T|=|V|-1。

上述过程中有两个影响性能的地方，一个是找出 EEE 中权值最小的边 ememe_m，一个是判断将 ememe_m 加到 TTT 中是否会出现环。

二叉堆

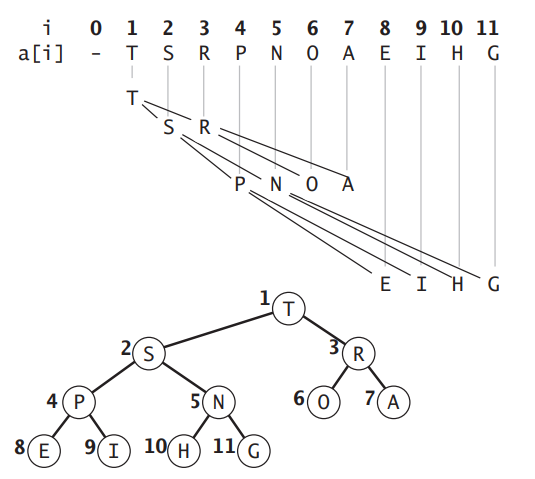
二叉堆是一棵完全二叉树，且每个父节点总是大于等于（最大堆）或者小于等于（最小堆）他的子节点。《算法第四版》中给出了使用数组存储的最大堆的结构，其中数组下标为 0 的地方不存储元素，假设下标为 iii 出存放的是父节点，那么 2i2i2i 和 2i+12i+12i+1 处就是子节点：

由于最小堆的堆顶节点总是最小的，所以只需将 EEE 变为一个最小堆，每次取出堆顶的元素即可，时间复杂度为 O(logN)O(log⁡N)O(\log N)。下面来看下如何实现最小堆。

API

对于一个二叉堆，我们关心以下操作：

复制package com.zhiyiyo.collection.queue;

public interface PriorQueueextends Comparable> {
 /**
 * 向堆中插入一个元素
 * @param item 插入的元素
 */
 void insert(T item);

 /**
 * 弹出堆顶的元素
 * @return 堆顶元素
 */
 T pop();

 /**
 * 获取堆中的元素个数
 */
 int size();

 /**
 * 堆是否为空
 */
 boolean isEmpty();
}

插入

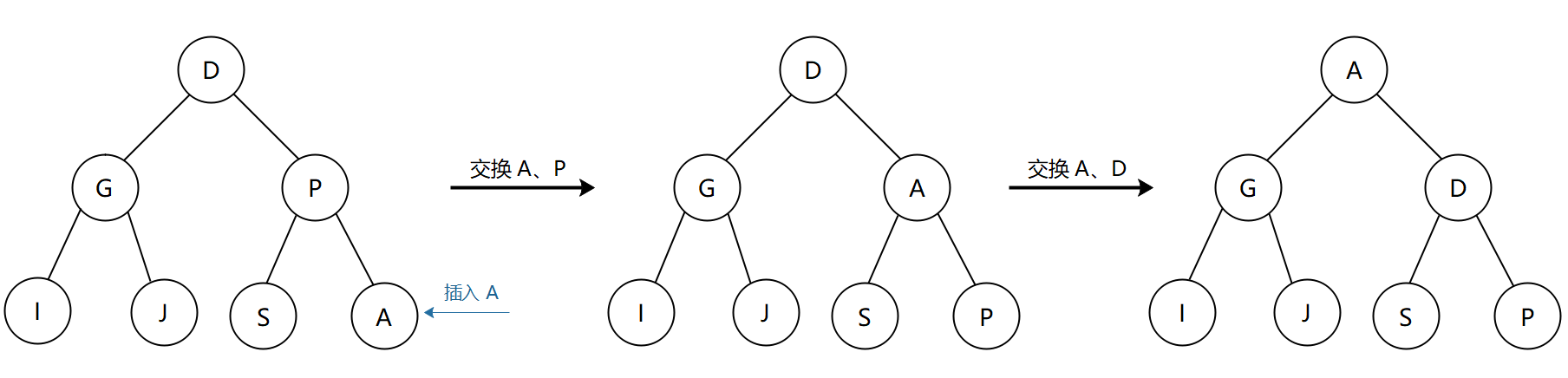
为了保证二叉堆是一棵完全二叉树，每次都将新节点插到数组的末尾，也就是二叉树的最后一个节点。如下图所示，假设插入的节点为 A，它的父节点为 P，兄弟节点为 S，由于 P > A，这就打破了二叉堆的有序性，所以需要对堆进行调整。具体流程就是将兄弟节点中的较小者（A）选为父节点，而先前的父节点 P 则退位变为子节点。如果此时 A 的父节点小于 A，则无需继续调整。但是下图中只交换了 A、P 之后还是没将二叉树调整为堆有序状态，因为父节点 D > A，接着将兄弟节点中较小的 A 变为父节点，而 D 则变成 A 的子节点，至此完成最小堆的调整。

上述过程的代码如下所示，为了保证后续插入操作，每当数组满员时就对其进行扩容操作：

复制package com.zhiyiyo.collection.queue;

import java.util.Arrays;

public class MinPriorQueueextends Comparable> implements PriorQueue{
 private T[] array;
 private int N;

 public MinPriorQueue() {
 this(3);
 }

 public MinPriorQueue(int maxSize) {
 array = (T[]) new Comparable[maxSize + 1];
 }

 @Override
 public boolean isEmpty() {
 return N == 0;
 }

 @Override
 public int size() {
 return N;
 }

 @Override
 public void insert(T item) {
 array[++N] = item;
 swim(N);
 if (N == array.length - 1) resize(1 + 2 * N);
 }

 /**
 * 元素上浮
 *
 * @param k 元素的索引
 */
 private void swim(int k) {
 while (k > 1 && less(k, k / 2)) {
 swap(k, k / 2);
 k /= 2;
 }
 }

 private void swap(int a, int b) {
 T tmp = array[a];
 array[a] = array[b];
 array[b] = tmp;
 }

 private boolean less(int a, int b) {
 return array[a].compareTo(array[b]) < 0;
 }

 private void resize(int size) {
 array = Arrays.copyOf(array, size);
 }
}

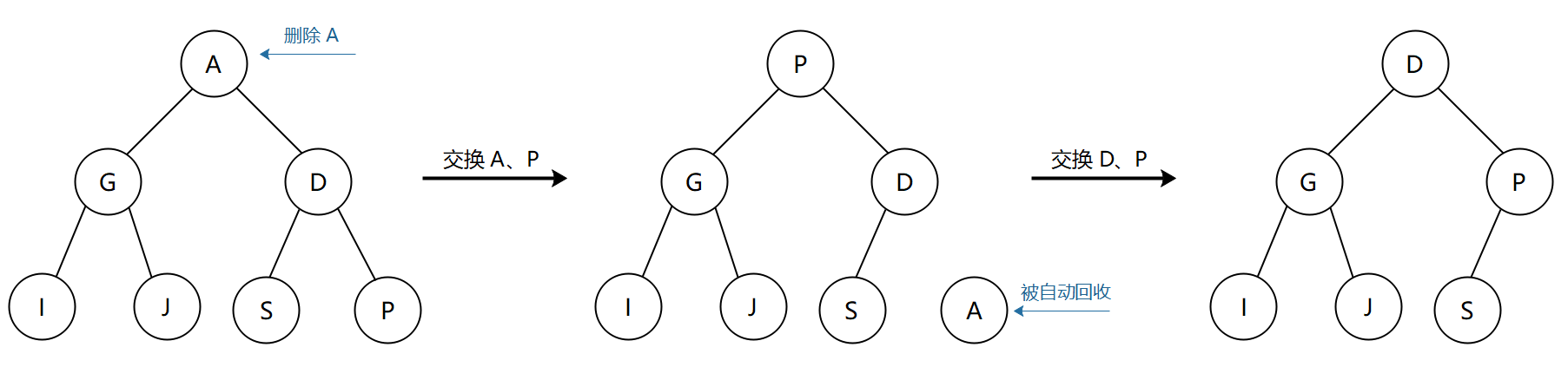
删除最小元素

假设我们需要删除下图中的 A 元素，这时候就需要将 A 和最小堆的最后一个元素 P 交换位置，并将数组的最后一个元素置为 null，使得 A 的引用次数变为 0，能被垃圾回收机制自动回收掉。交换之后最小堆的有序性被破坏了，因为父节点 P > 子节点 D，这时候和插入元素的操作一样，将较小的子节点和父节点交换位置，使得较大的父节点能够下沉，而较小的子节点上位，这个过程持续到没有子节点被 P 更小为止。

实现代码如下：

复制@Override
public T pop() {
    T item = array[1];
    swap(1, N);
    array[N--] = null;
    sink(1);
    if (N < (array.length - 1) / 4) resize((array.length - 1) / 2);
    return item;
}

/**
 * 元素下沉
 *
 * @param k 元素的索引
 */
private void sink(int k) {
    while (2 * k <= N) {
        int j = 2 * k;
        // 检查是否有两个子节点
        if (j < N && less(j + 1, j)) j++;
        if (less(k, j)) break;
        swap(k, j);
        k = j;
    }
}

并查集

假设 TTT 中的顶点的集合为 V′V′V'，则有图 G′=(V′,T)G′=(V′,T)G'=(V', T)。我们可以将 G′G′G' 划分为 nnn 个连通分量，每个连通分量有一个标识 id∈[0,n−1]id∈[0,n−1]id\in [0, n-1]。要想判断将边 ememe_m 加入 TTT 后是否会构成环，只需判断 ememe_m 的两个顶点是都属于同一个连通分量即可。

判断是否连通

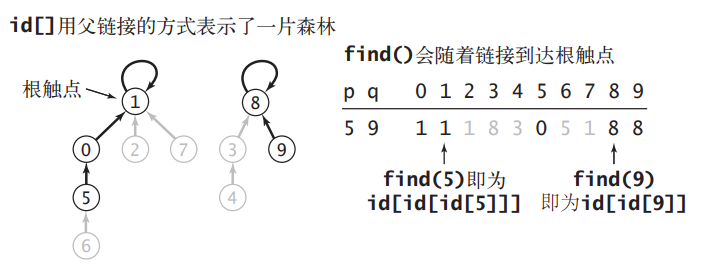
由于每个连通分量都不存在环，可以看作一棵小树，所以可以用一个数组 int[] ids 的索引表示树中的节点（图中的顶点），而索引处的元素值为父节点的索引值，数组中 ids[i] == i 的位置就是每棵树的根节点，i 就是这个连通分量的标识。而我们想要知道两个节点之间是否连通，只需判断他们所属的树的根节点是否相同即可。

假设从树底的叶节点 6 出发，一路向上直到树顶 1，中间需要经过 5 和 0 两个节点，如果节点 6 的根节点查询得比较频繁，那么这种查找效率是比较低的。由于我们只需知道根节点是谁即可，树的结构无关紧要，那么为何不想个办法把节点 5、6 直接挂到根节点 1，这样只要一步就能知道根节点。实现这种想法的的方式就是路径压缩：当从节点 6 走到父节点 5 时，就将节点 6 挂到节点 5 的父节点 0 上；而从节点 0 走到根节点 1 时，就将子节点 6 和 5 挂到根节点 1 下，树高被压缩为 1。

实现上述过程的代码如下所示：

复制package com.zhiyiyo.collection.tree;

public class UnionFind {
    private int[] ids;
    private int[] ranks;    // 每棵树的高度
    private int N;          // 树的数量

    public UnionFind(int N) {
        this.N = N;
        ids = new int[N];
        ranks = new int[N];
        for (int i = 0; i < N; i++) {
            ids[i] = i;
            ranks[i] = 1;
        }
    }

    /**
 * 获取连通分量个数
 *
 * @return 连通分量个数
 */
    public int count() {
        return N;
    }

    /**
 * 获得连通分量的 id
 *
 * @param p 触点 id
 * @return 连通分量 id
 */
    public int find(int p) {
        while (p != ids[p]) {
            ids[p] = ids[ids[p]];   // 路径压缩
            p = ids[p];
        }
        return p;
    }

    /**
 * 判断两个触点是否连通
 *
 * @param p 触点 p 的 id
 * @param q 触点 q 的 id
 * @return 是否连通
 */
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }
}

合并连通分量

我们将 EEE 中的 ememe_m 添加到 TTT 中时，ememe_m 的两个节点肯定分属于两个连通分量，加入 TTT 之后就需要将这两个分量合并，也就是将两棵小树合并为一颗大树。假设两棵树的高度分别为 h1h1h_1 和 h2h2h_2，如果直接将一颗树的根节点接到另一棵树的叶节点上，会导致新树高度为 h1+h2h1+h2h_1+h_2，降低寻找根节点的效率。解决方式是按秩归并，将矮树的根节点接到高树的根节点上，会出现两种情况：

• 如果 h1≠h2h1≠h2h_1 \neq h_2，新树高度会是 max{h1,h2}max{h1,h2}\max{h_1, h_2}
• 如果 h1=h2=ch1=h2=ch_1=h_2=c，新树高度会是 c+1c+1c+1

上述过程的代码如下所示：

复制/**
 * 如果两个触点不处于同一个连通分量中，则连接两个触点
 *
 * @param p 触点 p 的 id
 * @param q 触点 q 的 id
 */
public void union(int p, int q) {
    int pId = find(p);
    int qId = find(q);
    if (qId == pId) return;

    // 将小树并到大树
    if (ranks[qId] > ranks[pId]) {
        ids[pId] = qId;
    } else if (ranks[qId] < ranks[pId]) {
        ids[qId] = pId;
    } else {
        ids[qId] = pId;
        ranks[pId]++;
    }

    N--;
}

实现算法

实现 kruskal 算法时，先将所有边加入最小堆中，每次取出堆顶的元素 ememe_m，然后使用并查集判断边的两个顶点是否连通，如果不连通就将 ememe_m 加入 TTT，重复这个过程直至 |T|=|V|−1|T|=|V|−1|T|=|V|-1，时间复杂度为 O(|E|log|E|)O(|E|log⁡|E|)O(|E|\log |E|)。

复制package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;
import com.zhiyiyo.collection.queue.MinPriorQueue;
import com.zhiyiyo.collection.queue.Queue;
import com.zhiyiyo.collection.tree.UnionFind;

import java.util.stream.Stream;
import java.util.stream.StreamSupport;

public class KruskalMST implements MST {
    private Queue mst;

 public KruskalMST(WeightedGraph graph) {
 mst = new LinkQueue<>();
 UnionFind uf = new UnionFind(graph.V());

 MinPriorQueue pq = new MinPriorQueue<>();
 for (Edge e : graph.edges()) {
 pq.insert(e);
 }

 while (mst.size() < graph.V() - 1 && !pq.isEmpty()) {
 Edge edge = pq.pop();
 int v = edge.either();
 int w = edge.another(v);
 if (!uf.isConnected(v, w)) {
 mst.enqueue(edge);
 uf.union(v, w);
 }
 }
 }

 @Override
 public Iterable edges() {
 return mst;
 }

 @Override
 public double weight() {
 Stream stream = StreamSupport.stream(mst.spliterator(), false);
 return stream.map(Edge::getWeight).reduce(0d, Double::sum);
 }
}

Prim 算法

Prim 算法的思想是初始化最小生成树为一个根节点 0，然后将根节点的所有邻边加入最小堆中，从最小堆中弹出最小的边 ememe_m，如果 ememe_m 不会使得树中出现环，将将其并入树中。每当有新的节点 vvv 被并入树中时，就得将 vvv 的所有邻边加入最小堆中。重复上述过程直到 |T|=|V|−1|T|=|V|−1|T|=|V|-1，时间复杂度为 O(|E|log|E|)O(|E|log⁡|E|)O(|E|\log|E|)。代码如下所示：

复制package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;
import com.zhiyiyo.collection.queue.MinPriorQueue;
import com.zhiyiyo.collection.queue.Queue;

import java.util.stream.Stream;
import java.util.stream.StreamSupport;

/**
 * 延时版本 Prim 算法
 */
public class PrimMST implements MST {
    private boolean[] marked;
    private MinPriorQueue pq;
 private Queue mst;

 public LazyPrimMST(WeightedGraph graph) {
 marked = new boolean[graph.V()];
 pq = new MinPriorQueue<>();
 mst = new LinkQueue<>();

 mark(graph, 0);
 while (mst.size() < graph.V() - 1 && !pq.isEmpty()) {
 Edge edge = pq.pop();
 int v = edge.either();
 int w = edge.another(v);

 // 构成环则舍弃
 if (marked[v] && marked[w]) continue;
 mst.enqueue(edge);

 if (!marked[v]) mark(graph, v);
 else if (!marked[w]) mark(graph, w);
 }
 }

 private void mark(WeightedGraph graph, int v) {
 marked[v] = true;
 for (Edge edge : graph.adj(v)) {
 if (!marked[edge.another(v)]) {
 pq.insert(edge);
 }
 }
 }

 @Override
 public Iterable edges() {
 return mst;
 }

 @Override
 public double weight() {
 Stream stream = StreamSupport.stream(mst.spliterator(), false);
 return stream.map(Edge::getWeight).reduce(0d, Double::sum);
 }
}

由于每次都是把新节点的所有邻边都加到了最小堆中，会引入许多无用的边，所以《算法第四版》中给出了使用索引优先队列实现的即时版 Prim 算法，时间复杂度能达到 O(|E|log|V|)O(|E|log⁡|V|)O(|E|\log |V|)，但是这里写不下了，大家可以自行查阅，以上~~

转载请注明：xuhss » 如何在 Java 中实现最小生成树算法