? 优质资源分享 ?
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| ? Python实战微信订餐小程序 ? | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| ?Python量化交易实战? | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
本章是系列文章的第十一章,主要介绍GPU的编译原理,分析了多核运行过程中的内存分岔和控制流分岔的分析和处理。
本文中的所有内容来自学习DCC888的学习笔记或者自己理解的整理,如需转载请注明出处。周荣华@燧原科技
11.1 什么是GPU
11.1.1 GPU的发展历史
软件控制的VGA帧缓冲区
频繁使用的图形栅格化程序
尝试用硬件来加速这些处理
流水线化的图形处理过程,例如变形,映射,切片,显示等等
工程师开始发现一些过程本身虽然不一样,但实现该功能的硬件是相似的,例如图着色
从单独的图着色API到泛化的API
GPU指令集的诞生→泛化的整数通用处理函数 → 带分支支持的处理函数
一个独立的栅格化处理芯片 + 通用处理芯片
然后栅格化处理芯片又集成到了GPU里面,变成通用处理芯片的一部分
……
11.1.2 计算机组织
传统的SIMD(Single Instruction Multiple Data)和SPMD(Single Program Multiple Data)到GPU的MSIMD(Multiple Single-Instruction Multiple-Data)
11.1.3 编程环境
主流编程环境主要有两种,开源的OpenCL和闭源的C for CUDA,后者是NVIDIA发布的,前者是其他公司组成的联盟发布的。这里主要说CUDA。
异构编程语言:一个能指定不同异构处理器上执行的编程语言。
传统的C编程语言做矩阵操作的例子:
1 void saxpy\_serial(int n, float alpha, float *x, float *y) {
2 for (int i = 0; i < n; i++)
3 y[i] = alpha * x[i] + y[i];
4 }
5 // Invoke the serial function:
6 saxpy\_serial(n, 2.0, x, y);转换成CUDA的例子:
1 \_\_global\_\_ void saxpy\_parallel(int n, float alpha, float *x, float *y) {
2 int i = blockIdx.x * blockDim.x + threadIdx.x;
3 if (i < n)
4 y[i] = alpha * x[i] + y[i];
5 }
6 // Invoke the parallel kernel:
7 int nblocks = (n + 255) / 256;
8 saxpy\_parallel<<256>>>(n, 2.0, x, y);NV的GPU的组织结构:Grids → Blocks → Warps → Threads
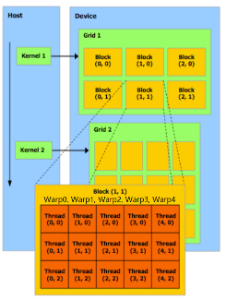
Cuda programs = CPU programs + kernels
Kernels调用语法:
kernel<<>>(A,B,w,C);指定grids和block
CPU programs → host programs
kernels → PTX (Parallel Thread Execution) → SASS (Streaming ASSembly)
11.2 分岔(Divergence)
英文里面Divergence有分岔,分支,歧义等多种意思,这里表示程序执行到某个点之后,可能有多个分支的情况。
11.2.1 SIMD的优缺点
优点:更低的功耗,指令解码占用空间更少。
对于没有分支的线性程序,SIMD的性能非常好。但程序几乎不可避免会存在多个分支。
常见的分支主要有两类:
- 因为内存访问地址不一致导致的内存分岔
- 因为控制流分支导致的分岔
11.2.2 控制流分岔的例子
对下面的cuda 代码:
1 \_\_global\_\_ void ex(float *v) {
2 if (v[tid] < 0.0) {
3 v[tid] /= 2;
4 } else {
5 v[tid] = 0.0;
6 }
7 }对应的控制流图是这样的:
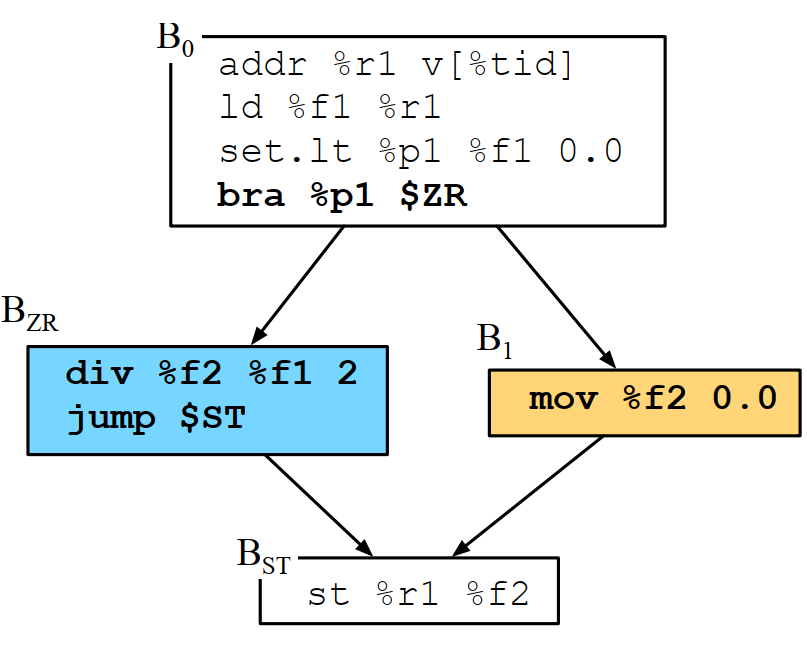
因为上面程序只有一处分岔(还记得上一章ILP中说的超级块么?上面的DAG转换成树之后只有2个叶子节点),如果有两个ALU,我们就可以在无视分岔的情况下把程序执行流水线画出来:
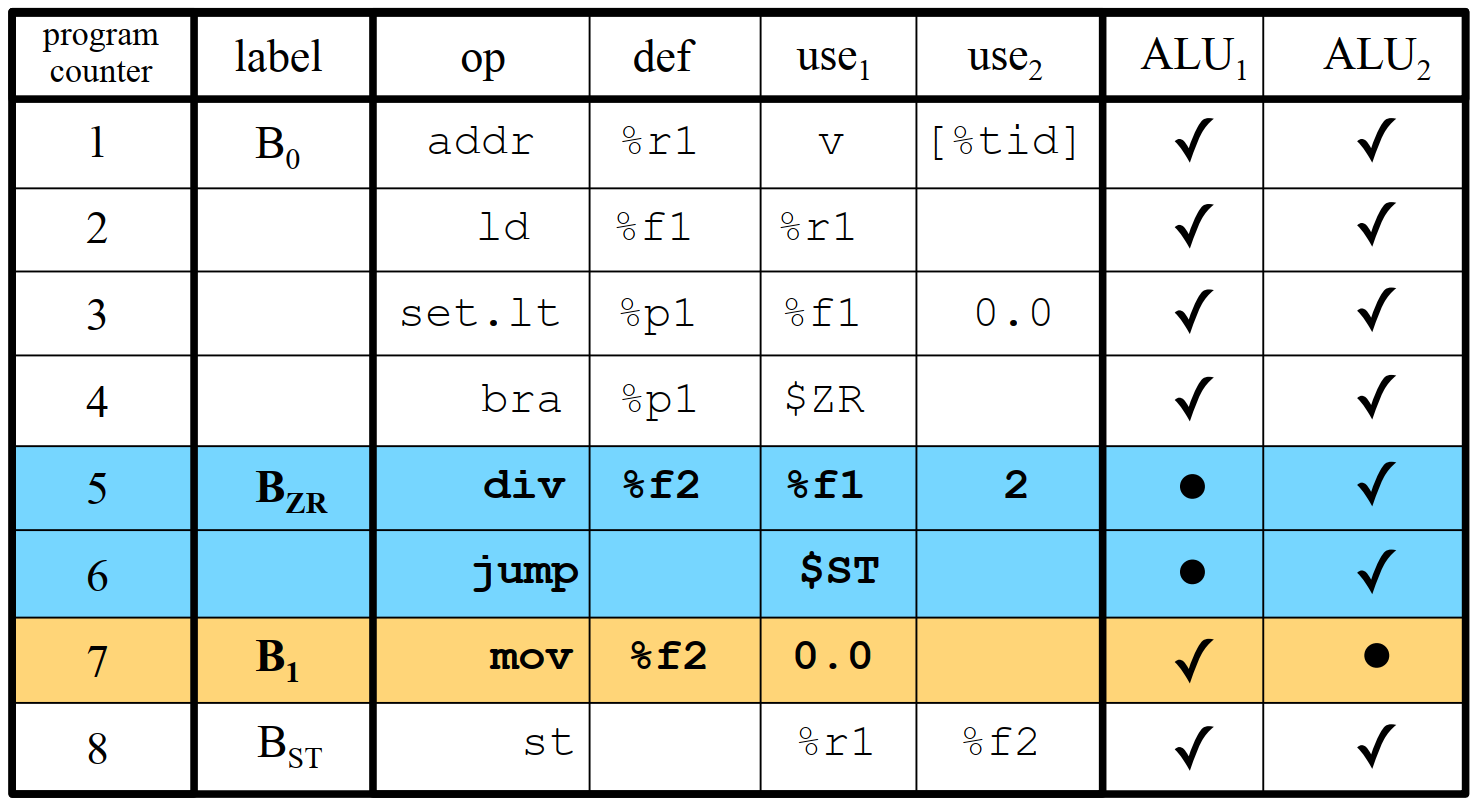
11.2.3 什么样的输入性能最好?
对下面的cuda的例子,怎么样调整输入来达到最好的性能?
1 \_\_global\_\_ void dec2zero(int *v, int N) {
2 int xIndex = blockIdx.x * blockDim.x + threadIdx.x;
3 if (xIndex < N) {
4 while (v[xIndex] > 0) {
5 v[xIndex]--;
6 }
7 }
8 }下面有五种初始化的方法:
1 void vecIncInit(int *data, int size) {
2 for (int i = 0; i < size; ++i) {
3 data[i] = size - i - 1;
4 }
5 }
6 void vecConsInit(int *data, int size) {
7 int cons = size / 2;
8 for (int i = 0; i < size; ++i) {
9 data[i] = cons;
10 }
11 }
12 void vecAltInit(int *data, int size) {
13 for (int i = 0; i < size; ++i) {
14 if (i % 2) {
15 data[i] = size;
16 }
17 }
18 }
19 void vecRandomInit(int *data, int size) {
20 for (int i = 0; i < size; ++i) {
21 data[i] = random() % size;
22 }
23 }
24 void vecHalfInit(int *data, int size) {
25 for (int i = 0; i < size / 2; ++i) {
26 data[i] = 0;
27 }
28 for (int i = size / 2; i < size; ++i) {
29 data[i] = size;
30 }
31 }测试下来的结果,在总的执行近似的情况下,没有分岔和有一个分岔的性能是2倍的差异,正好印证了之前一个分岔需要2个ALU才能确保并行处理的观点。另外一个分岔的性能和另外触发了一个随机数生成器调用的性能接近:
| |
vecIncInit| vecConsInit |
vecAltInit|
vecRandomInit|
vecHalfInit| 总时间 | 20480000 | 20480000 | 20476800 | 20294984 | 20480000 |
| 实际时间 | 16250 | 16153 | 32193 | 30210 | 16157 |
11.3 分岔的动态检测
11.3.1 分岔profiling
统计分岔执行时间和执行次数的方法
在并行世界,求程序的profile的过程远比单核世界复杂,因为需要一个算法找到那时正在运行的线程将这个profile的结果保存下来。
下面是常见的找记录者的算法:
1 int writer = 0;
2 bool gotWriter = false;
3 while (!gotWriter) {
4 bool iAmWriter = false;
5 if (laneid == writer) {
6 iAmWriter = true;
7 }
8 if ( ∃ t ∈ w | iAmWriter == true) {
9 gotWriter = true;
10 }
11 else {
12 writer++;
13 }
14 }11.3.2 经典的双调排序Bitonic Sort
输入是乱序3/2/4/1,经过5次排序和4次交换之后,变成顺序的1/2/3/4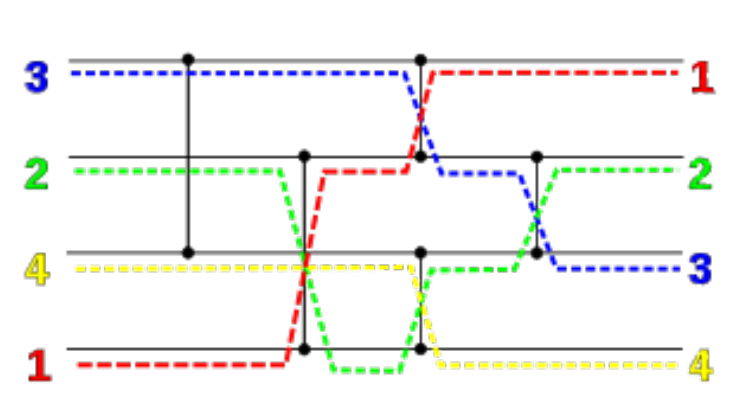
双调排序的cuda代码如下:
1 \_\_global\_\_ static void bitonicSort(int *values) {
2 extern \_\_shared\_\_ int shared[];
3 const unsigned int tid = threadIdx.x;
4 shared[tid] = values[tid];
5 \_\_syncthreads();
6 for (unsigned int k = 2; k <= NUM; k *= 2) {
7 for (unsigned int j = k / 2; j > 0; j /= 2) {
8 unsigned int ixj = tid ^ j;
9 if (ixj > tid) {
10 if ((tid & k) == 0) {
11 if (shared[tid] > shared[ixj]) {
12 swap(shared[tid], shared[ixj]);
13 }
14 } else {
15 if (shared[tid] < shared[ixj]) {
16 swap(shared[tid], shared[ixj]);
17 }
18 }
19 }
20 \_\_syncthreads();
21 }
22 }
23 values[tid] = shared[tid];
24 }我们先不看外面的for循环,针对核心的8到20行生成控制流图:
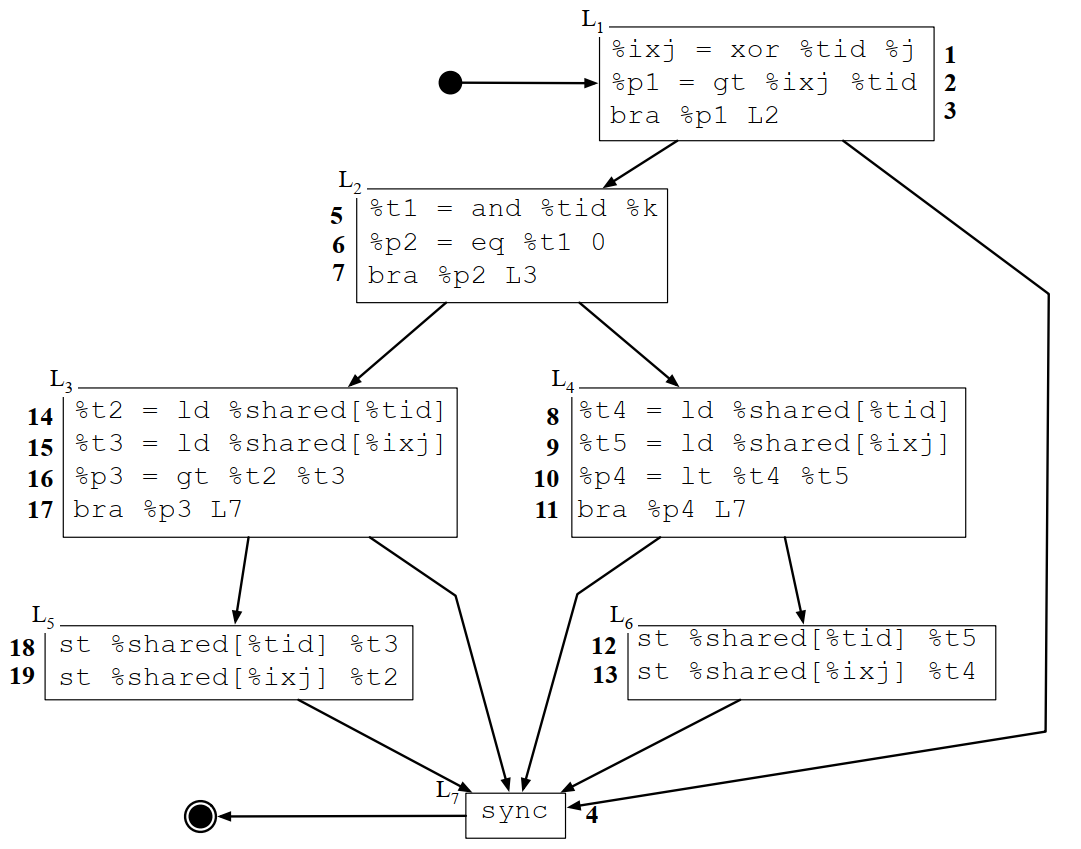
如果对执行过程做一下trace,大概结果是这样(上面代码里面有4个if,所以转换成DAG之后就有4个分岔,对应执行时的4个线程):
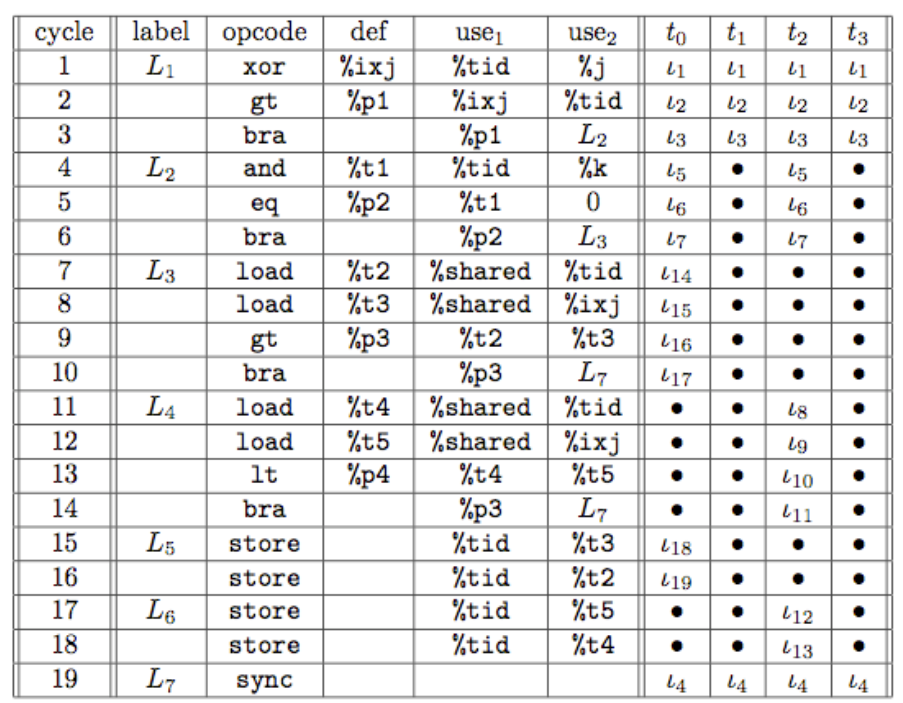
第一轮优化,3个分岔变成2个:
1 unsigned int a, b;
2 if ((tid & k) == 0) {
3 b = tid;
4 a = ixj;
5 } else {
6 b = ixj;
7 a = tid;
8 }
9 if (sh[b] > sh[a]) {
10 swap(sh[b], sh[a]);
11 }优化之后的控制流图变成这样(性能提升6.7%):
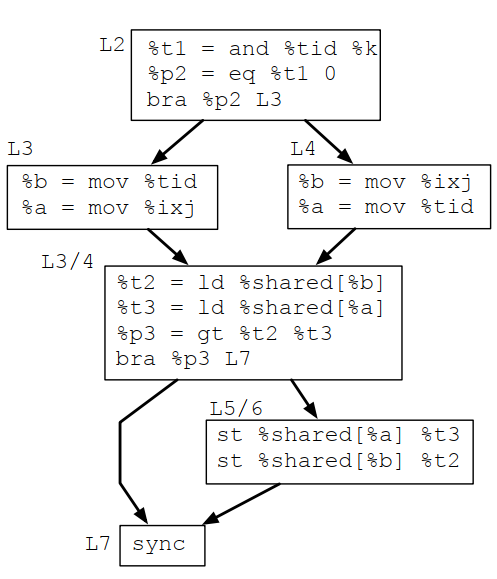
第二轮优化,2个分岔变成1个:
1 int p = (tid & k) == 0;
2 unsigned b = p ? tid : ixj;
3 unsigned a = p ? ixj : tid;
4 if (sh[b] > sh[a]) {
5 swap(sh[b], sh[a]);
6 }实际上?表达式也是完成分岔的功能,但由于大多数指令集都有专门的问号表达式的指令,所以巧妙使用问号表达式将第一重分岔消掉,改进之后的CFG是这样的(性能提升9.2%):
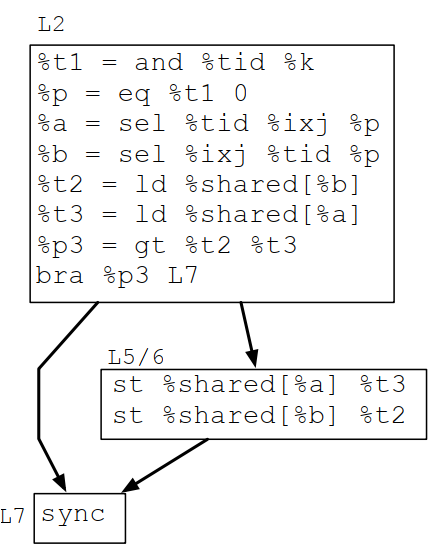
11.3.3 总结
性能优化过程主要是消灭分岔,那前面提到的profile数据对这个性能优化有帮助么?
理论上不论profile数据是什么样的,能消灭的分岔肯定优先消灭掉。profile数据对分岔消除的提示是尽可能优先消除执行时间比较长,执行次数比较多的分岔。
抛开分岔问题本身,profile的数据会提示优化执行时间和执行次数比较多的BB。
11.4 分岔的静态检测
11.4.1 分岔变量和统一变量
分岔变量(Divergent Variables):如果一个变量对不同线程会出现不同的值,则称该变量为分岔变量。
统一变量(Uniform Variables):如果一个变量在不同线程呈现完全相同的值,则称该变量为统一变量。
成为分岔变量的几种场景:
- tid是分岔变量
- 原子操作产生的变量是分岔变量
- 如果v对分岔变量有数据依赖,则v也是分岔变量
- 如果v对分岔变量有控制依赖,则v也是分岔变量
分岔变量在数据流图和控制流图上具有传播性。
11.4.2 找到依赖
在一个非SSA的程序里面,找到某个变量是分岔变量还是非分岔变量是有歧义的,因为一个变量被多次赋值,可能有些赋值生成统一变量,有些赋值生成分岔变量。
但在SSA格式程序中,变量的分岔属性值就要容易确定的多。
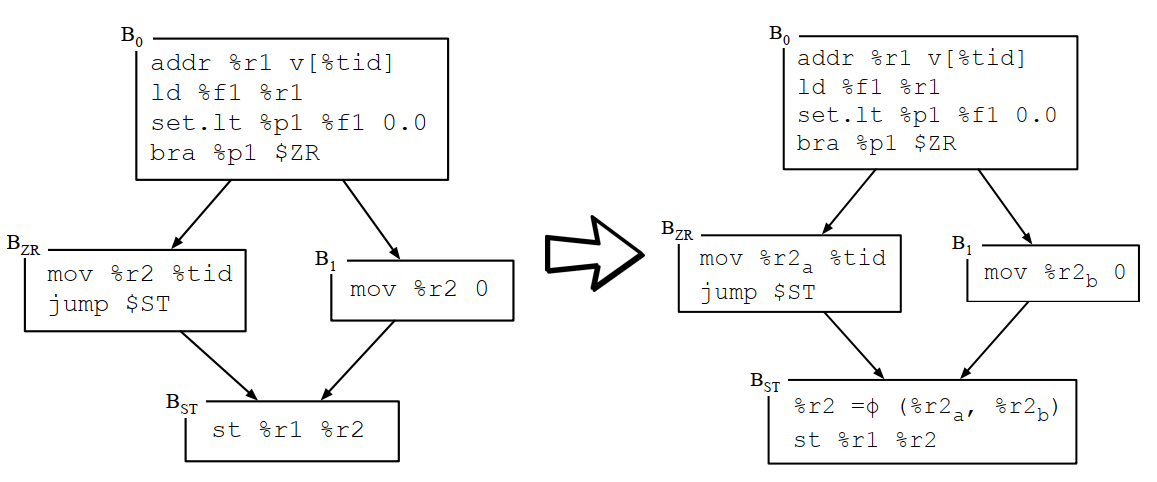
例如下面的例子中r2在未SSA化之前,可能是分岔变量,也可能是统一变量。右边SSA化之后,r2a和r2是分岔变量,r2b是统一变量。
11.4.3 数据依赖图DDG
在ILP里面,我们曾经说过IDG,指令依赖图,这里说的数据依赖图和IDG其实也是类似的,关注的都是数据依赖,不过IDG关注的是指令执行过程的依赖,DDG关注的是数据本身的依赖。
对下面的CFG,会生成什么样的DDG?
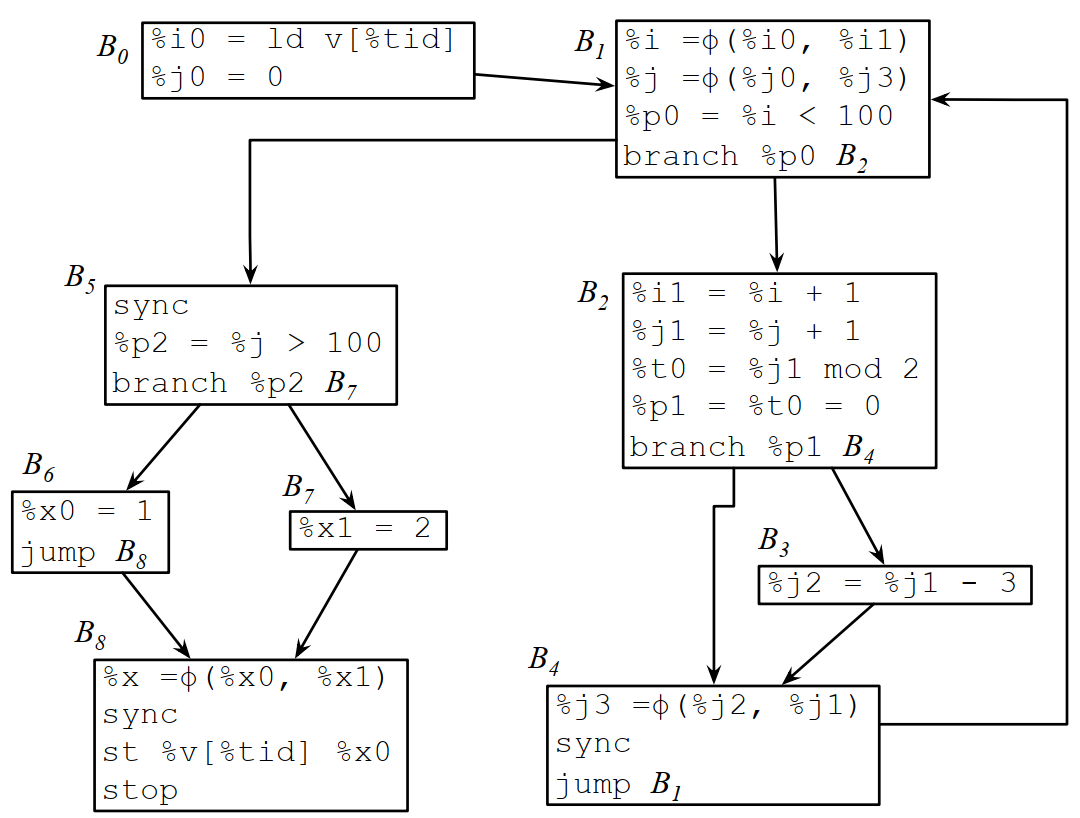
对应的DDG如下:
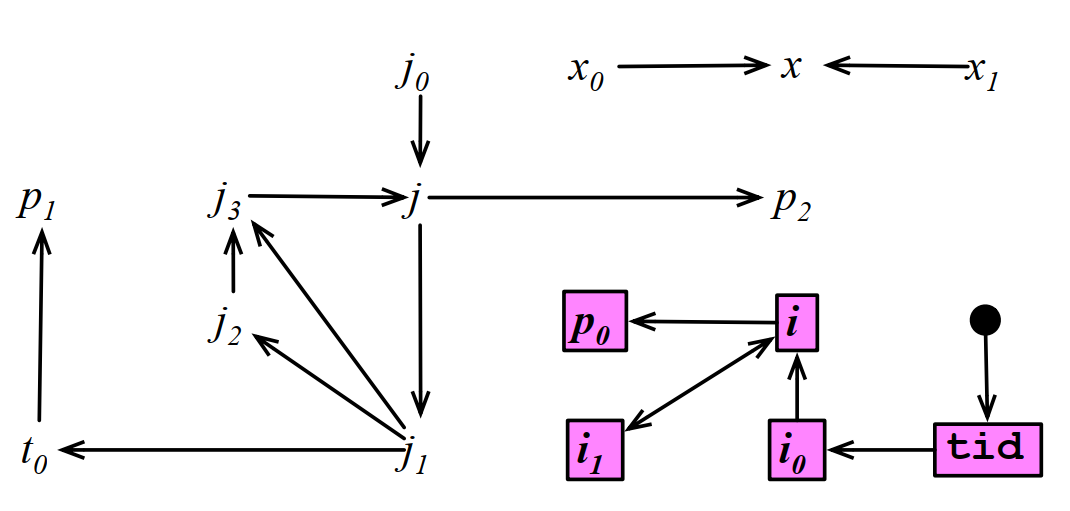
这个数据依赖对ILP可能已经足够了,但对分岔分析还不够,有些分岔变量漏掉了!
例如j的值依赖B1里面的分支,这个分支的条件是个分岔变量,这也会导致j变成分岔变量。所以除了数据依赖外,还需要考虑控制依赖。
11.4.4 控制依赖图
影响区:一个分支断言的影响区是该断言影响的基本块的集合。
后支配:相对于支配属性而言,后支配属性是一个节点B2走到程序结束的每条路径都要经过B1,则称为B1后支配B2。
直接后支配:如果节点B1后支配节点B2,并且不存在一个节点B3,B1后支配B3,并且B3后支配B2,则称为B1是B2的直接后支配。
一个分支断言的影响区是该分支所在BB到分支的直接后支配BB。
为了方便表示控制依赖导致的后支配,我们将φ函数升级扩展成为带断言的φ函数。例如下图中的x本来只对x0和x1有数据依赖,现在它也对p2有数据依赖:
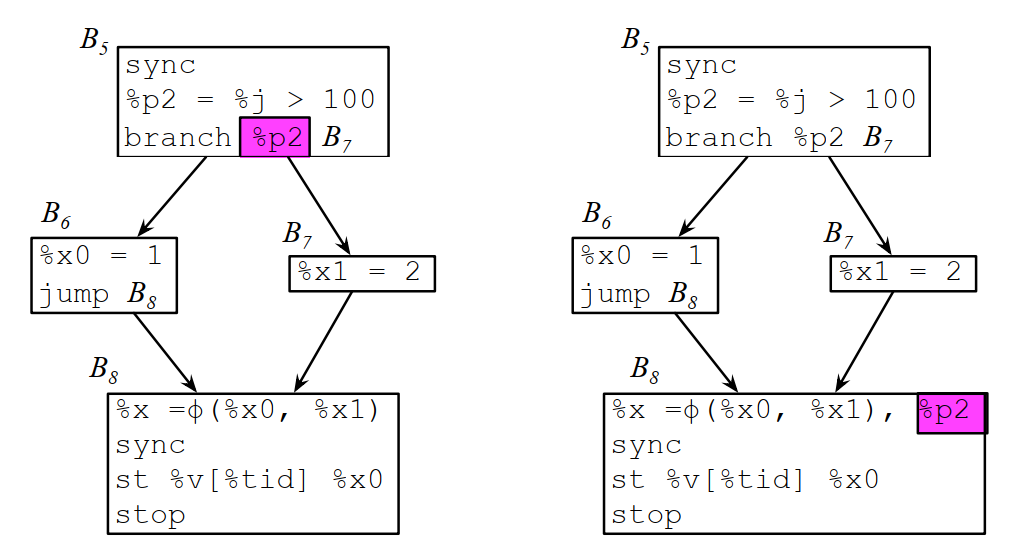
升级φ函数之后的数据依赖图:
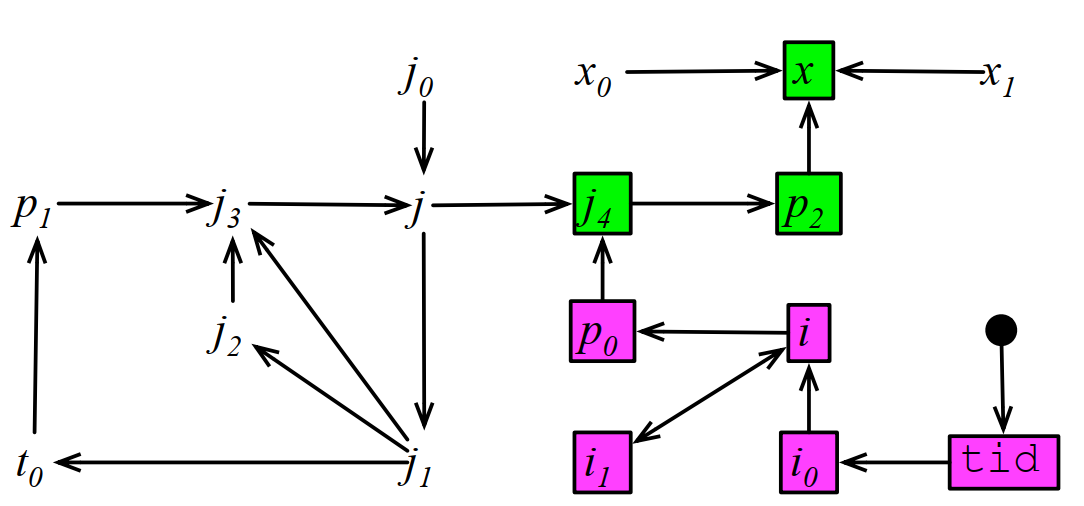
11.5 分岔优化
11.5.1 同步栅栏删除
CUDA的ptx指令集默认分支命令都是会产生分岔的,除非特定加上.uni后缀:

所以在明确肯定不会产生分岔变量的分支命令,可以加上.uni后缀:

上面的截图来自PTX ISA :: CUDA Toolkit Documentation (nvidia.com)
11.5.2 寄存器分配
相对于传统单核的寄存器分配,溢出处理都是直接放到内存中,GPU场景下的寄存器溢出可以选择溢出老本地内存和全局内存,部分在多个核中共享的变量,还可以考虑放到共享内存中。
11.5.3 数据重定位
准排序算法
将数据切片,每个线程处理一个切片,并在每个切片排序完之后,再拷贝回来:
1 \_\_global\_\_ static void maxSort1(int *values, int N) {
2 // 1) COPY-INTO: Copy data from the values vector
3 // into shared memory:
4 \_\_shared\_\_ int shared[THREAD\_WORK\_SIZE * NUM\_THREADS];
5 for (unsigned k = 0; k < THREAD\_WORK\_SIZE; k++) {
6 unsigned loc = k * blockDim.x + threadIdx.x;
7 if (loc < N) {
8 shared[loc] = values[loc + blockIdx.x * blockDim.x];
9 }
10 }
11 \_\_syncthreads();
12 // 2) SORT: each thread sorts its chunk of data
13 // with a small sorting net.
14 int index1 = threadIdx.x * THREAD\_WORK\_SIZE;
15 int index2 = threadIdx.x * THREAD\_WORK\_SIZE + 1;
16 int index3 = threadIdx.x * THREAD\_WORK\_SIZE + 2;
17 int index4 = threadIdx.x * THREAD\_WORK\_SIZE + 3;
18 if (index4 < N) {
19 swapIfNecessary(shared, index1, index3);
20 swapIfNecessary(shared, index2, index4);
21 swapIfNecessary(shared, index1, index2);
22 swapIfNecessary(shared, index3, index4);
23 swapIfNecessary(shared, index2, index3);
24 }
25 \_\_syncthreads();
26 // 3) SCATTER: the threads distribute their data
27 // along the array.
28 \_\_shared\_\_ int scattered[THREAD\_WORK\_SIZE * 300];
29 unsigned int nextLoc = threadIdx.x;
30 for (unsigned i = 0; i < THREAD\_WORK\_SIZE; i++) {
31 scattered[nextLoc] = shared[threadIdx.x * THREAD\_WORK\_SIZE + i];
32 nextLoc += blockDim.x;
33 }
34 \_\_syncthreads();
35 // 4) COPY-BACK: Copy the data back from the shared
36 // memory into the values vector:
37 for (unsigned k = 0; k < THREAD\_WORK\_SIZE; k++) {
38 unsigned loc = k * blockDim.x + threadIdx.x;
39 if (loc < N) {
40 values[loc + blockIdx.x * blockDim.x] = scattered[loc];
41 }
42 }
43 }11.6 分岔研究历史
GPU的历史都比较新,所以关于GPU的分岔分析资料也比较新:
- Ryoo, S. Rodrigues, C. Baghsorkhi, S. Stone, S. Kirk, D. and Hwu, Wen-Mei. "Optimization principles and application performance evaluation of a multithreaded GPU using CUDA", PPoPP, p 73-82 (2008) CUDA介绍
- Coutinho, B. Diogo, S. Pereira, F and Meira, W. "Divergence Analysis and Optimizations", PACT, p 320-329 (2011) 分岔分析与优化
- Sampaio, D. Martins, R. Collange, S. and Pereira, F. "Divergence Analysis", TOPLAS, 2013. 分岔分析
转载请注明:xuhss » 程序分析与优化 – 11 多分支分析